Bài 7.24 trang 56 SGK Toán 10 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.24 trang 56 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km.
Đề bài
Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km. Tại cùng mộtthời điểm, hai trạm cùng phát tín hiệu với vận tốc 292 000 km/s để một tàu thuỷ thu và đo độ lệch thời gian. Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s. Từ thông tin trên, ta có thể xác định được tàu thuỷ thuộc đường hypebol nào? Viết phương trình chính tắc của hypebol đó theo đơn vị kilômét.
Phương pháp giải - Xem chi tiết
Gắn hệ trục tọa độ, sau đó tìm phương trình hyperbol đi qua vị trí tàu thủy.
Lời giải chi tiết
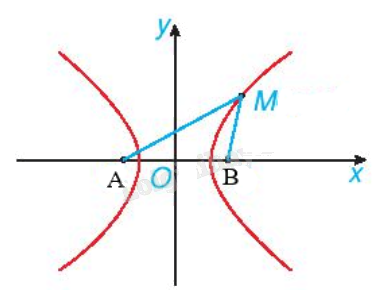
Gọi M là vị trí tàu thu tín hiệu. Gọi \({t_A},{t_B}\) lần lượt là thời gian tín hiệu truyền từ trạm phát A, B đến M. Theo đề bài, ta có \({t_A} - {t_B} = - 0,0005s\).
Suy ra \(MA - MB = v.{t_A} - v.{t_B} = 292000.\left( { - 0,0005} \right) = - 146km\).
Gọi (H) là hyperbol ở dạng chính tắc nhận A, B làm hai tiêu điểm và đi qua M. Khi đó ta có:
\(\left\{ \begin{array}{l}2a = \left| {MA - MB} \right| = 146\\2c = AB = 300\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\c = 150\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\{b^2} = {c^2} - {a^2} = 17171\end{array} \right.\)
Vậy phương trình chính tắc của (H) là: \(\frac{{{x^2}}}{{5329}} - \frac{{{y^2}}}{{17171}} = 1\).
Bài 7.24 trang 56 SGK Toán 10 – Kết nối tri thức là một bài toán ứng dụng kiến thức về vectơ trong hình học. Để giải bài toán này, học sinh cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ và cách sử dụng vectơ để biểu diễn các yếu tố hình học.
Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ AM theo hai vectơ AB và AC.
Để tìm vectơ AM theo hai vectơ AB và AC, ta sử dụng tính chất trung điểm của đoạn thẳng BC.
Vì M là trung điểm của BC, ta có: BM = MC. Do đó, BC = 2BM.
Ta có: AM = AB + BM. Mà BM = (1/2)BC. Vậy AM = AB + (1/2)BC.
Tiếp theo, ta biểu diễn BC qua AB và AC. Ta có: BC = AC - AB.
Thay BC = AC - AB vào biểu thức AM = AB + (1/2)BC, ta được:
AM = AB + (1/2)(AC - AB) = AB + (1/2)AC - (1/2)AB = (1/2)AB + (1/2)AC
Vậy, AM = (1/2)AB + (1/2)AC.
Để hiểu rõ hơn về cách giải các bài tập liên quan đến vectơ, các em có thể tham khảo các bài tập tương tự sau:
Bài 7.24 trang 56 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!