Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 1 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 3 trang 40 và 41 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, logic và dễ tiếp thu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giải tam giác ABC, biết b = 32, c =45, A =87. Từ một khu vực có thể quan sát được hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.
Giải tam giác ABC, biết b = 32, c =45, \(\widehat A = {87^o}\)
Phương pháp giải:
Tính độ dài các cạnh và các góc còn lại của tam giác.
Bước 1: Tính a: \({a^2} = {b^2} + {c^2} - 2.bc.\cos A\)
Bước 2: Tính sinB, suy ra góc B, góc C.
Lời giải chi tiết:
Ta cần tính cạnh BC, góc B và góc C.
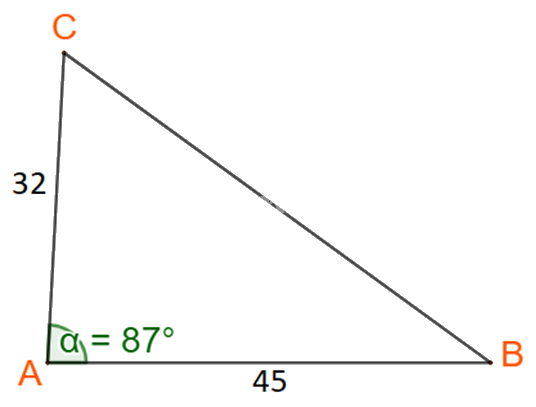
Áp dụng định lí cosin tại đỉnh A ta có:
\({a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = {32^2} + {45^2} - 2.32.45.\cos {87^o}\\ \Leftrightarrow B{C^2} \approx 2898,27\\ \Leftrightarrow BC \approx 53,8\end{array}\)
Theo định lí sin, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \Rightarrow \sin B = \frac{{b.\sin A}}{a} = \frac{{32.\sin {{87}^o}}}{{53,8}} \approx 0,594.\)
\( \Rightarrow \widehat B \approx 36,{44^o}\) hoặc \(\widehat B \approx 143,{56^o}\)(Loại vì \(\widehat A + \widehat B = 230,{56^o} > {180^o}\))
\( \Rightarrow \widehat C = {180^o} - \widehat A - \widehat B \approx {180^o} - {87^o} - 36,{44^o} = 56,{56^o}\)
Vậy tam giác ABC có \(BC \approx 53,8\); \(\widehat B \approx 36,{44^o}\) và \(\widehat C = 56,{56^o}\).
Từ một khu vực có thể quan sát được hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.
Phương pháp giải:
Bước 1: Cố định vị trí đứng ngắm, xác định góc ngắm .
Bước 2: Đo khoảng cách từ vị trí ngắm tới từng đỉnh núi..
Bước 3: Áp dụng định lí cosin để xác định khoảng cách giữa hai đỉnh núi.
Lời giải chi tiết:
Bước 1: Tại khu vực quan sát, đặt một cọc tiêu cố định tại vị trí A. Kí hiệu hai đỉnh núi lần lượt là điểm B và điểm C.
+) Đứng tại A, ngắm điểm B và điểm C để đo góc tạo bởi hai hướng ngắm đó.
Bước 2: Đo khoảng cách từ vị trí ngắm đến từng đỉnh núi, tức là tính AB, AC.
+) Đứng tại A, ngắm đỉnh núi B để xác định góc ngắm so với mặt đất, kí hiệu là góc \(\alpha \).
+) Theo hướng ngắm, đặt tiếp cọc tiêu tại D gần đỉnh núi hơn và đo đoạn AD. Xác định góc ngắm tại điểm D, kí hiệu là góc\(\beta \)
Hình vẽ:
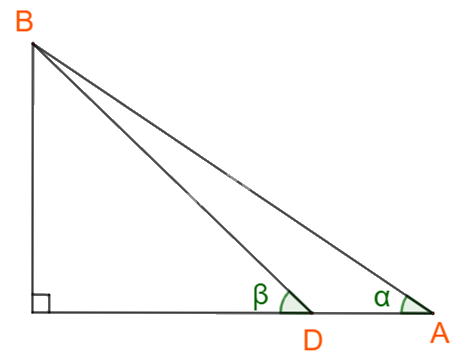
Dễ dàng tính được góc \(\widehat {DBA} = {180^o} - \alpha - \beta .\)
Áp dụng định lí sin cho tam giác ABD ta được: \(\frac{{AB}}{{\sin D}} = \frac{{DA}}{{\sin B}} \Rightarrow AB = \sin D.\frac{{DA}}{{\sin B}} = \sin \left( {{{180}^o} - \beta } \right).\frac{{DA}}{{\sin \left( {{{180}^o} - \alpha - \beta } \right)}}.\)
Bước 3: Tính khoảng cách giữa hai đỉnh núi, bằng cách áp dụng định lí cosin cho tam giác ABC để tính độ dài cạnh BC.
Giải tam giác ABC, biết b = 32, c =45, \(\widehat A = {87^o}\)
Phương pháp giải:
Tính độ dài các cạnh và các góc còn lại của tam giác.
Bước 1: Tính a: \({a^2} = {b^2} + {c^2} - 2.bc.\cos A\)
Bước 2: Tính sinB, suy ra góc B, góc C.
Lời giải chi tiết:
Ta cần tính cạnh BC, góc B và góc C.
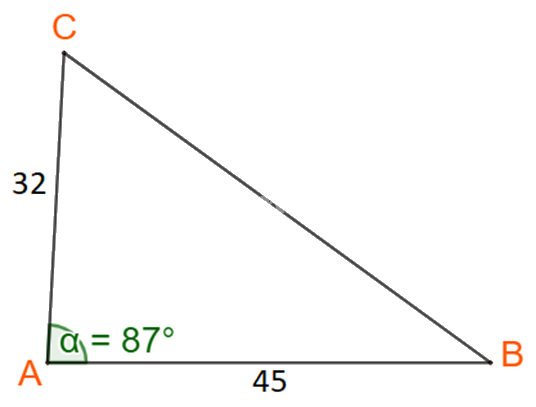
Áp dụng định lí cosin tại đỉnh A ta có:
\({a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = {32^2} + {45^2} - 2.32.45.\cos {87^o}\\ \Leftrightarrow B{C^2} \approx 2898,27\\ \Leftrightarrow BC \approx 53,8\end{array}\)
Theo định lí sin, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \Rightarrow \sin B = \frac{{b.\sin A}}{a} = \frac{{32.\sin {{87}^o}}}{{53,8}} \approx 0,594.\)
\( \Rightarrow \widehat B \approx 36,{44^o}\) hoặc \(\widehat B \approx 143,{56^o}\)(Loại vì \(\widehat A + \widehat B = 230,{56^o} > {180^o}\))
\( \Rightarrow \widehat C = {180^o} - \widehat A - \widehat B \approx {180^o} - {87^o} - 36,{44^o} = 56,{56^o}\)
Vậy tam giác ABC có \(BC \approx 53,8\); \(\widehat B \approx 36,{44^o}\) và \(\widehat C = 56,{56^o}\).
Từ một khu vực có thể quan sát được hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.
Phương pháp giải:
Bước 1: Cố định vị trí đứng ngắm, xác định góc ngắm .
Bước 2: Đo khoảng cách từ vị trí ngắm tới từng đỉnh núi..
Bước 3: Áp dụng định lí cosin để xác định khoảng cách giữa hai đỉnh núi.
Lời giải chi tiết:
Bước 1: Tại khu vực quan sát, đặt một cọc tiêu cố định tại vị trí A. Kí hiệu hai đỉnh núi lần lượt là điểm B và điểm C.
+) Đứng tại A, ngắm điểm B và điểm C để đo góc tạo bởi hai hướng ngắm đó.
Bước 2: Đo khoảng cách từ vị trí ngắm đến từng đỉnh núi, tức là tính AB, AC.
+) Đứng tại A, ngắm đỉnh núi B để xác định góc ngắm so với mặt đất, kí hiệu là góc \(\alpha \).
+) Theo hướng ngắm, đặt tiếp cọc tiêu tại D gần đỉnh núi hơn và đo đoạn AD. Xác định góc ngắm tại điểm D, kí hiệu là góc\(\beta \)
Hình vẽ:
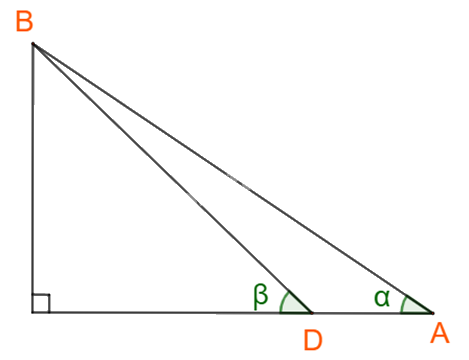
Dễ dàng tính được góc \(\widehat {DBA} = {180^o} - \alpha - \beta .\)
Áp dụng định lí sin cho tam giác ABD ta được: \(\frac{{AB}}{{\sin D}} = \frac{{DA}}{{\sin B}} \Rightarrow AB = \sin D.\frac{{DA}}{{\sin B}} = \sin \left( {{{180}^o} - \beta } \right).\frac{{DA}}{{\sin \left( {{{180}^o} - \alpha - \beta } \right)}}.\)
Bước 3: Tính khoảng cách giữa hai đỉnh núi, bằng cách áp dụng định lí cosin cho tam giác ABC để tính độ dài cạnh BC.
Mục 3 trong SGK Toán 10 tập 1 - Kết nối tri thức tập trung vào các khái niệm và ứng dụng của vectơ trong mặt phẳng. Các bài tập trang 40 và 41 thường xoay quanh việc xác định, biểu diễn vectơ, thực hiện các phép toán vectơ (cộng, trừ, nhân với một số thực) và ứng dụng chúng để giải quyết các bài toán hình học cơ bản.
Bài 3.1 thường yêu cầu học sinh xác định các vectơ trong hình vẽ, chỉ ra các vectơ cùng phương, ngược phương, bằng nhau. Để giải bài này, cần nắm vững định nghĩa về vectơ, các khái niệm về phương, chiều, độ dài của vectơ.
Ví dụ:
Bài 3.2 thường liên quan đến việc thực hiện các phép toán cộng, trừ vectơ. Cần áp dụng quy tắc cộng, trừ vectơ theo hình bình hành hoặc quy tắc tam giác.
Ví dụ:
Cho hai vectơ a và b. Tìm vectơ a + b và a - b.
Bài 3.3 thường yêu cầu học sinh chứng minh đẳng thức vectơ. Để giải bài này, cần sử dụng các quy tắc cộng, trừ vectơ, quy tắc nhân vectơ với một số thực và các tính chất của phép toán vectơ.
Ví dụ:
Chứng minh rằng: a + (b + c) = (a + b) + c
Bài 3.4 thường là các bài toán ứng dụng vectơ để giải quyết các bài toán hình học. Cần phân tích hình vẽ, xác định các vectơ liên quan và sử dụng các phép toán vectơ để tìm ra kết quả.
Ví dụ:
Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: 2MA = AB + AC
Học Toán đòi hỏi sự kiên trì và luyện tập thường xuyên. Đừng ngại hỏi thầy cô hoặc bạn bè khi gặp khó khăn. Hãy tìm hiểu kỹ lý thuyết trước khi làm bài tập. Sử dụng các nguồn tài liệu tham khảo khác nhau để mở rộng kiến thức. Chúc bạn học tốt!
| Công thức | Mô tả |
|---|---|
| a + b = b + a | Tính giao hoán của phép cộng vectơ |
| a + (b + c) = (a + b) + c | Tính kết hợp của phép cộng vectơ |
| k(a + b) = ka + kb | Tính chất phân phối của phép nhân vectơ với một số thực |