Bài 4.20 trang 65 SGK Toán 10 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng của vectơ trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.20 trang 65 SGK Toán 10 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
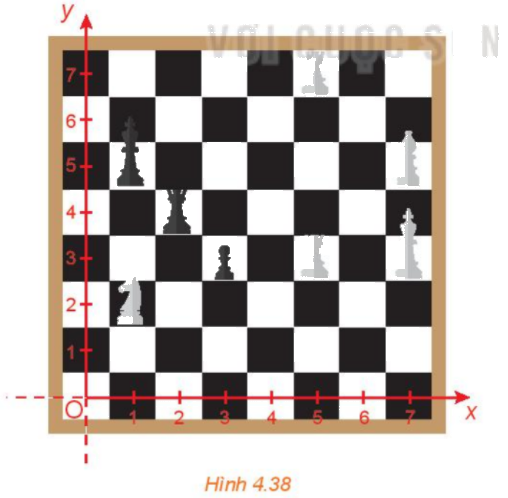
Trong hình 4.38, quân mã đang ở vị trí có tọa độ (1; 2). Hỏi sau một nước đi, quân mã có thể đến những vị trí nào?
Đề bài
Trong hình 4.38, quân mã đang ở vị trí có tọa độ (1; 2). Hỏi sau một nước đi, quân mã có thể đến những vị trí nào?
Phương pháp giải - Xem chi tiết
+) Quân mã đi theo đường chéo hình chữ nhật dài 3 ô, rộng 2 ô.
Bước 1: Đánh dấu các vị trí trên bàn cờ mà quân mã có thể đi ở nước cờ tiếp theo.
Bước 2: Chiếu vuông góc xuống các trục Ox, Oy để xác định tọa độ.
Lời giải chi tiết
a) Quân mã đi theo đường chéo hình chữ nhật có chiều dài 3 ô, chiều rộng 2 ô.
Do đó, từ vị trí hiện tại, quân mã có thể đi đến các vị trí A, B, C, D, E, F như dưới đây:
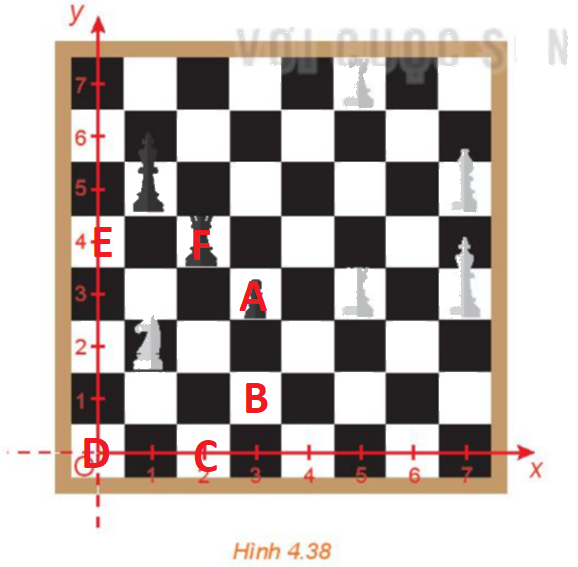
A có tọa độ (3; 3)
B có tọa độ (3; 1)
C có tọa độ (2; 0)
D có tọa độ (0; 0)
E có tọa độ (0; 4)
F có tọa độ (2; 4)
Vậy quân mã có thể đi đến các vị trí A(3;3), B(3;1), C(2;0), D(0;0), E(0;4), F(2;4).
Bài 4.20 trang 65 SGK Toán 10 tập 1 – Kết nối tri thức là một bài toán ứng dụng kiến thức về vectơ trong hình học, cụ thể là việc sử dụng vectơ để chứng minh các tính chất hình học. Để giải bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ (cộng, trừ, nhân với một số thực) và các tính chất của vectơ.
(Nội dung đề bài sẽ được chèn vào đây. Ví dụ: Cho hình bình hành ABCD. Gọi M là trung điểm của BC. Gọi N là giao điểm của AM và BD. Chứng minh rằng: a) AN = 3/4 AM; b) BN = 1/4 BD.)
Để giải bài toán này, chúng ta sẽ sử dụng phương pháp vectơ. Dưới đây là các bước giải chi tiết:
Ví dụ minh họa (giả sử đề bài như trên):
Giả sử A(0;0), B(a;0), C(a+b;c), D(b;c). Khi đó:
Vì N là giao điểm của AM và BD, nên tồn tại số k sao cho $\vec{AN} = k\vec{AM}$. Đồng thời, $\vec{BN} = t\vec{BD}$ (với t là một số thực). Từ đó, ta có thể tìm ra giá trị của k và t để chứng minh các đẳng thức $\vec{AN} = \frac{3}{4}\vec{AM}$ và $\vec{BN} = \frac{1}{4}\vec{BD}$.
Để củng cố kiến thức về vectơ và ứng dụng của vectơ trong hình học, các em học sinh có thể tham khảo thêm các bài tập tương tự trong SGK Toán 10 tập 1 – Kết nối tri thức và các tài liệu luyện tập khác.
Bài 4.20 trang 65 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng của vectơ trong hình học. Hy vọng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin giải bài tập này và các bài tập tương tự một cách hiệu quả.