Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 28, 29, 30 sách giáo khoa Toán 10 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Xét biểu thức F(x, y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Toạ độ ba đình là O(0, 0), A(150, 0) và B(0; 150) (H.2.5). Một cửa hàng có kế hoạch nhập về hai loại máy tính A và B, giá mỗi chiếc lần lượt là 10 triệu đồng và 20 triệu đồng với số vốn ban đầu không vượt quá 4 tỉ đồng.
Một cửa hàng có kế hoạch nhập về hai loại máy tính A và B, giá mỗi chiếc lần lượt là 10 triệu đồng và 20 triệu đồng với số vốn ban đầu không vượt quá 4 tỉ đồng. Loại máy A mang lại lợi nhuận 2,5 triệu đồng cho mỗi máy bán được và loại máy B mang lại lợi nhuận là 4 triệu đồng mỗi máy. Cửa hàng ước tính rằng tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy. Giả sử trong một tháng cửa hàng cần nhập số máy tính loại A là x và số máy tính loại B là y.
a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương
trình rồi xác định miền nghiệm của hệ đó.
b) Gọi F (triệu đồng) là lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B. Hãy biểu diễn F theo x và y.
c) Tìm số lượng máy tính mỗi loại cửa hàng cần nhập về trong tháng đó đề lợi nhuận thu được là lớn nhất.
Phương pháp giải:
a)
Bước 1: Lập bảng thể hiện vốn và lợi nhuận của mỗi loại máy.
Bước 2: Dựa vào các điều kiện sau để lập bất phương trình:
+ Số lượng là số tự nhiên
+ Điều kiện vốn ban đầu
+ Nhu cầu hàng tháng
Bước 3: Xác định miền nghiệm.
b) Lợi nhuận hàng tháng bằng lợi nhuận bán x máy loại A và y máy loại B.
c)
Bước 1: Xác định giá trị của F tại các điểm thuộc miền đa giác biểu diễn miền nghiệm của hệ bất phương trình ở câu a.
Bước 2: Giá trị lớn nhất của F là số lớn nhất trong các số tìm được ở bước 1.
Lời giải chi tiết:
a)
Bước 1: Ta có:
Loại A | Loại B | |
Giá mua vào | 10 triệu đồng/1 máy | 20 triệu đồng/1 máy |
Lợi nhuận | 2,5 triệu đồng/1 máy | 4 triệu đồng/1 máy |
Bước 2: Lập hệ bất phương trình
Vì số lượng máy là số tự nhiên nên ta có \(x \ge 0;y \ge 0\)
Vốn nhập vào x máy loại A và y máy loại B là \(10x + 20y\)(triệu đồng)
4 tỉ đồng=4000 (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có bất phương trình
\(10x + 20y \le 4000\) \( \Leftrightarrow x + 2y \le 400\)
Vì tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy nên ta có \(x + y \le 250\).
Vậy ta có hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Bước 3: Xác định miền nghiệm
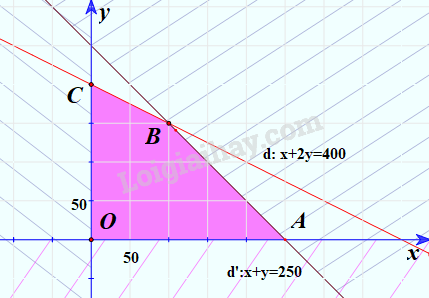
Miền nghiệm là tứ giác OABC với tọa độ các đỉnh này là O(0;0), A(250;0), B(100;150), C(0;200)
b) Lợi nhuận hàng tháng là F(x;y)=2,5x+4y(triệu đồng)
c) Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Ta có F(0;0)=0, F(250;0)=2,5.250+4.0=625
F(100;150)=2,5.100+4.150=850
F(0;200)=2,5.0+4.200=800
Giá trị lớn nhất là F(100;150)=850.
Vậy cửa hàng cần đầu tư kinh doanh 100 máy A và 150 máy B.
Xét biểu thức F(x, y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Toạ độ ba đình là O(0, 0), A(150, 0) và B(0; 150) (H.2.5).
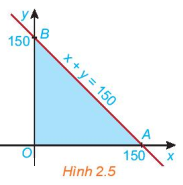
a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.
b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.
c) Nêu nhận xét về tổng x + y của điểm (X; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x, y) trên miền tam giác OAB.
Phương pháp giải:
a) Thay tọa độ điểm O, A, B vào F(x;y) và tính giá trị.
b) Lấy một điểm bất kì trong miền tam giác OAB.
Xác định dấu:
+ So sánh x với 0
+ So sánh y với 0
Đánh giá biểu thức F(x;y) dựa vào dấu của x và y, từ đó tìm giá trị nhỏ nhất của biểu thức.
c)
Dựa vào biểu thức
Giá trị lớn nhất: Tách 2x+3y =2.(x+y)+y và dựa vào việc đánh giá x+y và y ở bước trên để tìm giá trị lớn nhất.
Lời giải chi tiết:
a) Thay tọa độ điểm O, A, B vào F(x;y) ta được:
F(0;0)=2.0+3.0=0
F(150;0)=2.150+3.0=300
F(0;150)=2.0+3.150=450.
b) Lấy một điểm bất kì trong miền tam giác OAB.
Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x \ge 0\).
Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(y \ge 0\).
Vậy \(x \ge 0\) và \(y \ge 0\).
=> \(F\left( {x;y} \right) = 2x + 3y \ge 2.0 + 3.0 = 0\)
Vậy giá trị nhỏ nhất của F(x;y) trên miền OAB là 0.
c) Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x + y \le 150\)
Như vậy với mỗi điểm trong miền tam giác OAB thì đều có tổng \(x + y \le 150\)
Quan sát miền OAB ta thấy điểm B(0;150) là điểm có tung độ lớn nhất nên mọi điểm (x;y) thuộc miền OAB đều có \(y \le 150\).
Vậy ta có: \(F\left( {x;y} \right) = 2x + 3y\)\( = 2.\left( {x + y} \right) + y\)\( \le 2.150 + 150 = 450\)
Dấu “=” xảy ra khi x+y=150 và y=150. Hay x=0, y=150.
Giá trị lớn nhất trên miền OAB là 450 tại điểm B.
Xét biểu thức F(x, y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Toạ độ ba đình là O(0, 0), A(150, 0) và B(0; 150) (H.2.5).
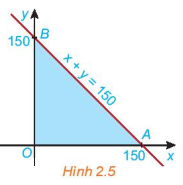
a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.
b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.
c) Nêu nhận xét về tổng x + y của điểm (X; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x, y) trên miền tam giác OAB.
Phương pháp giải:
a) Thay tọa độ điểm O, A, B vào F(x;y) và tính giá trị.
b) Lấy một điểm bất kì trong miền tam giác OAB.
Xác định dấu:
+ So sánh x với 0
+ So sánh y với 0
Đánh giá biểu thức F(x;y) dựa vào dấu của x và y, từ đó tìm giá trị nhỏ nhất của biểu thức.
c)
Dựa vào biểu thức
Giá trị lớn nhất: Tách 2x+3y =2.(x+y)+y và dựa vào việc đánh giá x+y và y ở bước trên để tìm giá trị lớn nhất.
Lời giải chi tiết:
a) Thay tọa độ điểm O, A, B vào F(x;y) ta được:
F(0;0)=2.0+3.0=0
F(150;0)=2.150+3.0=300
F(0;150)=2.0+3.150=450.
b) Lấy một điểm bất kì trong miền tam giác OAB.
Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x \ge 0\).
Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(y \ge 0\).
Vậy \(x \ge 0\) và \(y \ge 0\).
=> \(F\left( {x;y} \right) = 2x + 3y \ge 2.0 + 3.0 = 0\)
Vậy giá trị nhỏ nhất của F(x;y) trên miền OAB là 0.
c) Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x + y \le 150\)
Như vậy với mỗi điểm trong miền tam giác OAB thì đều có tổng \(x + y \le 150\)
Quan sát miền OAB ta thấy điểm B(0;150) là điểm có tung độ lớn nhất nên mọi điểm (x;y) thuộc miền OAB đều có \(y \le 150\).
Vậy ta có: \(F\left( {x;y} \right) = 2x + 3y\)\( = 2.\left( {x + y} \right) + y\)\( \le 2.150 + 150 = 450\)
Dấu “=” xảy ra khi x+y=150 và y=150. Hay x=0, y=150.
Giá trị lớn nhất trên miền OAB là 450 tại điểm B.
Một cửa hàng có kế hoạch nhập về hai loại máy tính A và B, giá mỗi chiếc lần lượt là 10 triệu đồng và 20 triệu đồng với số vốn ban đầu không vượt quá 4 tỉ đồng. Loại máy A mang lại lợi nhuận 2,5 triệu đồng cho mỗi máy bán được và loại máy B mang lại lợi nhuận là 4 triệu đồng mỗi máy. Cửa hàng ước tính rằng tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy. Giả sử trong một tháng cửa hàng cần nhập số máy tính loại A là x và số máy tính loại B là y.
a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương
trình rồi xác định miền nghiệm của hệ đó.
b) Gọi F (triệu đồng) là lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B. Hãy biểu diễn F theo x và y.
c) Tìm số lượng máy tính mỗi loại cửa hàng cần nhập về trong tháng đó đề lợi nhuận thu được là lớn nhất.
Phương pháp giải:
a)
Bước 1: Lập bảng thể hiện vốn và lợi nhuận của mỗi loại máy.
Bước 2: Dựa vào các điều kiện sau để lập bất phương trình:
+ Số lượng là số tự nhiên
+ Điều kiện vốn ban đầu
+ Nhu cầu hàng tháng
Bước 3: Xác định miền nghiệm.
b) Lợi nhuận hàng tháng bằng lợi nhuận bán x máy loại A và y máy loại B.
c)
Bước 1: Xác định giá trị của F tại các điểm thuộc miền đa giác biểu diễn miền nghiệm của hệ bất phương trình ở câu a.
Bước 2: Giá trị lớn nhất của F là số lớn nhất trong các số tìm được ở bước 1.
Lời giải chi tiết:
a)
Bước 1: Ta có:
Loại A | Loại B | |
Giá mua vào | 10 triệu đồng/1 máy | 20 triệu đồng/1 máy |
Lợi nhuận | 2,5 triệu đồng/1 máy | 4 triệu đồng/1 máy |
Bước 2: Lập hệ bất phương trình
Vì số lượng máy là số tự nhiên nên ta có \(x \ge 0;y \ge 0\)
Vốn nhập vào x máy loại A và y máy loại B là \(10x + 20y\)(triệu đồng)
4 tỉ đồng=4000 (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có bất phương trình
\(10x + 20y \le 4000\) \( \Leftrightarrow x + 2y \le 400\)
Vì tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy nên ta có \(x + y \le 250\).
Vậy ta có hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Bước 3: Xác định miền nghiệm
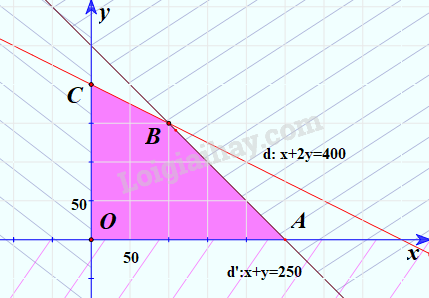
Miền nghiệm là tứ giác OABC với tọa độ các đỉnh này là O(0;0), A(250;0), B(100;150), C(0;200)
b) Lợi nhuận hàng tháng là F(x;y)=2,5x+4y(triệu đồng)
c) Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Ta có F(0;0)=0, F(250;0)=2,5.250+4.0=625
F(100;150)=2,5.100+4.150=850
F(0;200)=2,5.0+4.200=800
Giá trị lớn nhất là F(100;150)=850.
Vậy cửa hàng cần đầu tư kinh doanh 100 máy A và 150 máy B.
Mục 3 trong SGK Toán 10 tập 1 - Kết nối tri thức tập trung vào các kiến thức về vectơ, bao gồm các khái niệm cơ bản, các phép toán trên vectơ, và ứng dụng của vectơ trong hình học. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán.
Bài tập này yêu cầu học sinh hiểu rõ khái niệm vectơ, các yếu tố của vectơ, và cách biểu diễn vectơ trên mặt phẳng tọa độ. Các em cần phân biệt được vectơ với đoạn thẳng, và biết cách xác định độ dài của vectơ.
Bài tập này tập trung vào các phép cộng, trừ, nhân với một số thực của vectơ. Học sinh cần nắm vững các quy tắc thực hiện các phép toán này, và biết cách áp dụng chúng để giải các bài toán cụ thể.
Bài tập này yêu cầu học sinh sử dụng kiến thức về vectơ để giải các bài toán liên quan đến hình học, chẳng hạn như chứng minh hai đường thẳng song song, tìm giao điểm của hai đường thẳng, hoặc tính diện tích của một hình.
| Bài tập | Nội dung |
|---|---|
| 3.1 | Chứng minh hai đường thẳng song song bằng vectơ. |
| 3.2 | Tìm giao điểm của hai đường thẳng bằng phương pháp vectơ. |
| 3.3 | Tính diện tích tam giác bằng vectơ. |
| Lưu ý: Cần vẽ hình minh họa để dễ dàng hình dung và giải quyết bài toán. | |
Giaitoan.edu.vn cung cấp lời giải chi tiết cho từng bài tập trong mục 3 trang 28, 29, 30 SGK Toán 10 tập 1 - Kết nối tri thức. Các lời giải được trình bày rõ ràng, dễ hiểu, kèm theo các bước giải cụ thể và các lưu ý quan trọng. Bên cạnh đó, chúng tôi cũng cung cấp các bài tập tương tự để các em có thể luyện tập và củng cố kiến thức.
Để học tốt môn Toán, các em cần:
Hy vọng rằng với những lời giải chi tiết và hướng dẫn cụ thể mà giaitoan.edu.vn cung cấp, các em sẽ học tốt môn Toán 10 và đạt được kết quả cao trong các kỳ thi. Chúc các em thành công!