Bài 8 trang 96 SGK Toán 10 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học phẳng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 96 SGK Toán 10 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
a) Biểu diễn miền nghiệm D của bất phương trình bậc nhất hai ẩn sau:
Đề bài
a) Biểu diễn miền nghiệm D của bất phương trình bậc nhất hai ẩn sau:
\(\left\{ \begin{array}{l}x - y \le 6\\2x - y \le 2\\x \ge 0\\y \ge 0\end{array} \right.\)
b) Từ kết quả câu a, tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F(x;y) = 2x + 3y\) trên miền D.
Lời giải chi tiết
+ Biểu diễn miền nghiệm của BPT \(x - y \le 6\)
Bước 1: Vẽ đường thẳng \(d:x - y = 6\) trên mặt phẳng tọa độ Õy
Bước 2: Lấy O(0;0) không thuộc d, ta có: \(0 - 0 = 0 \le 6\) => điểm O(0;0) thuộc miền nghiệm
=> Miền nghiệm của BPT \(x - y \le 6\) là nửa mp bờ d, chứa gốc tọa độ.
+ Tương tự, ta có miền nghiệm của BPT \(2x - y \le 2\) là nửa mp bờ \(d':2x - y = 0\), chứa gốc tọa độ.
+ Miền nghiệm của BPT \(x \ge 0\) là nửa mp bên phải Oy (tính cả trục Oy)
+ Miền nghiệm của BPT \(y \ge 0\) là nửa mp phía trên Ox (tính cả trục Ox)
Biểu diễn trên cùng một mặt phẳng tọa độ và gạch bỏ các miền không là nghiệm của từng BPT, ta được:
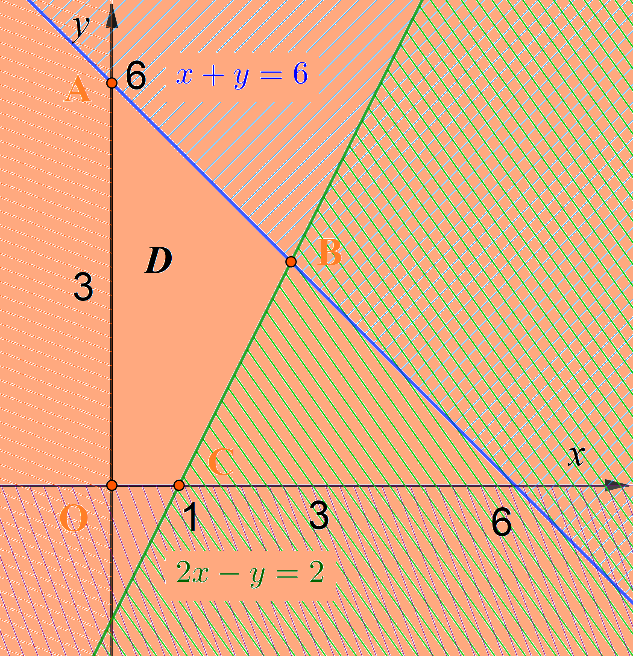
Miền nghiệm của hệ bất phương trình đã cho là miền tứ giác OABC (miền không bị gạch) với \(A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\)
b)
Thay tọa độ các điểm \(O(0;0),A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\) và biểu thức \(F(x;y) = 2x + 3y\) ta được:
\(\begin{array}{l}F(0;0) = 2.0 + 3.0 = 0\\F(0;6) = 2.0 + 3.6 = 18\\F(\frac{8}{3};\frac{{10}}{3}) = 2.\frac{8}{3} + 3.\frac{{10}}{3} = \frac{{46}}{3}\\F(1;0) = 2.1 + 3.0 = 2\end{array}\)
\( \Rightarrow \min F = 0\), \(\max F = 18\)
Vậy trên miền D, giá trị nhỏ nhất của F bằng 0, giá trị lớn nhất của F bằng \(18\).
Bài 8 trang 96 SGK Toán 10 – Kết nối tri thức thuộc chương 1: Vectơ trong mặt phẳng. Bài tập này tập trung vào việc vận dụng các kiến thức về phép cộng, trừ vectơ, tích của một số với vectơ, và các tính chất của chúng để giải quyết các bài toán liên quan đến hình học phẳng. Việc nắm vững các khái niệm và định lý liên quan là yếu tố then chốt để giải quyết bài toán này một cách hiệu quả.
Bài 8 bao gồm các câu hỏi và bài tập yêu cầu học sinh:
Đề bài: Cho hình bình hành ABCD. Gọi M là trung điểm của BC. Chứng minh rằng: AM và CD cùng phương.
Lời giải:
Đề bài: Gọi N là trung điểm của AD. Chứng minh rằng: AN và MC cùng phương.
Lời giải:
Bài tập này là một ví dụ điển hình về việc sử dụng vectơ để chứng minh các tính chất hình học. Các kiến thức về vectơ có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như vật lý, kỹ thuật, và khoa học máy tính. Việc nắm vững các khái niệm và kỹ năng liên quan đến vectơ sẽ giúp học sinh giải quyết các bài toán phức tạp hơn trong tương lai.
Bài 8 trang 96 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập này và các bài tập tương tự.