Bài 6.14 trang 16 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết vấn đề.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.14 trang 16 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Quỹ đạo của vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa độ Oxy là một parabol có phương trình
Đề bài
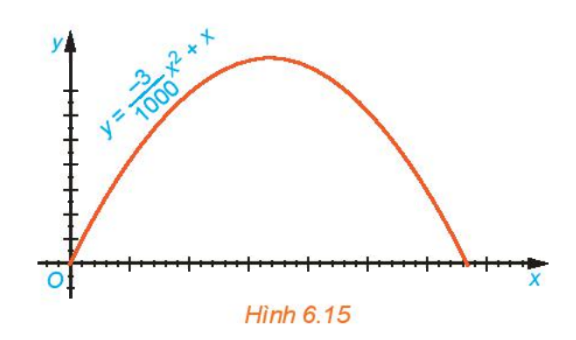
Quỹ đạo của vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa độ Oxy là một parabol có phương trình \(y = \frac{{ - 3}}{{1000}}{x^2} + x\) , trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất (H.6.15)
a) Tím độ cao cực đại của vật trong quá trình bay
b) Tính khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O. Khoảng cách này gọi là tầm xa của quỹ đạo.
Phương pháp giải - Xem chi tiết
a) Độ cao cực đại của vật là tung độ đỉnh của hàm số \(y = \frac{{ - 3}}{{1000}}{x^2} + x\)
b) Khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O là hoành độ của điểm khác gốc tọa độ làm cho y=0
Lời giải chi tiết
a) Tung độ đỉnh của hàm số \(y = \frac{{ - 3}}{{1000}}{x^2} + x\) là:
\(\frac{{ - \Delta }}{{4a}} = \frac{{ - \left( {{1^2} - 4.\frac{{ - 3}}{{1000}}.0} \right)}}{{4.\frac{{ - 3}}{{1000}}}} = \frac{{250}}{3}\)
Vậy độ cao cực đại của vật là \(\frac{{250}}{3}(m)\)
b) Vật chạm đất khi:
\(y = 0 \Leftrightarrow \frac{{ - 3}}{{1000}}{x^2} + x = 0 \Leftrightarrow x = \frac{{1000}}{3}\)và x=0(loại)
Vậy khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O là \(\frac{{1000}}{3}\left( m \right)\)
Bài 6.14 trang 16 SGK Toán 10 – Kết nối tri thức thuộc chương 1: Vectơ trong mặt phẳng. Bài tập này tập trung vào việc vận dụng các kiến thức đã học về vectơ, đặc biệt là các phép toán cộng, trừ vectơ và phép nhân vectơ với một số thực để giải quyết các bài toán liên quan đến hình học.
Bài tập yêu cầu học sinh chứng minh một đẳng thức vectơ liên quan đến các điểm và vectơ trong một hình bình hành. Để giải bài tập này, học sinh cần nắm vững các quy tắc cộng, trừ vectơ và hiểu rõ mối quan hệ giữa các vectơ trong hình bình hành.
Đề bài: Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Gọi N là giao điểm của AM và BD. Chứng minh rằng: BN = 2ND.
Lời giải:
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự sau:
Bài 6.14 trang 16 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài tập vectơ. Hy vọng với lời giải chi tiết và các kiến thức liên quan được cung cấp, các em học sinh sẽ hiểu rõ hơn về bài tập này và tự tin giải các bài tập tương tự.