Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 4, trang 54, 55 và 56 của sách giáo khoa Toán 10 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
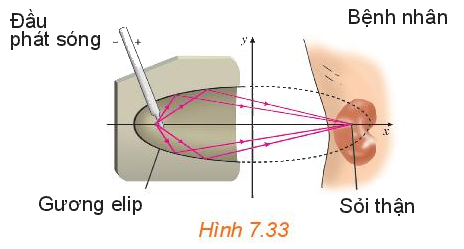
Gương elip trong một máy tán sỏi thận (H7.33) ứng với clip có phương trình chính tắc
Đề bài
Vận dụng 3 trang 56 SGK Toán 10 - Kết nối tri thức
Gương elip trong một máy tán sỏi thận (H7.33) ứng với clip có phươngtrình chính tắc là \(\frac{{{x^2}}}{{400}} + \frac{{{y^2}}}{{76}} = 1\) (theo đơn vị cm). Tính khoảng cách từ vị trí đầu phát sóng của máy đến vị trí của sỏi thận cần tán.
Lời giải chi tiết
Vị tri bắt đầu phát sóng của máy và vị trí viên sỏi được đặt ở hai tiêu điểm của gương elip, do đó khoảng cách cần tìm là tiêu cự của gương và bằng \(2c = 2\sqrt {400 - 76} = 36\left( {cm} \right)\).
Mục 4 của chương trình Toán 10 tập 2 - Kết nối tri thức tập trung vào việc nghiên cứu về vectơ và các ứng dụng của vectơ trong hình học. Nội dung chính bao gồm định nghĩa vectơ, các phép toán trên vectơ (cộng, trừ, nhân với một số thực), và các tính chất của các phép toán này. Ngoài ra, mục này còn giới thiệu về tích vô hướng của hai vectơ và ứng dụng của tích vô hướng trong việc xác định góc giữa hai vectơ, tính độ dài của vectơ, và chứng minh các tính chất hình học.
Các bài tập trên trang 54 chủ yếu tập trung vào việc kiểm tra sự hiểu biết của học sinh về định nghĩa vectơ, cách biểu diễn vectơ, và cách thực hiện các phép toán cộng, trừ vectơ. Các bài tập thường yêu cầu học sinh xác định vectơ, tìm tọa độ của vectơ, và tính toán các phép toán trên vectơ dựa trên tọa độ của chúng.
Trang 55 tiếp tục củng cố kiến thức về các phép toán trên vectơ, nhưng tập trung hơn vào việc áp dụng các tính chất của các phép toán này để đơn giản hóa các biểu thức và giải các bài toán. Các bài tập thường yêu cầu học sinh sử dụng các tính chất giao hoán, kết hợp, phân phối của phép cộng và phép nhân vectơ để biến đổi các biểu thức vectơ.
Trang 56 giới thiệu về tích vô hướng của hai vectơ và các ứng dụng của nó. Các bài tập trên trang này yêu cầu học sinh tính tích vô hướng của hai vectơ, sử dụng tích vô hướng để tính góc giữa hai vectơ, và áp dụng tích vô hướng để chứng minh các tính chất hình học.
| Bài tập | Nội dung |
|---|---|
| Bài 7 | Tính tích vô hướng của hai vectơ cho trước. |
| Bài 8 | Tìm góc giữa hai vectơ. |
| Bài 9 | Chứng minh hai vectơ vuông góc. |
Để giải tốt các bài tập trong mục 4, các em cần nắm vững định nghĩa vectơ, các phép toán trên vectơ, và các tính chất của các phép toán này. Ngoài ra, các em cũng cần hiểu rõ về tích vô hướng của hai vectơ và các ứng dụng của nó. Khi giải bài tập, các em nên vẽ hình để minh họa các vectơ và các phép toán trên chúng. Điều này sẽ giúp các em hiểu rõ hơn về bài toán và tìm ra lời giải chính xác.
Hy vọng rằng với lời giải chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 4 trang 54, 55, 56 SGK Toán 10 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!