Hệ bất phương trình bậc nhất hai ẩn là một trong những kiến thức quan trọng trong chương trình toán học lớp 10. Việc nắm vững lý thuyết và phương pháp giải hệ bất phương trình này sẽ giúp bạn giải quyết nhiều bài toán thực tế và là nền tảng cho các kiến thức toán học nâng cao.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về lý thuyết Hệ bất phương trình bậc nhất hai ẩn, kèm theo các ví dụ minh họa và bài tập thực hành để bạn có thể tự tin làm chủ kiến thức này.
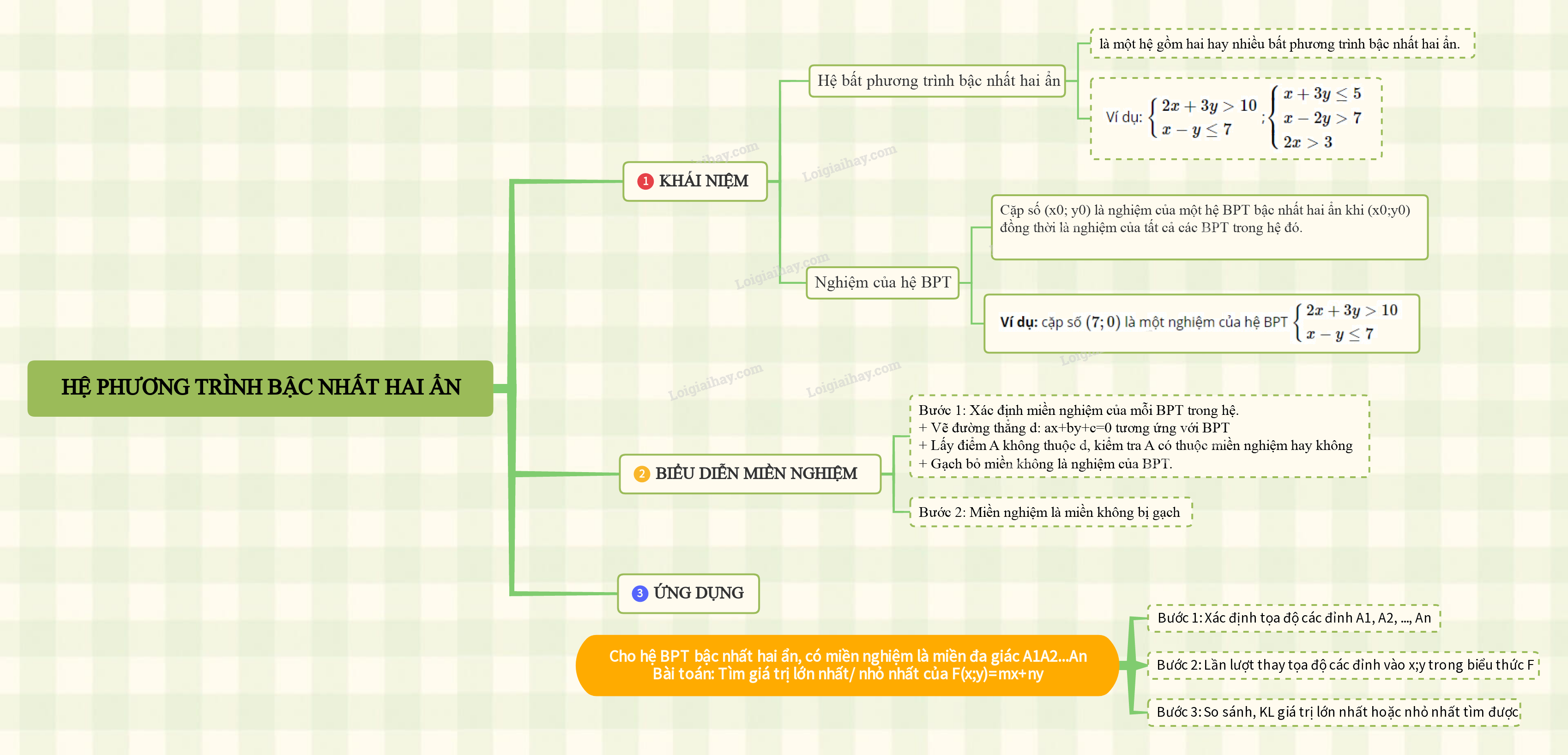
1. Hệ bất phương trình bậc nhất hai ẩn
1. Hệ bất phương trình bậc nhất hai ẩn
+) Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.
Ví dụ: \(\left\{ \begin{array}{l}2x + 3y > 10\\x - y \le 7\end{array} \right.\);\(\left\{ \begin{array}{l}x + 3y \le 5\\x - 2y > 7\\2x > 3\end{array} \right.\)
+) Cặp số \(({x_0};{y_0})\) là nghiệm của một hệ BPT bậc nhất hai ẩn khi \(({x_0};{y_0})\) đồng thời là nghiệm của tất cả các BPT trong hệ đó.
Ví dụ: cặp số \((7;0)\) là một nghiệm của hệ BPT \(\left\{ \begin{array}{l}2x + 3y > 10\\x - y \le 7\end{array} \right.\)
2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ
+) Miền nghiệm là tập hợp các điểm có tọa độ (x;y) là nghiệm của hệ bất phương trình bậc nhất hai ẩn đó.
+) Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.
+) Cách xác định miền nghiệm của một hệ BPT bậc nhất hai ẩn:
Bước 1: Xác định miền nghiệm của mỗi BPT trong hệ và gạch bỏ miền còn lại.
Bước 2: Miền không bị gạch là miền nghiệm của hệ BPT đã cho.
3. Ứng dụng của hệ bất phương trình bậc nhất hai ẩn
Cho hệ BPT bậc nhất hai ẩn x, y có miền nghiệm là miền đa giác \({A_1}{A_2}...{A_n}\).
Tìm gía trị lớn nhất, nhỏ nhất của biểu thức \(F(x;y) = mx + ny\)
Bước 1: Tính giá trị của F tương ứng với (x;y) là tọa độ các đỉnh
Bước 2: Kết luận
Giá trị lớn nhất của F là số lớn nhất trong các giá trị thu được.
Giá trị nhỏ nhất của F là số bé nhất trong các giá trị thu được.
Hệ bất phương trình bậc nhất hai ẩn là một tập hợp các bất phương trình bậc nhất hai ẩn được liên kết với nhau. Để hiểu rõ hơn về hệ bất phương trình này, chúng ta cần nắm vững các khái niệm cơ bản sau:
Bất phương trình bậc nhất hai ẩn có dạng tổng quát: ax + by < c (hoặc ax + by ≤ c, ax + by > c, ax + by ≥ c), trong đó a, b, và c là các số thực, và x, y là các ẩn số.
Ví dụ: 2x + y ≤ 5, -x + 3y > 1
Miền nghiệm của bất phương trình bậc nhất hai ẩn là tập hợp tất cả các điểm (x, y) thỏa mãn bất phương trình đó. Để biểu diễn miền nghiệm trên mặt phẳng tọa độ, ta thực hiện các bước sau:
Hệ bất phương trình bậc nhất hai ẩn là tập hợp các bất phương trình bậc nhất hai ẩn được xét đồng thời. Ví dụ:
{ 2x + y ≤ 5x - y > 1 }
Miền nghiệm của hệ bất phương trình bậc nhất hai ẩn là giao của các miền nghiệm của từng bất phương trình trong hệ. Để tìm miền nghiệm của hệ, ta thực hiện các bước sau:
Xét hệ bất phương trình sau:
{ x + y ≤ 2x - y ≥ 0x ≥ 0y ≥ 0 }
Vẽ các đường thẳng tương ứng và xác định miền nghiệm của từng bất phương trình. Giao của các miền nghiệm này là một tứ giác. Miền nghiệm của hệ là tứ giác đó.
Hy vọng với những kiến thức trên, bạn đã có cái nhìn tổng quan về lý thuyết Hệ bất phương trình bậc nhất hai ẩn. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập.