Bài 4.10 trang 54 SGK Toán 10 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.10 trang 54 SGK Toán 10 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng không khổi và có độ lớn bàng nhau. Hai tàu luôn dược giữ lái sao cho chúng tạo với bờ cùng một góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận tốc dòng nước là đáng kể, các yêu tố bên ngoài khác không ảnh hưởng tới vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước.
Đề bài
Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng không đổi và có độ lớn bằng nhau. Hai tàu luôn được giữ lái sao cho chúng tạo với bờ cùng một góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận tốc dòng nước là đáng kể, các yêu tố bên ngoài khác không ảnh hưởng tới vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước.
Phương pháp giải - Xem chi tiết
Biểu diễn hướng đi của hai tàu.
Phân tích theo vectơ vận tốc riêng và vận tốc dòng nước.
Lời giải chi tiết
Coi hai bờ sông lần lượt là đường thẳng \({d_1},{d_2}.\) Giả sử tàu 1 xuất phát từ A hướng về hạ lưu và tàu 2 xuất phát từ B hướng về thượng nguồn như hình vẽ.
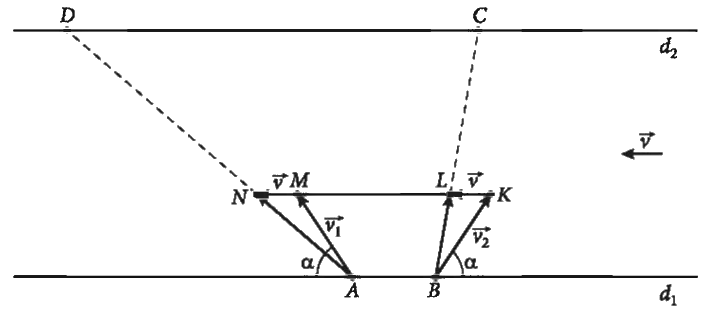
Ta sử dụng các vecto \(\overrightarrow v ,\overrightarrow {{v_1}} ,\overrightarrow {{v_2}} \) để biểu diễn cho vận tốc của dòng nước, vận tốc riêng của tàu 1 và tàu 2.
Lấy các điểm K, M sao cho \(\overrightarrow {BK} = \overrightarrow {{v_2}} ,\overrightarrow {AM} = \overrightarrow {{v_1}} .\) Từ giả thiết suy ra tứ giác ABKM là một hình thang cân.
Lấy các điểm L, N sao cho \(\overrightarrow {KL} = \overrightarrow v = \overrightarrow {MN} \). Khi đó K, L, M, N cùng nằm trên một đường thẳng song song với \({d_1},{d_2}\) và các vecto \(\overrightarrow {AN} = \overrightarrow {{v_1}} + \overrightarrow v ,\overrightarrow {BL} = \overrightarrow {{v_2}} + \overrightarrow v \) tương ứng biểu diễn cho vận tốc thực của tàu 1 và tàu 2.
Khi đó tàu 1 chuyển động theo hướng \(\overrightarrow {AN} \) đến đích là điểm D. Tàu 2 theo hướng \(\overrightarrow {BL} \) đến đích là điểm C.
Do các đường thẳng KL, MN, \({d_1},{d_2}\) đôi một song song nên theo định lí Ta-lét ta có: \(\frac{{AD}}{{AN}} = \frac{{BC}}{{BL}} = k\).
Trong đó AD, AN là quãng đường đi và độ lớn vận tốc của tàu 1 còn BC, BL là quãng đường đi và độ lớn vận tốc của tàu 2.
Như vậy hai tàu cần thời gian như nhau để sang bờ bên kia.
Vậy hai tàu sang đến bờ bên kia cùng một lúc.
Bài 4.10 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức là một bài toán ứng dụng kiến thức về vectơ trong hình học. Để giải bài toán này, học sinh cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ và cách sử dụng vectơ để biểu diễn các yếu tố hình học.
Cho hình vuông ABCD có cạnh bằng a. Gọi M là trung điểm của cạnh BC. Tính độ dài của vectơ AM.
Để giải bài toán này, ta có thể sử dụng phương pháp tọa độ hoặc phương pháp vectơ hình học. Dưới đây là lời giải bằng phương pháp vectơ hình học:
AM = M - A = (a; a/2) - (0; 0) = (a; a/2)
|AM| = √((a)^2 + (a/2)^2) = √(a^2 + a^2/4) = √(5a^2/4) = (a√5)/2
Vậy độ dài của vectơ AM là (a√5)/2.
Bài toán này giúp học sinh hiểu rõ hơn về cách sử dụng vectơ để tính độ dài đoạn thẳng trong hình học. Ngoài ra, bài toán còn có thể được mở rộng bằng cách thay đổi vị trí của điểm M hoặc thay đổi hình dạng của hình ABCD.
Để rèn luyện thêm kỹ năng giải bài tập về vectơ, học sinh có thể tham khảo các bài tập tương tự sau:
Bài 4.10 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng trong hình học. Hy vọng với lời giải chi tiết và phân tích trên, các em học sinh sẽ hiểu rõ hơn về bài toán và tự tin giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để tìm kiếm thêm nhiều tài liệu học tập hữu ích khác.