Chào mừng bạn đến với bài học về Lý thuyết Tổng và hiệu của hai vecto, một phần quan trọng trong chương trình SGK Toán 10 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và cần thiết để hiểu rõ về phép cộng, phép trừ vecto và ứng dụng của chúng trong giải quyết các bài toán hình học.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và đầy đủ, giúp bạn tự tin chinh phục môn Toán.
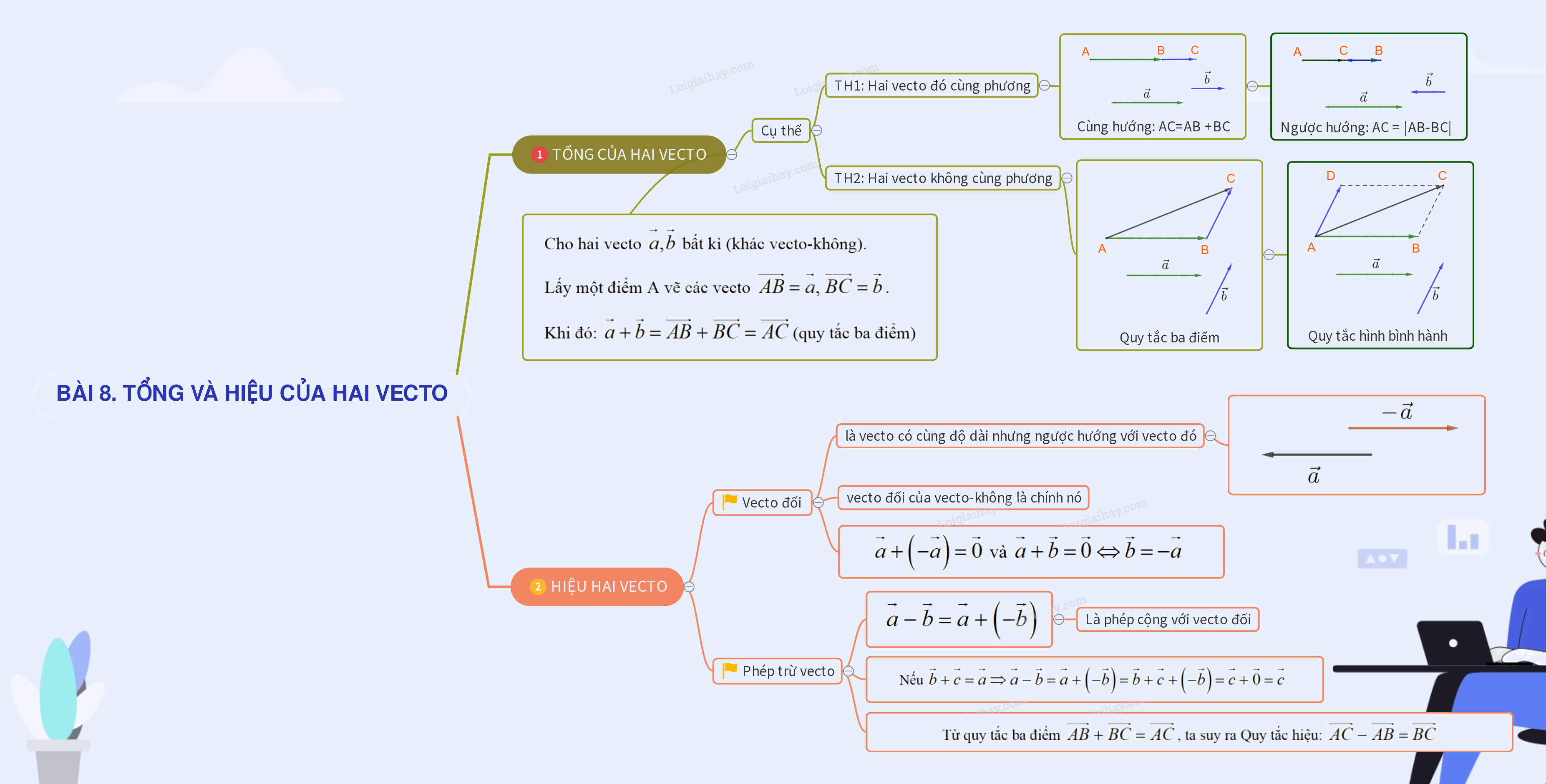
1. TỔNG CỦA HAI VECTƠ 2. HIỆU CỦA HAI VECTƠ
1. TỔNG CỦA HAI VECTƠ
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) bất kì (khác vecto-không). Lấy một điểm A vẽ các vecto \(\overrightarrow {AB} = \overrightarrow a ,\;\overrightarrow {BC} = \overrightarrow b \).
Khi đó: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)(quy tắc ba điểm)
a) Tổng hai vecto cùng phương \(\overrightarrow a ,\overrightarrow b \)
+) TH1: hai vecto \(\overrightarrow a ,\overrightarrow b \) cùng hướng: AC = AB + BC
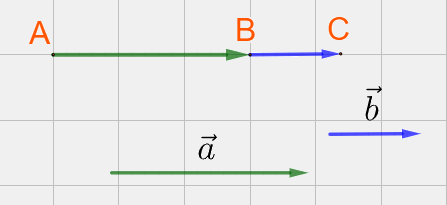
+) TH2: hai vecto \(\overrightarrow a ,\overrightarrow b \) ngược hướng: AC = |AB – BC|
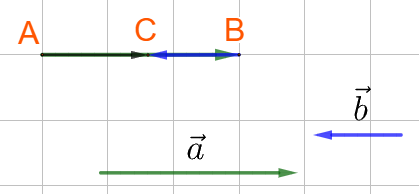
b) Tổng hai vecto không cùng phương
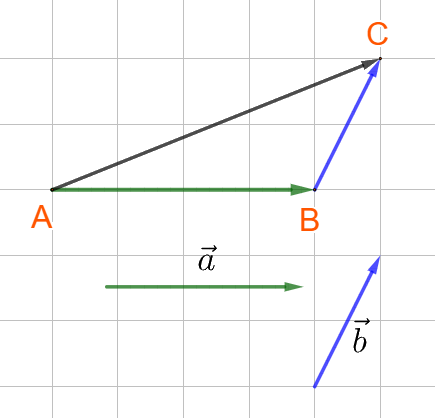
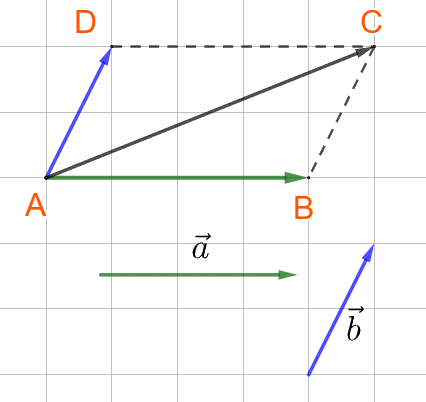
Nhận xét: vecto \(\overrightarrow {AC} \) là đường chéo của hình bình hành ABCD.
Do \(\overrightarrow {BC} = \overrightarrow {AD} \). Ta viết: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)(quy tắc hình bình hành)
2. HIỆU CỦA HAI VECTƠ
+) Vecto đối của vecto \(\overrightarrow a \): là vecto có cùng độ dài nhưng ngược hướng với vecto\(\overrightarrow a \).
Kí hiệu: \( - \;\overrightarrow a \)
Đặc biệt: Vecto đối của vecto \(\overrightarrow 0 \) là chính nó.
Chú ý: \(\overrightarrow a + \left( { - \overrightarrow a } \right) = \overrightarrow 0 \) và \(\overrightarrow a + \overrightarrow b = \overrightarrow 0 \Leftrightarrow \overrightarrow b = - \overrightarrow a \)
+) Phép trừ vecto: \(\overrightarrow a - \overrightarrow b = \overrightarrow a + \left( { - \overrightarrow b } \right)\)
Chú ý: Nếu \(\overrightarrow b + \overrightarrow c = \overrightarrow a \Rightarrow \overrightarrow a - \overrightarrow b = \overrightarrow c \)
Từ quy tắc ba điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \), ta suy ra:
\( \Rightarrow \overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {BC} \) (quy tắc hiệu)
Từ quy tắc ba điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \), ta suy ra Quy tắc hiệu: \(\overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {BC} \)
Trong chương trình Toán 10, phần vectơ đóng vai trò quan trọng trong việc xây dựng nền tảng cho các kiến thức hình học và vật lý ở các lớp trên. Một trong những nội dung cơ bản và thiết yếu của phần này là lý thuyết về tổng và hiệu của hai vectơ. Bài viết này sẽ trình bày chi tiết lý thuyết này, kèm theo các ví dụ minh họa và bài tập để giúp bạn hiểu rõ hơn.
Trước khi đi vào lý thuyết về tổng và hiệu của hai vectơ, chúng ta cần nhắc lại định nghĩa về vectơ. Một vectơ được xác định bởi hướng và độ dài. Vectơ thường được biểu diễn bằng một đoạn thẳng có mũi tên chỉ hướng. Ký hiệu vectơ thường là một chữ cái in hoa hoặc một cặp điểm (ví dụ: AB).
Phép cộng vectơ là một phép toán cơ bản trong hình học vectơ. Để cộng hai vectơ a và b, ta sử dụng quy tắc hình bình hành hoặc quy tắc tam giác.
Tính chất của phép cộng vectơ:
Phép trừ vectơ là phép toán ngược của phép cộng vectơ. Để trừ vectơ b khỏi vectơ a, ta cộng vectơ a với vectơ đối của vectơ b, ký hiệu là -b.
Vectơ đối của một vectơ có cùng độ dài và cùng phương nhưng ngược chiều với vectơ ban đầu.
a - b = a + (-b)
Ví dụ 1: Cho hai vectơ a và b có độ dài lần lượt là 3 và 4, và góc giữa chúng là 60 độ. Tính độ dài của vectơ a + b.
Áp dụng công thức tính độ dài của vectơ tổng:
|a + b|2 = |a|2 + |b|2 + 2|a||b|cos(60°)
|a + b|2 = 32 + 42 + 2 * 3 * 4 * 0.5 = 9 + 16 + 12 = 37
|a + b| = √37
Ví dụ 2: Cho tam giác ABC, M là trung điểm của BC. Chứng minh rằng MA + MB + MC = 0.
Vì M là trung điểm của BC, ta có MB = MC. Do đó, MA + MB + MC = MA + 2MC. Sử dụng quy tắc hình bình hành, ta có MA + MC = BA. Vậy MA + MB + MC = BA + MB = 0.
Bài 1: Cho hai vectơ a và b vuông góc với nhau và có độ dài lần lượt là 5 và 12. Tính độ dài của vectơ a - b.
Bài 2: Cho hình vuông ABCD có cạnh bằng a. Tính độ dài của vectơ AB + AD.
Bài 3: Cho tam giác ABC. Gọi G là trọng tâm của tam giác. Chứng minh rằng GA + GB + GC = 0.
Lý thuyết về tổng và hiệu của hai vectơ là một phần quan trọng trong chương trình Toán 10. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết và hữu ích về chủ đề này.