Bài 3.16 trang 44 SGK Toán 10 tập 1 thuộc chương 3: Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.16, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Hãy cùng theo dõi lời giải chi tiết dưới đây!
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
Đề bài
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
a) \(\cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
b) \(M{A^2} + M{B^2} - A{B^2} = 2.MA.MB.\cos \widehat {AMB}\) và \(M{A^2} + M{C^2} - A{C^2} = 2.MA.MC.\cos \widehat {AMC}\)
c) \(M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\) (công thức đường trung tuyến).
Phương pháp giải - Xem chi tiết
a) Giá trị lượng giác của hai góc bù nhau:
\( - \cos x = \cos \left( {{{180}^o} - x} \right)\)
b) Định lí cos: \({a^2} = {b^2} + {c^2} - 2bc\;\cos A\)cho tam giác tương ứng.
c) Suy ra từ b, lưu ý rằng: \(\left\{ \begin{array}{l}\cos \widehat {AMC} + \cos \widehat {AMB} = 0\\MB = MC = \frac{{BC}}{2}\end{array} \right.\)
Lời giải chi tiết
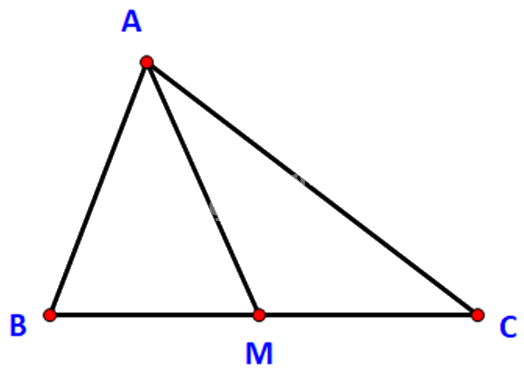
a) Ta có: \(\widehat {AMB} + \widehat {AMC} = {180^o}\)
\( \Rightarrow \cos \widehat {AMB} = - \cos \widehat {AMC}\)
Hay \(\cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
b) Áp dụng định lí cos trong tam giác AMB ta có:
\(\begin{array}{l}A{B^2} = M{A^2} + M{B^2} - 2MA.MB\;\cos \widehat {AMB}\\ \Leftrightarrow M{A^2} + M{B^2} - A{B^2} = 2MA.MB\;\cos \widehat {AMB}\;\;(1)\end{array}\)
Tương tự, Áp dụng định lí cos trong tam giác AMB ta được:
\(\begin{array}{l}A{C^2} = M{A^2} + M{C^2} - 2MA.MC\;\cos \widehat {AMC}\\ \Leftrightarrow M{A^2} + M{C^2} - A{C^2} = 2MA.MC\;\cos \widehat {AMC}\;\;(2)\end{array}\)
c) Từ (1), suy ra \(M{A^2} = A{B^2} - M{B^2} + 2MA.MB\;\cos \widehat {AMB}\;\)
Từ (2), suy ra \(M{A^2} = A{C^2} - M{C^2} + 2MA.MC\;\cos \widehat {AMC}\;\)
Cộng vế với vế ta được:
\(2M{A^2} = \left( {A{B^2} - M{B^2} + 2MA.MB\;\cos \widehat {AMB}} \right)\; + \left( {A{C^2} - M{C^2} + 2MA.MC\;\cos \widehat {AMC}} \right)\;\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - M{B^2} - M{C^2} + 2MA.MB\;\cos \widehat {AMB} + 2MA.MC\;\cos \widehat {AMC}\)
Mà: \(MB = MC = \frac{{BC}}{2}\) (do AM là trung tuyến)
\( \Rightarrow 2M{A^2} = A{B^2} + A{C^2} - {\left( {\frac{{BC}}{2}} \right)^2} - {\left( {\frac{{BC}}{2}} \right)^2} + 2MA.MB\;\cos \widehat {AMB} + 2MA.MB\;\cos \widehat {AMC}\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - 2.{\left( {\frac{{BC}}{2}} \right)^2} + 2MA.MB\;\left( {\cos \widehat {AMB} + \;\cos \widehat {AMC}} \right)\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - {\frac{{BC}}{2}^2}\)
\(\begin{array}{l} \Leftrightarrow M{A^2} = \frac{{A{B^2} + A{C^2} - {{\frac{{BC}}{2}}^2}}}{2}\\ \Leftrightarrow M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\end{array}\) (đpcm)
Cách 2:
Theo ý a, ta có: \(\cos \widehat {AMC} = - \cos \widehat {AMB}\)
Từ đẳng thức (1): suy ra \(\cos \widehat {AMB} = \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}\)
\( \Rightarrow \cos \widehat {AMC} = - \cos \widehat {AMB} = - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}\)
Thế \(\cos \widehat {AMC}\)vào biểu thức (2), ta được:
\(M{A^2} + M{C^2} - A{C^2} = 2MA.MC.\left( { - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}} \right)\)
Lại có: \(MB = MC = \frac{{BC}}{2}\) (do AM là trung tuyến)
\(\begin{array}{l} \Rightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} = 2MA.MB.\left( { - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}} \right)\\ \Leftrightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} = - \left( {M{A^2} + M{B^2} - A{B^2}} \right)\\ \Leftrightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} + M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{B^2} = 0\\ \Leftrightarrow 2M{A^2} - A{B^2} - A{C^2} + {\frac{{BC}}{2}^2} = 0\\ \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - {\frac{{BC}}{2}^2}\\ \Leftrightarrow M{A^2} = \frac{{A{B^2} + A{C^2} - {{\frac{{BC}}{2}}^2}}}{2}\\ \Leftrightarrow M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\end{array}\)
Bài 3.16 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và ứng dụng vào giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết bài tập này:
Đề bài:
Cho hàm số y = f(x) = 2x + 3.
a) Tính f(0); f(1); f(-1); f(2).
b) Tìm x sao cho f(x) = 5; f(x) = -1.
Lời giải:
a) Để tính f(0), f(1), f(-1), f(2), ta thay các giá trị của x vào hàm số y = f(x) = 2x + 3:
b) Để tìm x sao cho f(x) = 5, ta giải phương trình:
2x + 3 = 5
2x = 5 - 3
2x = 2
x = 1
Để tìm x sao cho f(x) = -1, ta giải phương trình:
2x + 3 = -1
2x = -1 - 3
2x = -4
x = -2
Kết luận:
a) f(0) = 3; f(1) = 5; f(-1) = 1; f(2) = 7.
b) x = 1 khi f(x) = 5; x = -2 khi f(x) = -1.
Giải thích chi tiết:
Bài tập này yêu cầu học sinh hiểu rõ cách tính giá trị của hàm số tại một điểm cho trước và cách tìm giá trị của x khi biết giá trị của hàm số. Để giải bài tập này, học sinh cần nắm vững định nghĩa của hàm số bậc nhất và các phép toán cơ bản.
Mở rộng:
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các hằng số. Hàm số bậc nhất có đồ thị là một đường thẳng. Hệ số a được gọi là hệ số góc của đường thẳng, nó xác định độ dốc của đường thẳng. Hệ số b được gọi là tung độ gốc, nó là tung độ của điểm mà đường thẳng cắt trục Oy.
Các bài tập tương tự:
Để luyện tập thêm, các em có thể làm các bài tập tương tự trong SGK Toán 10 tập 1 – Kết nối tri thức hoặc trên các trang web học Toán online khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và kỹ năng giải bài tập.
Lưu ý:
Khi giải bài tập về hàm số bậc nhất, các em cần chú ý đến các điều kiện của bài toán và lựa chọn phương pháp giải phù hợp. Ngoài ra, các em cũng nên kiểm tra lại kết quả của mình để đảm bảo tính chính xác.
Hy vọng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài 3.16 trang 44 SGK Toán 10 tập 1 – Kết nối tri thức. Chúc các em học tập tốt!
Ví dụ minh họa:
Giả sử ta có hàm số y = 3x - 2. Hãy tính f(4) và tìm x sao cho f(x) = 7.
f(4) = 3 * 4 - 2 = 10
Để tìm x sao cho f(x) = 7, ta giải phương trình:
3x - 2 = 7
3x = 9
x = 3
Tổng kết:
Bài tập về hàm số bậc nhất là một phần quan trọng trong chương trình Toán 10. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp các em học tốt môn Toán và chuẩn bị cho các bài học tiếp theo.
Các nguồn tài liệu tham khảo: