Chào mừng bạn đến với bài học về Lý thuyết Tích của Vectơ mới một số trong chương trình Toán 10 Kết nối tri thức tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn kiến thức cơ bản và quan trọng về tích của hai vectơ, một khái niệm nền tảng trong hình học vectơ.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, và các ứng dụng thực tế của tích của vectơ, giúp bạn giải quyết các bài toán một cách hiệu quả và chính xác.
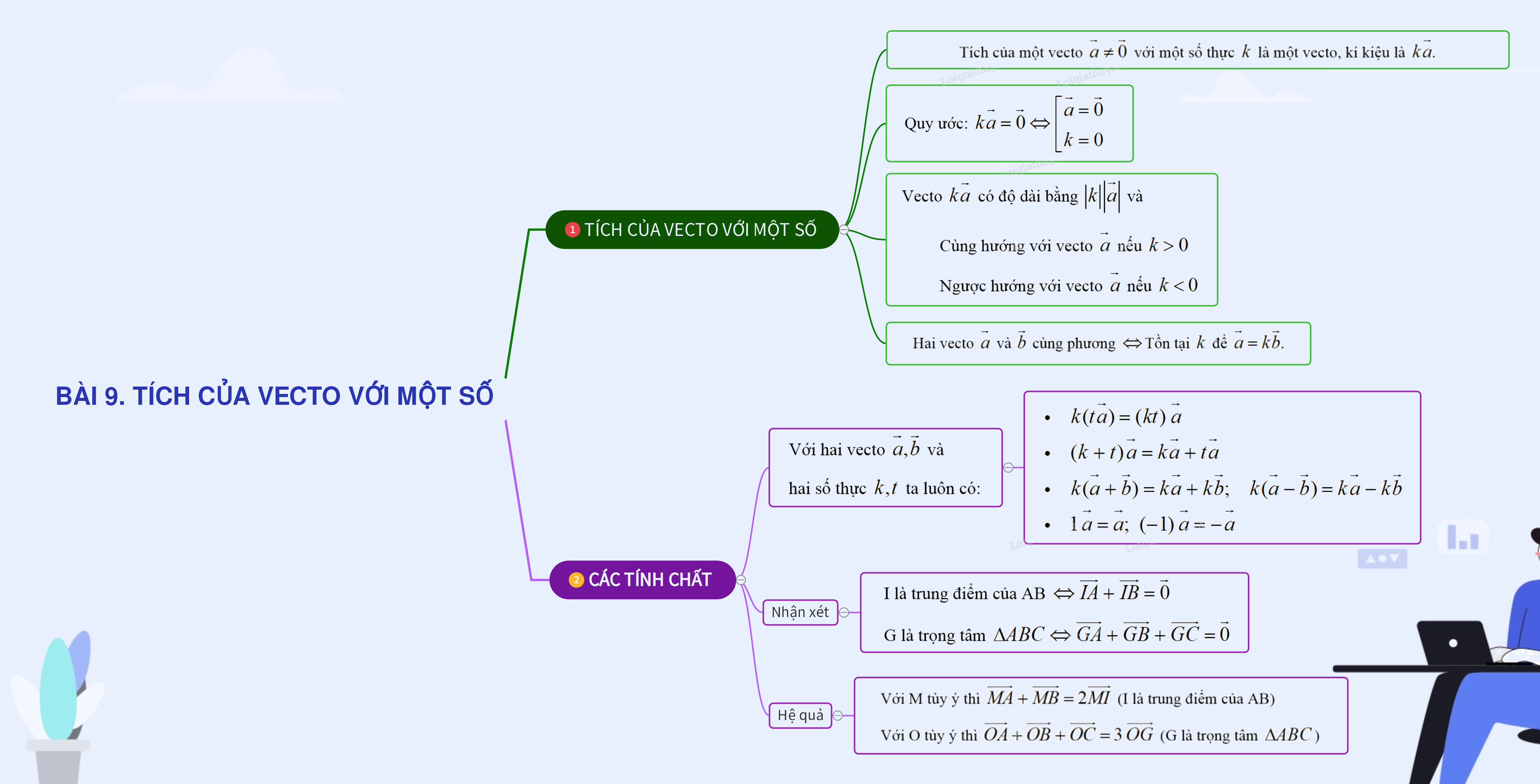
1. TÍCH CỦA VECTO VỚI MỘT SỐ 2. CÁC TÍNH CHẤT CỦA PHÉP NHÂN VECTƠ VỚI MỘT SỐ
1. TÍCH CỦA VECTO VỚI MỘT SỐ
+) Tích của một vecto \(\overrightarrow a \ne \overrightarrow 0 \) với một số thực \(k\) là một vecto, kí kiệu là \(k\overrightarrow a .\)
+) Vecto \(k\overrightarrow a \) có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\) và
Cùng hướng với vecto \(\overrightarrow a \) nếu \(k > 0\)
Ngược hướng với vecto \(\overrightarrow a \) nếu \(k < 0\)
+) Quy ước: \(k\overrightarrow a = \overrightarrow 0 \Leftrightarrow \left[ \begin{array}{l}\overrightarrow a = \overrightarrow 0 \\k = 0\end{array} \right.\)
Nhận xét: Hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương khi và chỉ khi tồn tại \(k\) để \(\overrightarrow a = k\overrightarrow b .\)
2. CÁC TÍNH CHẤT CỦA PHÉP NHÂN VECTƠ VỚI MỘT SỐ
+) Với hai vecto \(\overrightarrow a ,\overrightarrow b \) và hai số thực \(k,t\) ta luôn có:
\(\begin{array}{l}k(t\overrightarrow a ) = (kt)\;\overrightarrow a \\(k + t)\,\overrightarrow a = k\overrightarrow a + t\overrightarrow a \\k(\overrightarrow a + \overrightarrow b ) = k\overrightarrow a + k\overrightarrow b ;\quad k(\overrightarrow a - \overrightarrow b ) = k\overrightarrow a - k\overrightarrow b \\1\;\overrightarrow a = \overrightarrow a ;\;\;( - 1)\;\overrightarrow a = - \,\overrightarrow a \end{array}\)
+) Nhận xét:
I là trung điểm của AB \( \Leftrightarrow \overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \)
G là trọng tâm \(\Delta ABC \Leftrightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
+) Hệ quả
Với M tùy ý thì \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \) (I là trung điểm của AB)
Với O tùy ý thì \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\;\overrightarrow {OG} \) (G là trọng tâm \(\Delta ABC\))
Tích của hai vectơ là một khái niệm quan trọng trong hình học vectơ, đóng vai trò then chốt trong việc giải quyết nhiều bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ, và các ứng dụng trong vật lý.
Cho hai vectơ a và b khác 0. Tích của hai vectơ a và b, ký hiệu là a.b, là một số thực được xác định bởi công thức:
a.b = |a||b|cos(θ)
Trong đó:
Tích của hai vectơ có những tính chất quan trọng sau:
Có một số trường hợp đặc biệt cần lưu ý:
Tích của vectơ có nhiều ứng dụng trong toán học và vật lý, bao gồm:
Để hiểu rõ hơn về lý thuyết tích của vectơ, hãy cùng giải một số bài tập vận dụng:
Lý thuyết tích của vectơ là một công cụ mạnh mẽ trong hình học vectơ, giúp chúng ta giải quyết nhiều bài toán một cách hiệu quả. Việc nắm vững định nghĩa, tính chất, và các ứng dụng của tích của vectơ là rất quan trọng để học tốt môn Toán 10 Kết nối tri thức.