Bài 4.38 trang 72 SGK Toán 10 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các em hiểu rõ bản chất của vấn đề.
Cho ba vectơ a, b, u với |a|=1, |b|=1 và a vuông góc với b. Xét một hệ trục Oxy với các vectơ đơn vị i=a,j=b. Chứng minh rằng: a) Vectơ u có tọa độ là (u.a; u.b) b) u= (u.a).a +(u.b).b
Đề bài
Cho ba vectơ \(\overrightarrow a ,\;\overrightarrow b ,\;\overrightarrow u \) với \(|\overrightarrow a |\; = \;\,|\overrightarrow b |\; = 1\) và \(\overrightarrow a \bot \overrightarrow b \). Xét một hệ trục Oxy với các vectơ đơn vị \(\overrightarrow i = \overrightarrow a ,\;\overrightarrow j = \overrightarrow b .\) Chứng minh rằng:
a) Vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)
b) \(\overrightarrow u = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow a + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow b \)
Phương pháp giải - Xem chi tiết
a) Trên hệ trục Oxy mới, xác định hoành độ, tung độ của vectơ \(\overrightarrow u \)
+) \(\overrightarrow u \,.\,\overrightarrow a = |\overrightarrow u| \,.\,|\overrightarrow a|. \cos (\overrightarrow u \,.\,\overrightarrow a) \)
b) Vectơ \(\overrightarrow u \) có tọa độ \((x\,;y)\) trong hệ trục Oxy với các vectơ đơn vị \(\overrightarrow i ;\;\overrightarrow j \) thì \(\overrightarrow u = x\,.\,\overrightarrow i + y.\,\overrightarrow j \)
Lời giải chi tiết
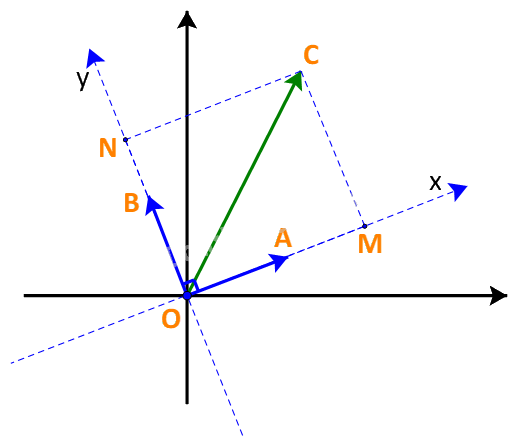
a) Trên mặt phẳng tọa độ, lấy các điểm A, B, C sao cho \(\overrightarrow {OA} = \overrightarrow a ;\;\overrightarrow {OB} = \overrightarrow b ;\;\overrightarrow {OC} = \overrightarrow u \)
Trên hệ trục Oxy với các vectơ đơn vị \(\overrightarrow i = \overrightarrow a ,\;\overrightarrow j = \overrightarrow b \), lấy M, N là hình chiếu của C trên Ox, Oy.
Gọi tọa độ của \(\overrightarrow u \)là \(\left( {x;y} \right)\). Đặt \(\alpha = \left( {\overrightarrow u ,\overrightarrow a } \right)\).
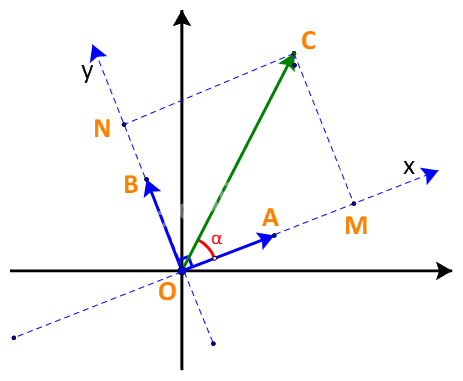
+) Nếu \({0^o} < \alpha < {90^o}\): \(x = OM = \;|\overrightarrow u |.\cos \alpha = \;|\overrightarrow u |.\cos \alpha .\;|\overrightarrow a |\; = \overrightarrow u \,.\,\overrightarrow a \,;\)
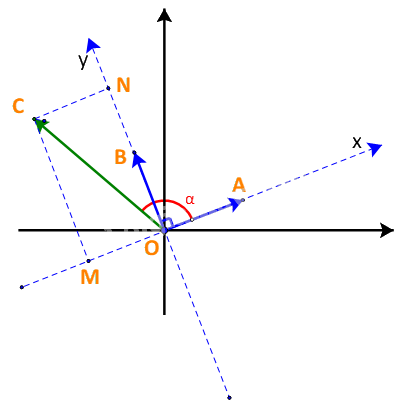
+) Nếu \({90^o} < \alpha < {180^o}\): \(x = - OM = \; - |\overrightarrow u |.\cos ({180^o} - \alpha ) = \;|\overrightarrow u |.\cos \alpha \; = \overrightarrow u \,.\,\overrightarrow a \,;\)
Như vậy ta luôn có: \(x = \overrightarrow u .\overrightarrow a \)
Chứng minh tương tự, ta có: \(y = \overrightarrow u .\overrightarrow b \)
Vậy vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)
b) Trong hệ trục Oxy với các vectơ vectơ đơn vị \(\overrightarrow i = \overrightarrow a ,\;\overrightarrow j = \overrightarrow b \), vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)
\(\begin{array}{l} \Rightarrow \overrightarrow u = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow i + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow j \\ \Leftrightarrow \overrightarrow u = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow a + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow b \end{array}\)
Bài 4.38 trang 72 SGK Toán 10 – Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về vectơ để chứng minh một số tính chất hình học. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài, xác định rõ yêu cầu và tìm hướng giải phù hợp. Thông thường, các bài tập về vectơ trong hình học yêu cầu chúng ta:
Đề bài: (Nội dung đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho hình bình hành ABCD. Gọi M là trung điểm của BC. Chứng minh rằng AM và BD cắt nhau tại một điểm.)
Lời giải:
1. Chọn hệ tọa độ: Chọn hệ tọa độ Oxy với gốc O trùng với điểm A, trục Ox trùng với đường thẳng AB, trục Oy trùng với đường thẳng AD. Giả sử tọa độ các điểm là:
2. Tìm vectơ:
3. Tìm giao điểm: Giả sử giao điểm của AM và BD là I. Khi đó, tồn tại số t sao cho AI = t.AM và tồn tại số s sao cho BI = s.BD.
Suy ra:
Đồng nhất tọa độ, ta có:
Từ phương trình thứ hai, ta có t = 2s. Thay vào phương trình thứ nhất, ta được 2sa = a - sa, suy ra 3sa = a, hay s = 1/3. Do đó, t = 2/3.
Vậy, I = (2a/3; b/3). Điều này chứng tỏ AM và BD cắt nhau tại một điểm.
Để giải bài tập về vectơ một cách hiệu quả, bạn cần lưu ý những điều sau:
Để củng cố kiến thức về vectơ, bạn có thể tham khảo thêm các bài tập tương tự trong SGK Toán 10 – Kết nối tri thức và các tài liệu ôn tập khác.
Giaitoan.edu.vn hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về bài 4.38 trang 72 SGK Toán 10 – Kết nối tri thức và tự tin giải các bài tập tương tự.