Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 74, 75, 76 sách giáo khoa Toán 10 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Trong HĐ2, Hòa dùng kính lúp để quan sát mực nước trên ống đo thứ hai được hình ảnh như Hình 5.2 Một phép đo đường kính nhân tế bào cho kết quả là. Đường kính thực của nhân tế bào thuộc đoạn nào? Công ty (trong Ví dụ 2) cũng sử dụng dây chuyền B để đóng gạo với khối lượng chính Đánh giá sai số tương đối của khối lượng bao gạo được đóng gói theo hai dây chuyền A, B ở Ví dụ 2 và HĐ4. Dựa trên tiêu chí này, dây chuyền nào tốt hơn?
Một phép đo đường kính nhân tế bào cho kết quả là \(5 \pm 0,3\mu m\). Đường kính thực của nhân tế bào thuộc đoạn nào?
Phương pháp giải:
Ta viết \(\bar a = a \pm d\) thì có nghĩa là số đúng \(\bar a\) nằm trong đoạn \(\left[ {a - d;a + d} \right]\).
Với a là số gần đúng của \(\bar a\) và d là độ chính xác của \(\bar a\).
Lời giải chi tiết:
Gọi \(\bar a\) là đường kính thực của nhân tế bào.
Vì phép đo đường kính nhân tế bào cho kết quả là \(5 \pm 0,3\mu m\).
=> \(a = 5\mu m;d = 0,3\mu m\)
Nên ta có \(\bar a\) nằm trong đoạn \(\left[ {5 - 0,3;5 + 0,3} \right]\) hay \(\left[ {4,7;5,3} \right]\).
Đánh giá sai số tương đối của khối lượng bao gạo được đóng gói theo hai dây chuyền A, B ở Ví dụ 2 và HĐ4. Dựa trên tiêu chí này, dây chuyền nào tốt hơn?
Phương pháp giải:
- Đánh giá sai số tương đối: \({\delta _a} \le \frac{d}{{\left| a \right|}}\)
Với d là độ chính xác và a là số gần đúng.
- Nhận xét dây chuyền nào tốt hơn: \(\frac{d}{{\left| a \right|}}\) càng nhỏ thì chất lượng phép đo hay tính toán càng cao.
Lời giải chi tiết:
Xét dây chuyền A: ta có d=0,2; a=5.
\({\delta _5} \le \frac{{0,2}}{{\left| 5 \right|}} = 0,04 = 4\% \)
Xét dây chuyền B: ta có d=0,5; a=20
\({\delta _5} \le \frac{{0,5}}{{\left| {20} \right|}} = 0,025 = 2,5\% \)
Ta thấy \(2,5\% < 4\% \) nên dây chuyền B tốt hơn.
Chú ý
Có thể không cần đổi sang đơn vị phần trăm (%) để so sánh.
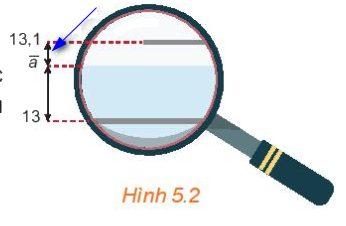
Trong HĐ2, Hòa dùng kính lúp để quan sát mực nước trên ống đo thứ hai được hình ảnh như Hình 5.2. Kí hiệu \(\overline a \)(\(c{m^3}\)) là số đo thể tích của nước.
Quan sát hình vẽ để so sánh \(\left| {13 - \bar a} \right|\) và \(\left| {13,1 - \bar a} \right|\) rồi cho biết trong hai số đo thể tích \(13c{m^3}\) và \(13,1c{m^3}\), số đo nào gần với thể tích của cốc nước hơn.
Phương pháp giải:
Quan sát hình vẽ 5.2 và kiểm tra giữa hai số 13,1 và 13, số nào gần \(\bar a\) hơn.
Lời giải chi tiết:
Ta quan sát hình trên thì thấy số 13,1 gần \(\bar a\) hơn.

Công ty (trong Ví dụ 2) cũng sử dụng dây chuyền B để đóng gạo với khối lượng chính xác là 20 kg. Trên bao bì ghi thông tin khối lượng là \(20 \pm 0,5\) kg.
Khẳng định “Dây chuyền A tốt hơn dây chuyền B" là đúng hay sai?
Lời giải chi tiết:
Mặc dù độ chính xác của khối lượng bao gạo đóng bằng dây chuyền A nhỏ hơn nhưng do bao gạo đóng bằng dây chuyền B nặng hơn nhiều nên ta không dựa vào sai số tuyệt đối để so sánh.
Do đó câu hỏi này ta chưa thể trả lời chính xác được nếu chỉ dựa vào các kiến thức đã học trước đó.
Xem thêm bài Luyện tập 3 trang 76 Sách giáo khoa Toán 10 – Kết nối tri thức với cuộc sống.
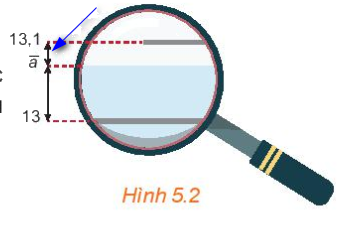
Trong HĐ2, Hòa dùng kính lúp để quan sát mực nước trên ống đo thứ hai được hình ảnh như Hình 5.2. Kí hiệu \(\overline a \)(\(c{m^3}\)) là số đo thể tích của nước.
Quan sát hình vẽ để so sánh \(\left| {13 - \bar a} \right|\) và \(\left| {13,1 - \bar a} \right|\) rồi cho biết trong hai số đo thể tích \(13c{m^3}\) và \(13,1c{m^3}\), số đo nào gần với thể tích của cốc nước hơn.
Phương pháp giải:
Quan sát hình vẽ 5.2 và kiểm tra giữa hai số 13,1 và 13, số nào gần \(\bar a\) hơn.
Lời giải chi tiết:
Ta quan sát hình trên thì thấy số 13,1 gần \(\bar a\) hơn.
Một phép đo đường kính nhân tế bào cho kết quả là \(5 \pm 0,3\mu m\). Đường kính thực của nhân tế bào thuộc đoạn nào?
Phương pháp giải:
Ta viết \(\bar a = a \pm d\) thì có nghĩa là số đúng \(\bar a\) nằm trong đoạn \(\left[ {a - d;a + d} \right]\).
Với a là số gần đúng của \(\bar a\) và d là độ chính xác của \(\bar a\).
Lời giải chi tiết:
Gọi \(\bar a\) là đường kính thực của nhân tế bào.
Vì phép đo đường kính nhân tế bào cho kết quả là \(5 \pm 0,3\mu m\).
=> \(a = 5\mu m;d = 0,3\mu m\)
Nên ta có \(\bar a\) nằm trong đoạn \(\left[ {5 - 0,3;5 + 0,3} \right]\) hay \(\left[ {4,7;5,3} \right]\).

Công ty (trong Ví dụ 2) cũng sử dụng dây chuyền B để đóng gạo với khối lượng chính xác là 20 kg. Trên bao bì ghi thông tin khối lượng là \(20 \pm 0,5\) kg.
Khẳng định “Dây chuyền A tốt hơn dây chuyền B" là đúng hay sai?
Lời giải chi tiết:
Mặc dù độ chính xác của khối lượng bao gạo đóng bằng dây chuyền A nhỏ hơn nhưng do bao gạo đóng bằng dây chuyền B nặng hơn nhiều nên ta không dựa vào sai số tuyệt đối để so sánh.
Do đó câu hỏi này ta chưa thể trả lời chính xác được nếu chỉ dựa vào các kiến thức đã học trước đó.
Xem thêm bài Luyện tập 3 trang 76 Sách giáo khoa Toán 10 – Kết nối tri thức với cuộc sống.
Đánh giá sai số tương đối của khối lượng bao gạo được đóng gói theo hai dây chuyền A, B ở Ví dụ 2 và HĐ4. Dựa trên tiêu chí này, dây chuyền nào tốt hơn?
Phương pháp giải:
- Đánh giá sai số tương đối: \({\delta _a} \le \frac{d}{{\left| a \right|}}\)
Với d là độ chính xác và a là số gần đúng.
- Nhận xét dây chuyền nào tốt hơn: \(\frac{d}{{\left| a \right|}}\) càng nhỏ thì chất lượng phép đo hay tính toán càng cao.
Lời giải chi tiết:
Xét dây chuyền A: ta có d=0,2; a=5.
\({\delta _5} \le \frac{{0,2}}{{\left| 5 \right|}} = 0,04 = 4\% \)
Xét dây chuyền B: ta có d=0,5; a=20
\({\delta _5} \le \frac{{0,5}}{{\left| {20} \right|}} = 0,025 = 2,5\% \)
Ta thấy \(2,5\% < 4\% \) nên dây chuyền B tốt hơn.
Chú ý
Có thể không cần đổi sang đơn vị phần trăm (%) để so sánh.
Mục 2 của chương trình Toán 10 tập 1 - Kết nối tri thức tập trung vào các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp, và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên. Bài viết này sẽ đi sâu vào giải chi tiết từng bài tập trong mục 2, trang 74, 75, 76 của sách giáo khoa, giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải toán.
Bài tập này yêu cầu các em xác định các phần tử thuộc một tập hợp cho trước, dựa trên một điều kiện nhất định. Để giải bài tập này, các em cần hiểu rõ khái niệm về tập hợp và cách xác định các phần tử của tập hợp.
Bài tập này yêu cầu các em thực hiện các phép toán trên tập hợp, như hợp, giao, hiệu, và phần bù của tập hợp. Để giải bài tập này, các em cần hiểu rõ định nghĩa và tính chất của các phép toán trên tập hợp.
Bài tập này yêu cầu các em chứng minh các tính chất của tập hợp, như tính giao hoán, tính kết hợp, tính phân phối của các phép toán trên tập hợp. Để giải bài tập này, các em cần sử dụng các định nghĩa và tính chất của tập hợp để chứng minh.
Ngoài các bài tập cơ bản về tập hợp, còn có một số dạng bài tập thường gặp khác, như:
Để giải bài tập về tập hợp hiệu quả, các em có thể áp dụng một số mẹo sau:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải các bài tập trong mục 2 trang 74, 75, 76 SGK Toán 10 tập 1 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Tập hợp | Ký hiệu | Định nghĩa |
|---|---|---|
| Tập hợp các số tự nhiên | N | {0, 1, 2, 3,...} |
| Tập hợp các số nguyên | Z | {..., -2, -1, 0, 1, 2,...} |
| Tập hợp các số hữu tỉ | Q | {a/b | a, b ∈ Z, b ≠ 0} |