Bài 9 trang 96 SGK Toán 10 Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học phẳng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9 trang 96 SGK Toán 10 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.
Đề bài
Cho hàm số \(y = f(x) = a{x^2} + bx + c\) với đồ thị là parabol (P) có đỉnh \(I\left( {\frac{5}{2}; - \frac{1}{4}} \right)\) và đi qua điểm \(A(1;2)\)
a) Biết rằng phương trình của parabol có thể viết dưới dạng \(y = a{(x - h)^2} + k\), tron đó I(h;k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.
b) Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f(x)\)
c) Giải bất phương trình \(f(x) \ge 0\)
Lời giải chi tiết
a) Parabol: \(y = a{(x - h)^2} + k\) với \(I(h;k) = \left( {\frac{5}{2}; - \frac{1}{4}} \right)\) là tọa độ đỉnh.
\( \Rightarrow y = a{\left( {x - \frac{5}{2}} \right)^2} - \frac{1}{4}\)
(P) đi qua \(A(1;2)\) nên \(2 = a{\left( {1 - \frac{5}{2}} \right)^2} - \frac{1}{4} \Rightarrow a = 1\)
\( \Rightarrow y = {\left( {x - \frac{5}{2}} \right)^2} - \frac{1}{4} \Leftrightarrow y = {x^2} - 5x + 6\)
Vậy parabol đó là \(y = {x^2} - 5x + 6\)
b) Vẽ parabol \(y = {x^2} - 5x + 6\)
+ Đỉnh \(I\left( {\frac{5}{2}; - \frac{1}{4}} \right)\)
+ Giao với Oy tại điểm \((0;6)\)
+ Giao với Ox tại điểm \((3;0)\) và \((2;0)\)
+ Trục đối xứng \(x = \frac{5}{2}\). Điểm đối xứng với điểm \((0;6)\) qua trục đối xứng có tọa độ \((5;6)\)
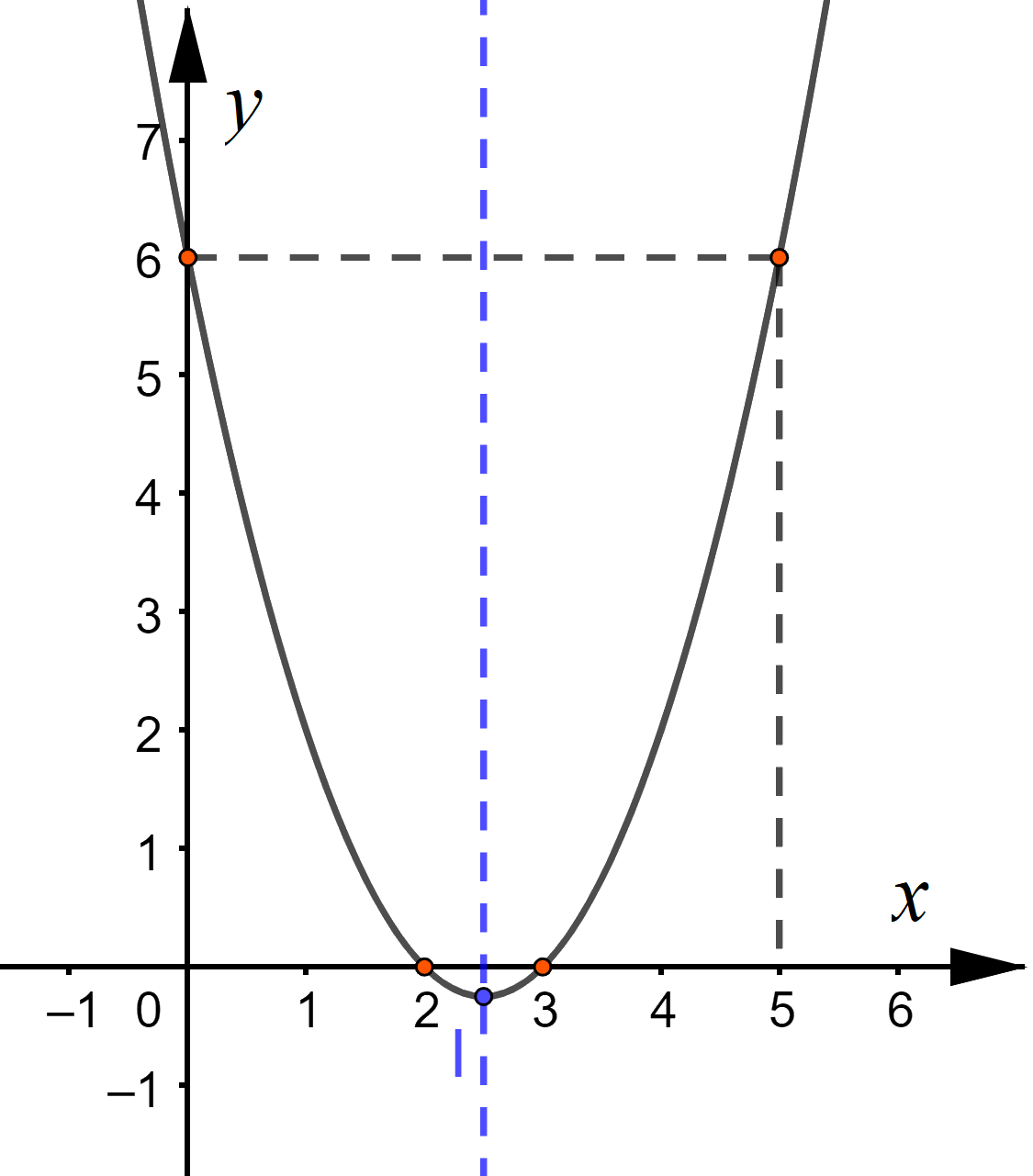
b) Hàm số đồng biến trên khoảng \(\left( { - \frac{5}{2}; + \infty } \right)\)
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - \frac{5}{2}} \right)\)
c) \(f(x) \ge 0 \Leftrightarrow {x^2} - 5x + 6 \ge 0\)
Cách 1: Quan sát đồ thị, ta thấy các điểm có\(y \ge 0\) ứng với hoành độ \(x \in ( - \infty ;2] \cup [3; + \infty )\)
Do đó tập nghiệm của BPT \(f(x) \ge 0\) là \(S = ( - \infty ;2] \cup [3; + \infty )\)
Cách 2:
\(\begin{array}{l} \Leftrightarrow {x^2} - 5x + 6 \ge 0\\ \Leftrightarrow (x - 2)(x - 3) \ge 0\end{array}\)
Do đó \(x - 2\) và \(x - 3\) cùng dấu. Mà \(x - 2 > x - 3\;\forall x \in \mathbb{R}\)
\( \Leftrightarrow \left[ \begin{array}{l}x - 3 \ge 0\\x - 2 \le 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 3\\x \le 2\end{array} \right.\)
Tập nghiệm của BPT là \(S = ( - \infty ;2] \cup [3; + \infty )\)
Bài 9 trang 96 SGK Toán 10 – Kết nối tri thức thuộc chương 4: Vectơ trong mặt phẳng. Bài tập này tập trung vào việc áp dụng các tính chất của vectơ, đặc biệt là các phép toán cộng, trừ vectơ và tích của một số với vectơ để chứng minh các đẳng thức vectơ và giải quyết các bài toán hình học.
Bài 9 trang 96 SGK Toán 10 – Kết nối tri thức thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 9 trang 96 SGK Toán 10 – Kết nối tri thức. (Lưu ý: Nội dung chi tiết lời giải sẽ được trình bày cụ thể cho từng câu hỏi trong bài tập. Do giới hạn độ dài, chúng ta sẽ tập trung vào phương pháp chung và các lưu ý quan trọng.)
Để giải tốt các bài tập về vectơ, các em cần nắm vững các kiến thức sau:
Ví dụ 1: Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng OA = OC.
Lời giải:
Vì ABCD là hình bình hành nên AB = DC và AB // DC. Do đó, ABDC là hình bình hành. Suy ra OA = OC (tính chất đường chéo của hình bình hành).
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, các em có thể tham khảo thêm các bài tập sau:
Bài 9 trang 96 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng giúp các em học sinh hiểu sâu hơn về vectơ và ứng dụng của nó trong hình học. Hy vọng với lời giải chi tiết và phương pháp giải bài tập mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn khi giải các bài tập về vectơ.
| Khái niệm | Mô tả |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Phép cộng vectơ | Quy tắc hình bình hành hoặc quy tắc tam giác. |
| Tích của một số với vectơ | Làm thay đổi độ dài của vectơ. |