Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn cách giải bài 2.6 trang 30 SGK Toán 10 tập 1 – Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những phương pháp giải toán đơn giản, dễ tiếp thu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6 kg thịt bò và 1,1 kg thịt lợn, giá tiền 1 kg thịt bò là 250 nghìn đồng, 1 kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.
c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.
Phương pháp giải:
Bước 1: Xác định giá trị của F tại các điểm thuộc miền đa giác biểu diễn miền nghiệm của hệ bất phương trình ở câu a.
Bước 2: Giá trị lớn nhất của F là số lớn nhất trong các số tìm được ở bước 1.
Lời giải chi tiết:
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.\)
Ta có F(1,6;0,2)=250.1,6+160.0,2=432.
F(1,6;1,1)=250.1,6+160.1,1=576
F(0,3;1,1)=251
F(0,6;0,7)=262
Giá trị nhỏ nhất là F(0,3;1,1)=251.
Vậy để chi phí ít nhất thì cần mua 0,3kg thịt bò và 1,1 thịt lợn.
b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy
biểu diễn F theo x và y.
Phương pháp giải:
Dựa vào số tiền mỗi kg thịt lợn và thịt bò để lập biểu thức.
Lời giải chi tiết:
Vì số tiền mỗi kg thịt bò và thịt lợn lần lượt là 250 nghìn đồng và 160 nghìn đồng nên ta có
\(F\left( {x;y} \right) = 250x + 160y\)(nghìn đồng)
a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương
trình rồi xác định miền nghiệm của hệ đó.
Phương pháp giải:
Dựa vào:
+ Số đơn vị tối thiểu của Protein
+ Số đơn vị tối thiểu của Lipit
+ Số kg tối đa thịt bò
+ Số kg tối đa thịt lợn.
Lời giải chi tiết:
Thịt bò | Thịt lợn | |
Protein | 800/1kg | 600/1kg |
Lipit | 200/1kg | 400/1kg |
a) Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.
Số lượng thịt bò và thịt lợn phải là một số không âm nên ta có: \(x \ge 0,y \ge 0\).
Một gia đình cần ít nhất 900 đơn vị protein trong thức ăn mỗi ngày nên ta có: \(800x + 600y \ge 900 \Leftrightarrow 8x + 6y \ge 9\)
Một gia đình cần ít nhất 400 đơn vị protein trong thức ăn mỗi ngày nên ta có: \(200x + 400y \ge 400 \Leftrightarrow x + 2y \ge 2\)
Vì gia đình này chỉ mua nhiều nhất là 1,6 kg thịt bò và 1,1 kg thịt lợn nên ta có:
\(x \le 1,6\) và \(y \le 1,1\).
Vậy ta có hệ: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.\)
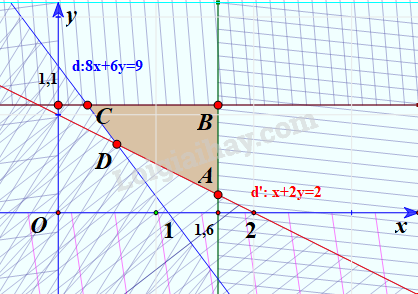
Miền nghiệm của hệ là tứ giác ABCD với
A(1,6;0,2) (giao của d’ và đường thẳng x=1,6)
B(1,6;1,1) (giao của đường thẳng x=1,6 và đường thẳng y=1,1)
C(0,3;1,1) (giao của d và đường thẳng y=1,1)
D(0,6;0,7) (giao của d và d’)
b) Vì số tiền mỗi kg thịt bò và thịt lợn lần lượt là 250 nghìn đồng và 160 nghìn đồng nên ta có
\(F\left( {x;y} \right) = 250x + 160y\)(nghìn đồng)
c)
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.\)
Ta có F(1,6;0,2)=250.1,6+160.0,2=432.
F(1,6;1,1)=250.1,6+160.1,1=576
F(0,3;1,1)=251
F(0,6;0,7)=262
Giá trị nhỏ nhất là F(0,3;1,1)=251.
Vậy để chi phí ít nhất thì cần mua 0,3kg thịt bò và 1,1 thịt lợn.
Chú ý
Đơn vị của F phải là nghìn đồng.
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6 kg thịt bò và 1,1 kg thịt lợn, giá tiền 1 kg thịt bò là 250 nghìn đồng, 1 kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.
a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương
trình rồi xác định miền nghiệm của hệ đó.
Phương pháp giải:
Dựa vào:
+ Số đơn vị tối thiểu của Protein
+ Số đơn vị tối thiểu của Lipit
+ Số kg tối đa thịt bò
+ Số kg tối đa thịt lợn.
Lời giải chi tiết:
Thịt bò | Thịt lợn | |
Protein | 800/1kg | 600/1kg |
Lipit | 200/1kg | 400/1kg |
a) Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.
Số lượng thịt bò và thịt lợn phải là một số không âm nên ta có: \(x \ge 0,y \ge 0\).
Một gia đình cần ít nhất 900 đơn vị protein trong thức ăn mỗi ngày nên ta có: \(800x + 600y \ge 900 \Leftrightarrow 8x + 6y \ge 9\)
Một gia đình cần ít nhất 400 đơn vị protein trong thức ăn mỗi ngày nên ta có: \(200x + 400y \ge 400 \Leftrightarrow x + 2y \ge 2\)
Vì gia đình này chỉ mua nhiều nhất là 1,6 kg thịt bò và 1,1 kg thịt lợn nên ta có:
\(x \le 1,6\) và \(y \le 1,1\).
Vậy ta có hệ: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.\)
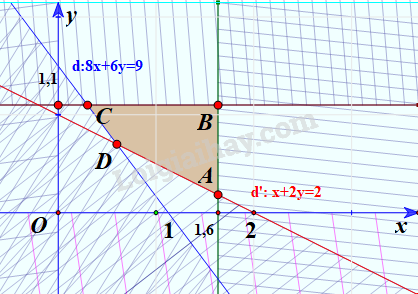
Miền nghiệm của hệ là tứ giác ABCD với
A(1,6;0,2) (giao của d’ và đường thẳng x=1,6)
B(1,6;1,1) (giao của đường thẳng x=1,6 và đường thẳng y=1,1)
C(0,3;1,1) (giao của d và đường thẳng y=1,1)
D(0,6;0,7) (giao của d và d’)
b) Vì số tiền mỗi kg thịt bò và thịt lợn lần lượt là 250 nghìn đồng và 160 nghìn đồng nên ta có
\(F\left( {x;y} \right) = 250x + 160y\)(nghìn đồng)
c)
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.\)
Ta có F(1,6;0,2)=250.1,6+160.0,2=432.
F(1,6;1,1)=250.1,6+160.1,1=576
F(0,3;1,1)=251
F(0,6;0,7)=262
Giá trị nhỏ nhất là F(0,3;1,1)=251.
Vậy để chi phí ít nhất thì cần mua 0,3kg thịt bò và 1,1 thịt lợn.
Chú ý
Đơn vị của F phải là nghìn đồng.
b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy
biểu diễn F theo x và y.
Phương pháp giải:
Dựa vào số tiền mỗi kg thịt lợn và thịt bò để lập biểu thức.
Lời giải chi tiết:
Vì số tiền mỗi kg thịt bò và thịt lợn lần lượt là 250 nghìn đồng và 160 nghìn đồng nên ta có
\(F\left( {x;y} \right) = 250x + 160y\)(nghìn đồng)
c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.
Phương pháp giải:
Bước 1: Xác định giá trị của F tại các điểm thuộc miền đa giác biểu diễn miền nghiệm của hệ bất phương trình ở câu a.
Bước 2: Giá trị lớn nhất của F là số lớn nhất trong các số tìm được ở bước 1.
Lời giải chi tiết:
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.\)
Ta có F(1,6;0,2)=250.1,6+160.0,2=432.
F(1,6;1,1)=250.1,6+160.1,1=576
F(0,3;1,1)=251
F(0,6;0,7)=262
Giá trị nhỏ nhất là F(0,3;1,1)=251.
Vậy để chi phí ít nhất thì cần mua 0,3kg thịt bò và 1,1 thịt lợn.
Bài 2.6 trang 30 SGK Toán 10 tập 1 – Kết nối tri thức thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài 2.6 thường bao gồm các dạng bài tập sau:
Để giải bài 2.6 trang 30 SGK Toán 10 tập 1 – Kết nối tri thức một cách hiệu quả, bạn cần thực hiện theo các bước sau:
Bài toán: Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ AM theo vectơ AB và AC.
Lời giải:
Ta có: AM = AB + BM. Vì M là trung điểm của BC nên BM = 1/2 BC. Do đó, AM = AB + 1/2 BC. Mà BC = AC - AB. Vậy, AM = AB + 1/2(AC - AB) = AB + 1/2 AC - 1/2 AB = 1/2 AB + 1/2 AC.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, bạn có thể tham khảo các bài tập tương tự sau:
Khi giải bài tập về vectơ, bạn cần lưu ý những điều sau:
Bài 2.6 trang 30 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp bạn củng cố kiến thức về vectơ và rèn luyện kỹ năng giải bài toán hình học. Hy vọng rằng với hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.