Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 55 và 56 sách giáo khoa Toán 10 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
1a và a có bằng nhau hay không? Trên một trục số, gọi O, A, M, N tương ứng biểu thị các số 0, 1, . Hãy nêu mối quan hệ về hướng và độ dài -a và -1a có mối quan hệ gì? Cho đường thẳng d đi qua hai điểm phân biệt A và B. Những khẳng định nào sau đây là đúng?
\(1\;\overrightarrow a \) và \(\overrightarrow a \) có bằng nhau hay không?
Phương pháp giải:
Hai vecto bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Ta có: Vecto \(1\;\overrightarrow a \) cùng hướng với vecto \(\overrightarrow a \) và \(\left| {1\;\overrightarrow a } \right| = \left| {\overrightarrow a } \right|\).
Vậy hai vecto \(1\;\overrightarrow a \) và \(\overrightarrow a \) bằng nhau.
\( - \;\overrightarrow a \) và \( - 1\;\overrightarrow a \) có mối quan hệ gì?
Phương pháp giải:
Vecto \(k\;\overrightarrow a \) (với \(k < 0,\;\overrightarrow a \ne \overrightarrow 0 \)) là vecto ngược hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(\left| k \right|\;\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
Ta có:
Vecto \( - \;\overrightarrow a \) là vecto đối của vecto \(\overrightarrow a \)
\( \Rightarrow - \;\overrightarrow a \) ngược hướng với vecto \(\overrightarrow a \) và \(\left| { - \;\overrightarrow a \;} \right| = \left| {\;\overrightarrow a \;} \right|\)
Lại có:
Vecto \( - 1\;\overrightarrow a \) là vecto ngược hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(\left| { - 1} \right|\;\left| {\overrightarrow a } \right| = \left| {\overrightarrow a } \right|\).
\( \Rightarrow - \;\overrightarrow a \) và \( - 1\;\overrightarrow a \) cùng hướng và có độ dài bằng nhau (bằng vecto\(\;\overrightarrow a \)).
Hay \( - \;\overrightarrow a = - 1\;\overrightarrow a \)
Cho vecto \(\overrightarrow {AB} = \overrightarrow a \). Hãy xác định điểm C sao cho \(\overrightarrow {BC} = \overrightarrow a \)
a) Tìm mối quan hệ giữa \(\overrightarrow {AB} \) và \(\overrightarrow a + \overrightarrow a \)
b) Vecto \(\overrightarrow a + \overrightarrow a \) có mối quan hệ như thế nào về hướng và độ dài đối với vecto \(\overrightarrow a \)
Phương pháp giải:
Hai vecto bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Xác định điểm C:
Trên tia AB lấy điểm C sao cho BC = a và B nằm giữa A, C.
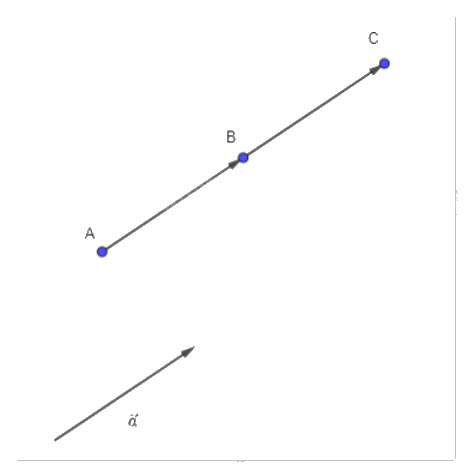
a) Vì \(\overrightarrow {AB} = \overrightarrow a = \overrightarrow {BC} \) nên A, B, C thẳng hàng và B là trung điểm của AC.
Vậy \(\overrightarrow a + \overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng, \(\left| {\overrightarrow a + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AB} } \right|\)
b) Ta có: \(\overrightarrow a + \overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng, \(\left| {\overrightarrow a + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AB} } \right|\)
Mà \(\overrightarrow {AB} = \overrightarrow a \) nên: \(\overrightarrow a + \overrightarrow a \) và \(\overrightarrow a \) cùng hướng, \(\left| {\overrightarrow a + \overrightarrow a } \right| = 2.\left| {\overrightarrow a } \right|\).
Trên một trục số, gọi O, A, M, N tương ứng biểu thị các số \(0;\;1;\;\sqrt 2 ;\; - \sqrt 2 \). Hãy nêu mối quan hệ về hướng và độ dài của mỗi vecto \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) với vecto \(\overrightarrow a = \overrightarrow {OA} \). Viết đẳng thức thể hiện mối quan hệ giữa hai vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \).
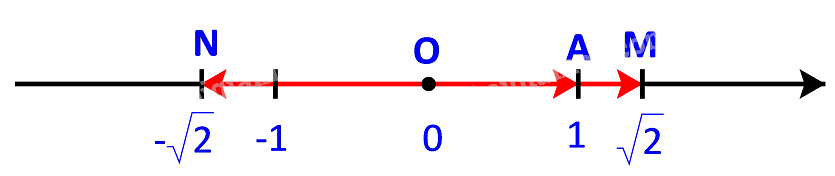
Phương pháp giải:
Vecto \(k\;\overrightarrow a \) (với \(k > 0,\;\overrightarrow a \ne \overrightarrow 0 \)) là vecto cùng hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(k\;\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
Dễ thấy:
Vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \) có cùng giá nên chúng cùng phương.
Mà vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \) cùng nằm trên tia OM nên chúng cùng chiều.
Vậy vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \) cùng hướng.
Ngoài ra, \(\left| {\overrightarrow {OM} } \right| = OM = \sqrt 2 \) và \(\left| {\overrightarrow {OA} } \right| = OA = 1\)
\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt 2 .\left| {\overrightarrow {OA} } \right|\)
Ta kết luận \(\overrightarrow {OM} = \sqrt 2 .\overrightarrow {OA} \).
Dễ thấy:
Vecto \(\overrightarrow {ON} \) và \(\overrightarrow {OA} \) có cùng giá nên chúng cùng phương.
Mà vecto \(\overrightarrow {ON} \) và \(\overrightarrow {OA} \) thuộc hai tia đối nhau nên chúng ngược chiều.
Vậy vecto \(\overrightarrow {ON} \) và \(\overrightarrow {OA} \) ngược hướng.
Ngoài ra, \(\left| {\overrightarrow {ON} } \right| = ON = \sqrt 2 \) và \(\left| {\overrightarrow {OA} } \right| = OA = 1\)
\( \Rightarrow \left| {\overrightarrow {ON} } \right| = \sqrt 2 .\left| {\overrightarrow {OA} } \right|\)
Ta kết luận \(\overrightarrow {ON} = -\sqrt 2 .\overrightarrow {OA} \).
Cho đường thẳng d đi qua hai điểm phân biệt A và B. Những khẳng định nào sau đây là đúng?
a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
b) Với điểm M bất kì, ta luôn có \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \)
c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số \(t \le 0\) để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
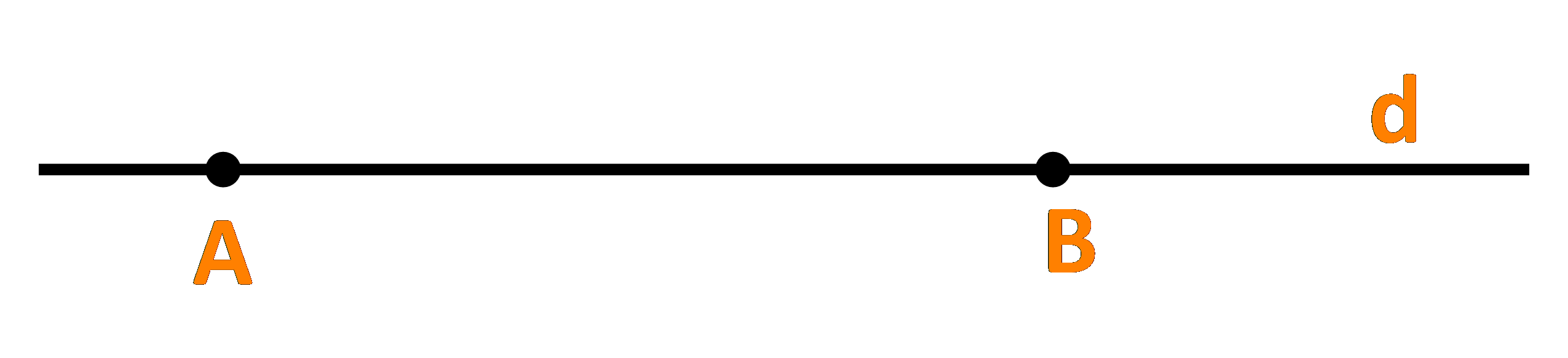
Phương pháp giải:
\(\overrightarrow a \) và \(\overrightarrow b \;\left( {\overrightarrow b \ne \overrightarrow 0 } \right)\) cùng phương khi và chỉ khi tồn tại số k để \(\overrightarrow a = k.\overrightarrow b \)
Nếu \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng thì \(k = \frac{{|\overrightarrow a |}}{{|\overrightarrow b |}}\)
Nếu \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng thì \(k = - \frac{{|\overrightarrow a |}}{{|\overrightarrow b |}}\)
Lời giải chi tiết:
a) Điểm M thuộc đường thẳng d khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng phương (cùng giá d)
Khi và chỉ khi tồn tại số t để \(\overrightarrow {AM} = t.\overrightarrow {AB} \).
Vậy khẳng định a) đúng.
b) Với điểm M bất kì, ta luôn có \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \)
Sai vì \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \) khi và chỉ khi \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng hướng.
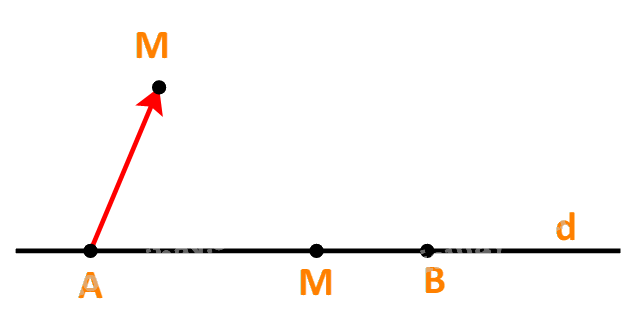
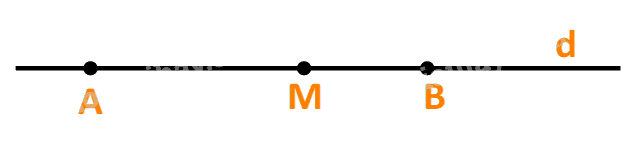
c) Điểm M thuộc tia đối của tia AB, tức là A nằm giữa M và B.
Khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) ngược hướng khi và chỉ khi tồn tại số \(t < 0\) để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
Vậy khẳng định c) sai.

Cho vecto \(\overrightarrow {AB} = \overrightarrow a \). Hãy xác định điểm C sao cho \(\overrightarrow {BC} = \overrightarrow a \)
a) Tìm mối quan hệ giữa \(\overrightarrow {AB} \) và \(\overrightarrow a + \overrightarrow a \)
b) Vecto \(\overrightarrow a + \overrightarrow a \) có mối quan hệ như thế nào về hướng và độ dài đối với vecto \(\overrightarrow a \)
Phương pháp giải:
Hai vecto bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Xác định điểm C:
Trên tia AB lấy điểm C sao cho BC = a và B nằm giữa A, C.
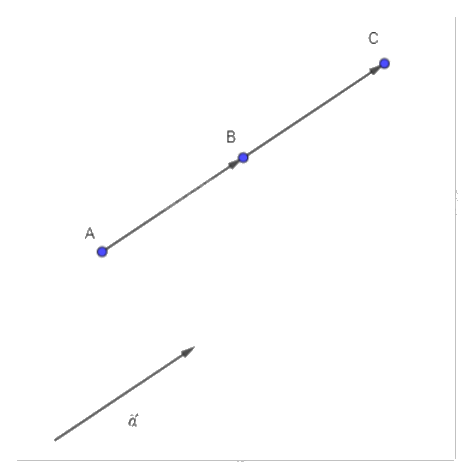
a) Vì \(\overrightarrow {AB} = \overrightarrow a = \overrightarrow {BC} \) nên A, B, C thẳng hàng và B là trung điểm của AC.
Vậy \(\overrightarrow a + \overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng, \(\left| {\overrightarrow a + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AB} } \right|\)
b) Ta có: \(\overrightarrow a + \overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng, \(\left| {\overrightarrow a + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AB} } \right|\)
Mà \(\overrightarrow {AB} = \overrightarrow a \) nên: \(\overrightarrow a + \overrightarrow a \) và \(\overrightarrow a \) cùng hướng, \(\left| {\overrightarrow a + \overrightarrow a } \right| = 2.\left| {\overrightarrow a } \right|\).
\(1\;\overrightarrow a \) và \(\overrightarrow a \) có bằng nhau hay không?
Phương pháp giải:
Hai vecto bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Ta có: Vecto \(1\;\overrightarrow a \) cùng hướng với vecto \(\overrightarrow a \) và \(\left| {1\;\overrightarrow a } \right| = \left| {\overrightarrow a } \right|\).
Vậy hai vecto \(1\;\overrightarrow a \) và \(\overrightarrow a \) bằng nhau.
Trên một trục số, gọi O, A, M, N tương ứng biểu thị các số \(0;\;1;\;\sqrt 2 ;\; - \sqrt 2 \). Hãy nêu mối quan hệ về hướng và độ dài của mỗi vecto \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) với vecto \(\overrightarrow a = \overrightarrow {OA} \). Viết đẳng thức thể hiện mối quan hệ giữa hai vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \).
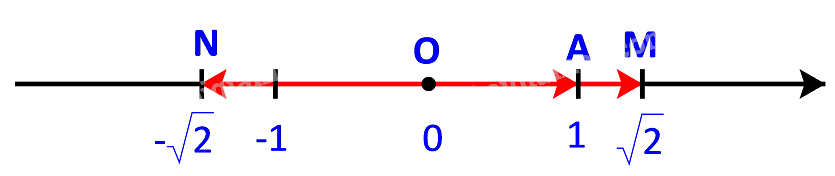
Phương pháp giải:
Vecto \(k\;\overrightarrow a \) (với \(k > 0,\;\overrightarrow a \ne \overrightarrow 0 \)) là vecto cùng hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(k\;\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
Dễ thấy:
Vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \) có cùng giá nên chúng cùng phương.
Mà vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \) cùng nằm trên tia OM nên chúng cùng chiều.
Vậy vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \) cùng hướng.
Ngoài ra, \(\left| {\overrightarrow {OM} } \right| = OM = \sqrt 2 \) và \(\left| {\overrightarrow {OA} } \right| = OA = 1\)
\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt 2 .\left| {\overrightarrow {OA} } \right|\)
Ta kết luận \(\overrightarrow {OM} = \sqrt 2 .\overrightarrow {OA} \).
Dễ thấy:
Vecto \(\overrightarrow {ON} \) và \(\overrightarrow {OA} \) có cùng giá nên chúng cùng phương.
Mà vecto \(\overrightarrow {ON} \) và \(\overrightarrow {OA} \) thuộc hai tia đối nhau nên chúng ngược chiều.
Vậy vecto \(\overrightarrow {ON} \) và \(\overrightarrow {OA} \) ngược hướng.
Ngoài ra, \(\left| {\overrightarrow {ON} } \right| = ON = \sqrt 2 \) và \(\left| {\overrightarrow {OA} } \right| = OA = 1\)
\( \Rightarrow \left| {\overrightarrow {ON} } \right| = \sqrt 2 .\left| {\overrightarrow {OA} } \right|\)
Ta kết luận \(\overrightarrow {ON} = -\sqrt 2 .\overrightarrow {OA} \).
\( - \;\overrightarrow a \) và \( - 1\;\overrightarrow a \) có mối quan hệ gì?
Phương pháp giải:
Vecto \(k\;\overrightarrow a \) (với \(k < 0,\;\overrightarrow a \ne \overrightarrow 0 \)) là vecto ngược hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(\left| k \right|\;\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
Ta có:
Vecto \( - \;\overrightarrow a \) là vecto đối của vecto \(\overrightarrow a \)
\( \Rightarrow - \;\overrightarrow a \) ngược hướng với vecto \(\overrightarrow a \) và \(\left| { - \;\overrightarrow a \;} \right| = \left| {\;\overrightarrow a \;} \right|\)
Lại có:
Vecto \( - 1\;\overrightarrow a \) là vecto ngược hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(\left| { - 1} \right|\;\left| {\overrightarrow a } \right| = \left| {\overrightarrow a } \right|\).
\( \Rightarrow - \;\overrightarrow a \) và \( - 1\;\overrightarrow a \) cùng hướng và có độ dài bằng nhau (bằng vecto\(\;\overrightarrow a \)).
Hay \( - \;\overrightarrow a = - 1\;\overrightarrow a \)
Cho đường thẳng d đi qua hai điểm phân biệt A và B. Những khẳng định nào sau đây là đúng?
a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
b) Với điểm M bất kì, ta luôn có \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \)
c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số \(t \le 0\) để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
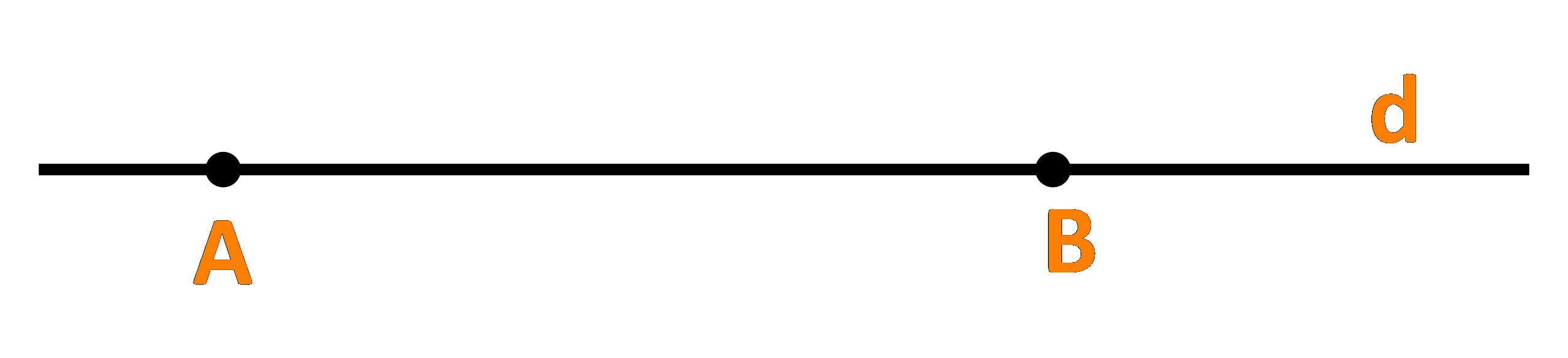
Phương pháp giải:
\(\overrightarrow a \) và \(\overrightarrow b \;\left( {\overrightarrow b \ne \overrightarrow 0 } \right)\) cùng phương khi và chỉ khi tồn tại số k để \(\overrightarrow a = k.\overrightarrow b \)
Nếu \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng thì \(k = \frac{{|\overrightarrow a |}}{{|\overrightarrow b |}}\)
Nếu \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng thì \(k = - \frac{{|\overrightarrow a |}}{{|\overrightarrow b |}}\)
Lời giải chi tiết:
a) Điểm M thuộc đường thẳng d khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng phương (cùng giá d)
Khi và chỉ khi tồn tại số t để \(\overrightarrow {AM} = t.\overrightarrow {AB} \).
Vậy khẳng định a) đúng.
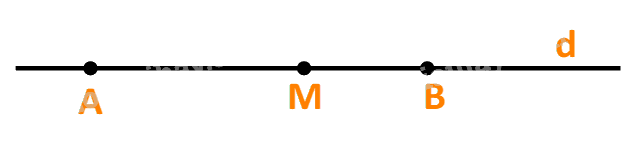
b) Với điểm M bất kì, ta luôn có \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \)
Sai vì \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \) khi và chỉ khi \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng hướng.
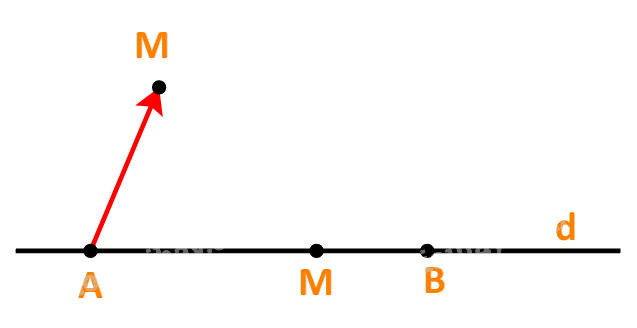
c) Điểm M thuộc tia đối của tia AB, tức là A nằm giữa M và B.
Khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) ngược hướng khi và chỉ khi tồn tại số \(t < 0\) để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
Vậy khẳng định c) sai.

Mục 1 của chương trình Toán 10 tập 1 Kết nối tri thức tập trung vào việc ôn tập và mở rộng kiến thức về tập hợp. Các bài tập trang 55 và 56 SGK Toán 10 tập 1 yêu cầu học sinh vận dụng các khái niệm về tập hợp, các phép toán trên tập hợp (hợp, giao, hiệu, bù) và các tính chất của chúng để giải quyết các bài toán cụ thể.
Bài 1.19 yêu cầu học sinh xác định các tập hợp con, tập hợp bằng nhau và sử dụng các ký hiệu tập hợp để biểu diễn các mối quan hệ giữa các tập hợp. Để giải bài này, học sinh cần nắm vững định nghĩa về tập hợp con, tập hợp bằng nhau và hiểu rõ cách sử dụng các ký hiệu tập hợp.
Ví dụ:
Bài 1.20 yêu cầu học sinh thực hiện các phép toán trên tập hợp, bao gồm hợp, giao, hiệu và bù. Để giải bài này, học sinh cần hiểu rõ định nghĩa của từng phép toán và biết cách áp dụng chúng vào các bài toán cụ thể.
Ví dụ:
Cho A = {1, 2, 3} và B = {2, 4, 5}. Khi đó:
Bài 1.21 thường liên quan đến việc chứng minh các đẳng thức tập hợp. Để giải bài này, học sinh cần sử dụng các tính chất của các phép toán trên tập hợp và áp dụng các quy tắc logic để chứng minh đẳng thức.
Ví dụ:
Chứng minh A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Để chứng minh đẳng thức này, ta có thể sử dụng phương pháp chứng minh bằng tập hợp, tức là chứng minh rằng mọi phần tử thuộc vế trái đều thuộc vế phải và ngược lại.
Giaitoan.edu.vn cung cấp lời giải chi tiết và đáp án cho tất cả các bài tập trong mục 1 trang 55, 56 SGK Toán 10 tập 1 Kết nối tri thức. Các lời giải được trình bày một cách rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin hơn trong học tập.
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết cho các môn Toán từ lớp 6 đến lớp 12. Chúng tôi cam kết mang đến cho học sinh một trải nghiệm học tập hiệu quả và thú vị.
Hy vọng rằng với những hướng dẫn và lời giải chi tiết trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 1 trang 55, 56 SGK Toán 10 tập 1 Kết nối tri thức. Chúc các em học tập tốt!