Bài 1.15 trang 19 SGK Toán 10 tập 1 thuộc chương 1: Mệnh đề và tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về tập hợp, các phép toán trên tập hợp để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
Đề bài
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( - 4;1] \cap [0;3)\)
b) \((0;2] \cup (- 3;1]\)
c) \(( - 2;1] \cap (1;+ \infty )\)
d) \(\mathbb{R}{\rm{\backslash }}( - \infty ;3]\)
Phương pháp giải - Xem chi tiết
Biểu diễn các tập hợp trên trục số
Lời giải chi tiết
a) Ta có:
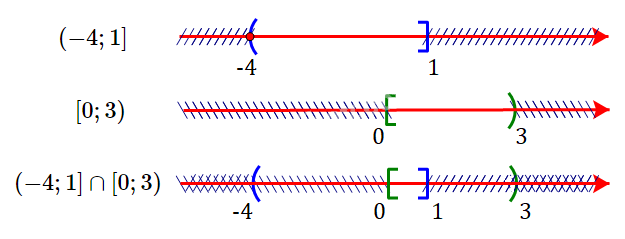
Giao của hai tập hợp là \(( - 4;1] \cap [0;3) = \left[ {0;1} \right]\)
b) Ta có:
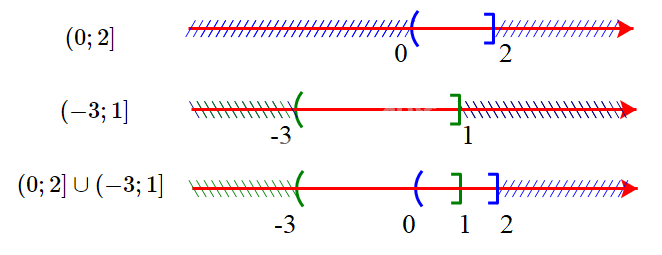
Hợp của hai tập hợp là \((0;2] \cup ( - 3;1] = ( - 3;2]\)
c) Ta có:
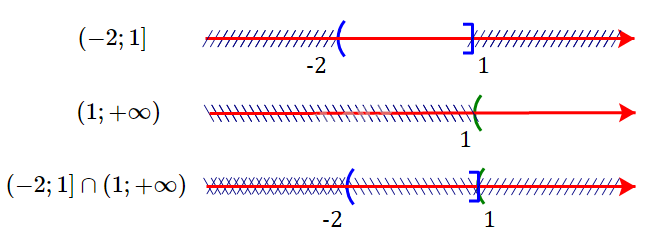
Giao của hai tập hợp là \(( - 2;1] \cap (1;+ \infty )= \emptyset\)
d) Ta có:
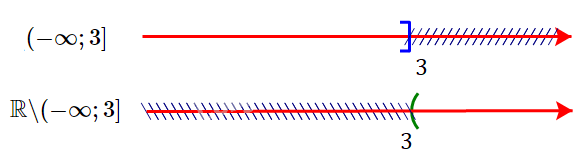
Phần bù của tập hợp \(( - \infty ;3]\) trong \(\mathbb{R}\) là \(\mathbb{R}{\rm{\backslash }}( - \infty ;3] = (3; + \infty )\)
Cho các tập hợp: A = {0; 1; 2; 3; 4; 5}; B = {2; 3; 4; 5; 6}; C = {1; 3; 5; 7; 9}. Tìm:
Để giải bài 1.15 trang 19 SGK Toán 10 tập 1 – Kết nối tri thức, chúng ta cần nắm vững các khái niệm và quy tắc về các phép toán trên tập hợp:
A ∪ B = {0; 1; 2; 3; 4; 5; 6}. Tập hợp này chứa tất cả các phần tử có mặt trong A hoặc B.
A ∩ B = {2; 3; 4; 5}. Tập hợp này chỉ chứa các phần tử chung của A và B.
A \ B = {0; 1}. Tập hợp này chứa các phần tử thuộc A nhưng không thuộc B.
B \ A = {6}. Tập hợp này chứa các phần tử thuộc B nhưng không thuộc A.
Bài tập này là một ví dụ điển hình về việc áp dụng các phép toán trên tập hợp. Việc hiểu rõ các phép toán này là rất quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 10.
Để nắm vững kiến thức về tập hợp, bạn nên:
Cho A = {1; 2; 3} và B = {3; 4; 5}. Hãy tìm A ∪ B, A ∩ B, A \ B, B \ A.
Lời giải:
Bài 1.15 trang 19 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập cơ bản về tập hợp. Việc giải bài tập này giúp học sinh củng cố kiến thức về các phép toán trên tập hợp và rèn luyện kỹ năng giải toán. Giaitoan.edu.vn hy vọng với lời giải chi tiết và các ví dụ minh họa, các bạn học sinh sẽ hiểu rõ hơn về bài tập này và tự tin hơn trong quá trình học tập.