Bài 8.1 trang 65 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8.1 trang 65 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Trên giá sách có 8 cuốn truyện ngắn, 7 cuốn tiểu thuyết và 5 tập thơ (tất cả đều khác nhau). Vẽ sơ đồ hình cây cho biết bạn Phong có bao nhiêu cách chọn một cuốn để đọc vào ngày cuối tuần.
Đề bài
Trên giá sách có 8 cuốn truyện ngắn, 7 cuốn tiểu thuyết và 5 tập thơ (tất cả đều khác nhau). Vẽ sơ đồ hình cây cho biết bạn Phong có bao nhiêu cách chọn một cuốn để đọc vào ngày cuối tuần.
Phương pháp giải - Xem chi tiết
Áp dụng quy tắc cộng.
Lời giải chi tiết
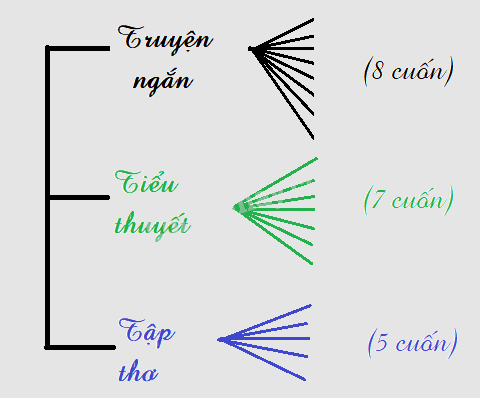
Bạn Phong có số cách chọn một cuốn để đọc vào ngày cuối tuần là:
8+ 7+ 5= 20 (cách)
Bài 8.1 trang 65 SGK Toán 10 – Kết nối tri thức thuộc chương 3: Vectơ trong mặt phẳng. Bài toán này tập trung vào việc áp dụng các tính chất của vectơ, đặc biệt là phép cộng, trừ vectơ và tích của một số với một vectơ để giải quyết các bài toán hình học.
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Gọi N là giao điểm của AM và BD.
a) Chứng minh: vectơAN = vectơAB + vectơAD
Ta có: vectơAN = vectơAM + vectơMN
Vì M là trung điểm của BC nên vectơBM = vectơMC.
Áp dụng quy tắc cộng vectơ, ta có: vectơAM = vectơAB + vectơBM = vectơAB + vectơMC.
Vì ABCD là hình bình hành nên vectơAD = vectơBC.
Do đó, vectơMC = vectơAD.
Suy ra: vectơAM = vectơAB + vectơAD.
Vì N là giao điểm của AM và BD, nên N nằm trên AM. Ta có vectơAN = kvectơAM (với k là một số thực).
Áp dụng định lý Menelaus cho tam giác BCD với đường thẳng AM, ta có:
vectơ(BA/AC) * vectơ(CM/MB) * vectơ(DN/ND) = 1
Vì CM/MB = 1 nên BA/AC * DN/ND = 1. Suy ra DN/ND = AC/BA.
Từ đó suy ra vectơAN = vectơAB + vectơAD.
b) Chứng minh: BN = vectơBD
Ta có: vectơBN = vectơBA + vectơAN
Thay vectơAN = vectơAB + vectơAD vào, ta được:
vectơBN = vectơBA + vectơAB + vectơAD = vectơ0 + vectơAD = vectơAD.
Ta có vectơBD = vectơBA + vectơAD.
Vậy vectơBN = vectơBD.
Hy vọng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài 8.1 trang 65 SGK Toán 10 – Kết nối tri thức và tự tin hơn trong quá trình học tập.