Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 2 trang 84, 85 SGK Toán 10 tập 2 - Kết nối tri thức. Bài viết này cung cấp đáp án đầy đủ, dễ hiểu, cùng với các bước giải thích rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng tham khảo!
Trong một cuộc tổng điều tra dân số, điều tra viên chọn ngẫu nhiên một gia đình có ba người con và quan tâm giới tính của ba người con này.
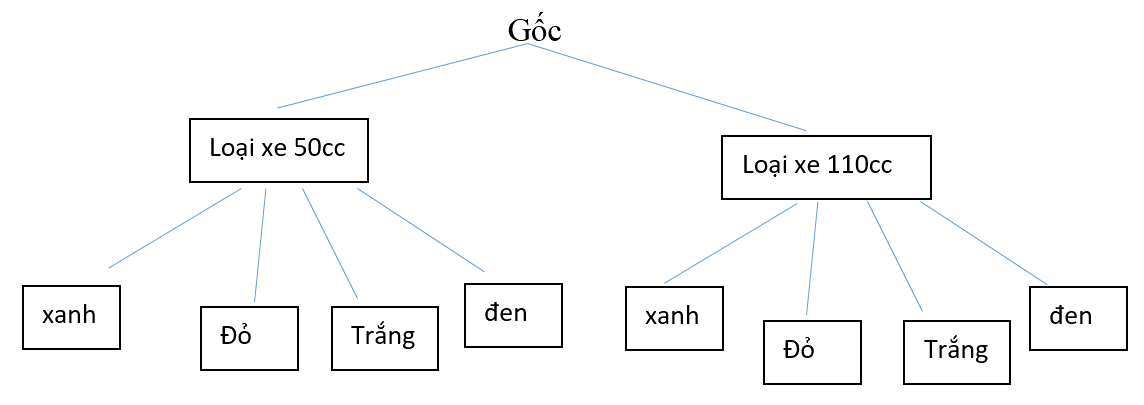
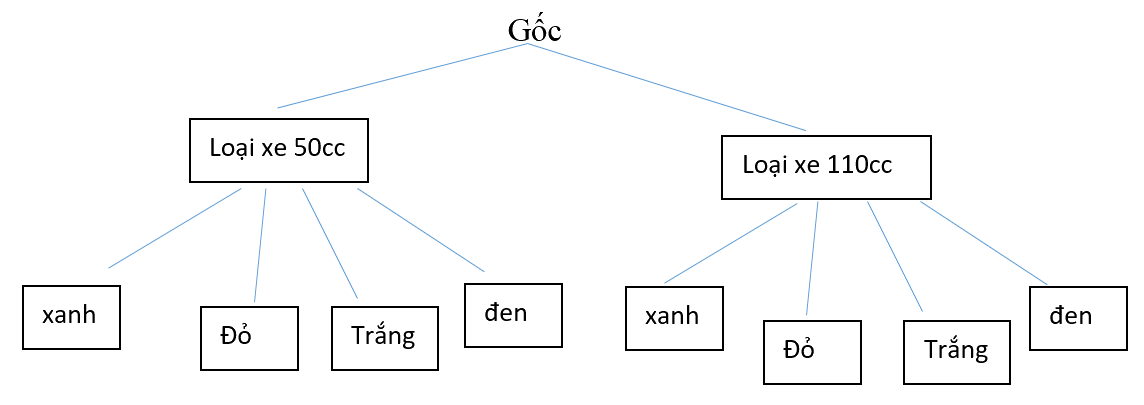
Trở lại trò chơi “Vòng quay may mắn” ở HĐ2. Tính xác suất để người chơi nhận: được loại xe 110 cc có màu trắng hoặc màu xanh.
Lời giải chi tiết:
Dựa vào sơ đồ cây, ta thấy \(n\left( \Omega \right) = 8\).
Gọi E là biến cố “Người chơi nhận được loại xe 110 cc có màu trắng hoặc màu xanh”.
Ta có \(n\left( E \right) = 2\). Vậy \(P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega \right)}} = 0,25\).
Trong trò chơi "Vòng quay may mắn", người chơi sẽ quay hai bánh xe. Mũi tên ở bánh xe thứ nhất có thể dừng ở một trong hai vị trí: Loại xe 50 CC và Loại xe 110 cc. Mũi tên ở bánh xe thứ hai có thể dừng ở một trong bốn vị trí: màu đen, màu trắng, màu đỏ và màu xanh. Vị trí của mũi tên trên hai bánh xe sẽ xác định người chơi nhận được loại xe nào, màu gì. Phép thử T là quay hai bánh xe. Hãy vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
Lời giải chi tiết:
b) Gọi E là biến cố: “Gia đình đó có một người con trai và hai con gái”.
Dựa vào sơ đồ cây, ta có \(n\left( \Omega \right) = 8\) và \(n\left( E \right) = 3\). Vậy \(P\left( E \right) = \frac{3}{8}\).
Trong một cuộc tổng điều tra dân số, điều tra viên chọn ngẫu nhiên một gia đình có ba người con và quan tâm giới tính của ba người con này.
a) Vẽ sơ đồ hình cây để mô tả các phần tử của không gian mẫu.
b) Giả thiết rằng khả năng sinh con trai và khả năng sinh con gái là như nhau. Tính xác suất để gia đình đó có một con trai và hai con gái.
Lời giải chi tiết:
a, Sơ đồ tư duy:
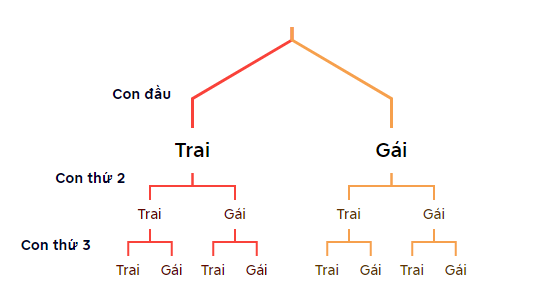
Kí hiệu con trai: T, con gái: G.
Các kết quả có thể xảy ra là: GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT.
Do đó: \(\Omega\)= {GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT}.
Vậy n(Ω) = 8.
b) Gọi biến cố A: “Gia đình đó có một con trai và hai con gái”.
Ta có: A = {GTG; TGG; GGT}. Do đó, \(n(A)\)= 3.
Vậy \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{3}{8}\)
Trong trò chơi "Vòng quay may mắn", người chơi sẽ quay hai bánh xe. Mũi tên ở bánh xe thứ nhất có thể dừng ở một trong hai vị trí: Loại xe 50 CC và Loại xe 110 cc. Mũi tên ở bánh xe thứ hai có thể dừng ở một trong bốn vị trí: màu đen, màu trắng, màu đỏ và màu xanh. Vị trí của mũi tên trên hai bánh xe sẽ xác định người chơi nhận được loại xe nào, màu gì. Phép thử T là quay hai bánh xe. Hãy vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
Lời giải chi tiết:
b) Gọi E là biến cố: “Gia đình đó có một người con trai và hai con gái”.
Dựa vào sơ đồ cây, ta có \(n\left( \Omega \right) = 8\) và \(n\left( E \right) = 3\). Vậy \(P\left( E \right) = \frac{3}{8}\).
Trở lại trò chơi “Vòng quay may mắn” ở HĐ2. Tính xác suất để người chơi nhận: được loại xe 110 cc có màu trắng hoặc màu xanh.
Lời giải chi tiết:
Dựa vào sơ đồ cây, ta thấy \(n\left( \Omega \right) = 8\).
Gọi E là biến cố “Người chơi nhận được loại xe 110 cc có màu trắng hoặc màu xanh”.
Ta có \(n\left( E \right) = 2\). Vậy \(P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega \right)}} = 0,25\).
Trong một cuộc tổng điều tra dân số, điều tra viên chọn ngẫu nhiên một gia đình có ba người con và quan tâm giới tính của ba người con này.
a) Vẽ sơ đồ hình cây để mô tả các phần tử của không gian mẫu.
b) Giả thiết rằng khả năng sinh con trai và khả năng sinh con gái là như nhau. Tính xác suất để gia đình đó có một con trai và hai con gái.
Lời giải chi tiết:
a, Sơ đồ tư duy:
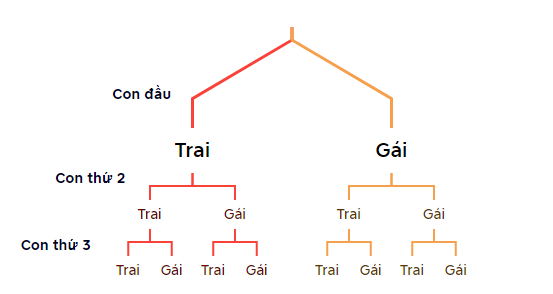
Kí hiệu con trai: T, con gái: G.
Các kết quả có thể xảy ra là: GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT.
Do đó: \(\Omega\)= {GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT}.
Vậy n(Ω) = 8.
b) Gọi biến cố A: “Gia đình đó có một con trai và hai con gái”.
Ta có: A = {GTG; TGG; GGT}. Do đó, \(n(A)\)= 3.
Vậy \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{3}{8}\)
Mục 2 của chương trình Toán 10 tập 2 - Kết nối tri thức tập trung vào việc nghiên cứu về vectơ. Cụ thể, trang 84 và 85 của sách giáo khoa đi sâu vào các khái niệm như tích vô hướng của hai vectơ, ứng dụng của tích vô hướng trong việc tính góc giữa hai vectơ, và xác định tính vuông góc của hai vectơ. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán hình học và vật lý ở các lớp trên.
Mục 2 bao gồm một loạt các bài tập được thiết kế để giúp học sinh hiểu rõ và vận dụng các kiến thức đã học. Các bài tập này thường yêu cầu học sinh:
Bài tập này yêu cầu học sinh áp dụng công thức tính tích vô hướng của hai vectơ: a.b = |a||b|cos(θ), trong đó θ là góc giữa hai vectơ a và b. Để giải bài tập này, học sinh cần xác định tọa độ của hai vectơ và góc giữa chúng. Nếu góc không được cho trước, học sinh có thể sử dụng các công thức hình học để tính góc.
Để tính góc giữa hai vectơ, học sinh có thể sử dụng công thức sau: cos(θ) = (a.b) / (|a||b|). Sau khi tính được cos(θ), học sinh có thể sử dụng máy tính hoặc bảng lượng giác để tìm ra giá trị của θ.
Hai vectơ a và b được gọi là vuông góc nếu tích vô hướng của chúng bằng 0: a.b = 0. Bài tập này yêu cầu học sinh tính tích vô hướng của hai vectơ và kết luận xem chúng có vuông góc hay không.
Tích vô hướng có nhiều ứng dụng quan trọng trong hình học, chẳng hạn như:
Ví dụ 1: Cho hai vectơ a = (2, 3) và b = (-1, 4). Tính tích vô hướng của a và b.
Giải: a.b = (2)(-1) + (3)(4) = -2 + 12 = 10
Ví dụ 2: Cho hai vectơ a = (1, 0) và b = (0, 1). Tính góc giữa a và b.
Giải: a.b = (1)(0) + (0)(1) = 0. Vì a.b = 0, nên hai vectơ a và b vuông góc với nhau. Góc giữa chúng là 90 độ.
Việc giải các bài tập trong mục 2 trang 84, 85 SGK Toán 10 tập 2 - Kết nối tri thức đòi hỏi học sinh phải nắm vững các khái niệm và công thức liên quan đến vectơ và tích vô hướng. Bằng cách luyện tập thường xuyên và áp dụng các kiến thức đã học vào thực tế, học sinh có thể nâng cao kỹ năng giải toán và đạt kết quả tốt trong môn Toán.
| Công thức | Mô tả |
|---|---|
| a.b = |a||b|cos(θ) | Tích vô hướng của hai vectơ |
| cos(θ) = (a.b) / (|a||b|) | Tính góc giữa hai vectơ |
| a.b = 0 | Điều kiện để hai vectơ vuông góc |