Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 Kết nối tri thức tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 1 của chương trình Toán 10 tập 1 tập trung vào những khái niệm cơ bản về tập hợp, số thực và các phép toán trên số thực. Việc hiểu rõ những kiến thức này là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.
Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt OA=i (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số -3/2. Hãy biểu thị mỗi vectơ OM, ON theo vectơ i Trong Hình 4.33: a) Hãy biểu thị mỗi vectơ OM, ON theo các vectơ i, j. Tìm tọa độ của vecto 0
Tìm tọa độ của \(\overrightarrow 0 \)
Lời giải chi tiết:
Vì: \(\overrightarrow 0 = 0.\;\overrightarrow i + 0.\;\overrightarrow j \) nên \(\overrightarrow 0 \) có tọa độ là (0;0).
Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt \(\overrightarrow {OA} = \overrightarrow i \) (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số \( - \frac{3}{2}\). Hãy biểu thị mỗi vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) theo vectơ \(\overrightarrow i \).
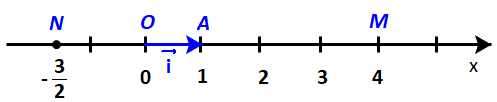
Phương pháp giải:
+) \(\overrightarrow a = k.\overrightarrow b ,\quad (k > 0) \Leftrightarrow \) Vecto \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng, \(\left| {\overrightarrow a } \right| = k.\left| {\overrightarrow b } \right|\quad (k > 0)\)
+) \(\overrightarrow a = k.\overrightarrow b ,\quad (k < 0) \Leftrightarrow \) Vecto \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng, \(\left| {\overrightarrow a } \right| = - k.\left| {\overrightarrow b } \right|\quad (k < 0)\)
(\(\overrightarrow b \ne \overrightarrow 0 \))
Lời giải chi tiết:
Dễ thấy:
vectơ \(\overrightarrow {OM} \) cùng hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {OM} } \right| = 4 = 4\left| {\overrightarrow i } \right|\)
Do đó: \(\overrightarrow {OM} = 4\,.\,\overrightarrow i \)
Tương tự, vectơ \(\overrightarrow {ON} \) ngược hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {ON} } \right| = \frac{3}{2} = \frac{3}{2}\left| {\overrightarrow i } \right|\)
Do đó: \(\overrightarrow {ON} = - \frac{3}{2}\,.\,\overrightarrow i \)
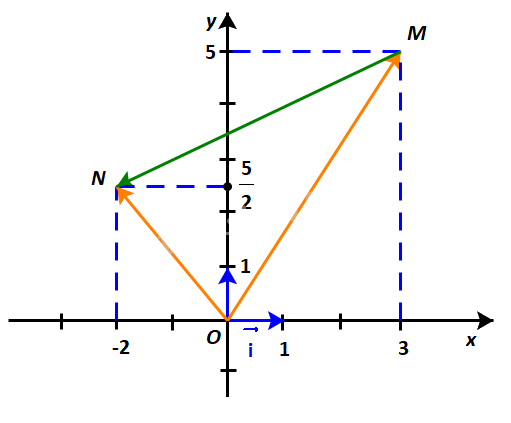
Trong Hình 4.33:
a) Hãy biểu thị mỗi vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
b) Hãy biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) từ đó biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
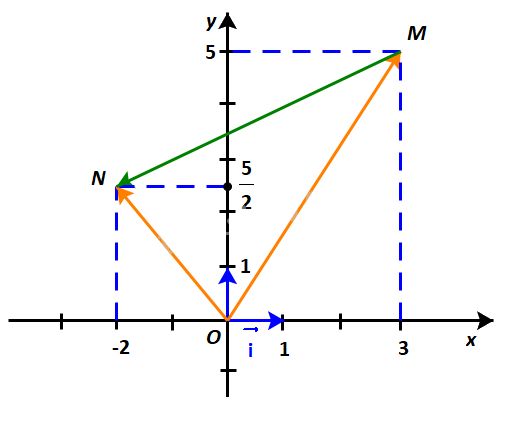
Phương pháp giải:
a) Quy tắc hình bình hành:
Tứ giác OAMB là hình bình hành thì \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \)
b) Quy tắc hiệu: \(\overrightarrow {MN} = \overrightarrow {ON} - \;\overrightarrow {OM} \)
Lời giải chi tiết:
Dựng hình bình hành OAMB và OCND như hình dưới:
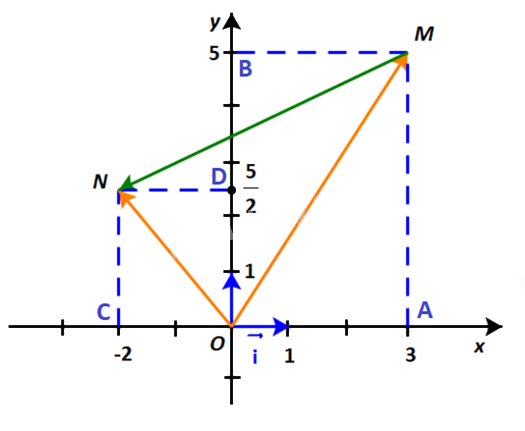
Khi đó: \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) và \(\overrightarrow {ON} = \overrightarrow {OC} + \overrightarrow {OD} \).
Dễ thấy:
\(\overrightarrow {OA} = 3\;\overrightarrow i ;\;\,\overrightarrow {OB} = 5\;\overrightarrow j \) và \(\overrightarrow {OC} = - 2\;\overrightarrow i ;\;\,\overrightarrow {OD} = \frac{5}{2}\;\overrightarrow j \)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {OM} = 3\;\overrightarrow i + 5\;\overrightarrow j \\\overrightarrow {ON} = - 2\;\overrightarrow i + \frac{5}{2}\;\overrightarrow j \end{array} \right.\)
b) Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} - \;\overrightarrow {OM} \) (quy tắc hiệu)
\(\begin{array}{l} \Rightarrow \overrightarrow {MN} = \left( { - 2\;\overrightarrow i + \frac{5}{2}\;\overrightarrow j } \right) - \left( {\;3\;\overrightarrow i + 5\;\overrightarrow j } \right)\\ \Leftrightarrow \overrightarrow {MN} = \left( { - 2\;\overrightarrow i - 3\;\overrightarrow i } \right) + \left( {\frac{5}{2}\;\overrightarrow j - 5\;\overrightarrow j } \right)\\ \Leftrightarrow \overrightarrow {MN} = - 5\;\overrightarrow i - \frac{5}{2}\;\overrightarrow j \end{array}\)
Vậy \(\overrightarrow {MN} = - 5\;\overrightarrow i - \frac{5}{2}\;\overrightarrow j \).
Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt \(\overrightarrow {OA} = \overrightarrow i \) (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số \( - \frac{3}{2}\). Hãy biểu thị mỗi vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) theo vectơ \(\overrightarrow i \).
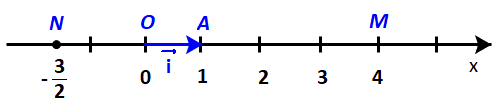
Phương pháp giải:
+) \(\overrightarrow a = k.\overrightarrow b ,\quad (k > 0) \Leftrightarrow \) Vecto \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng, \(\left| {\overrightarrow a } \right| = k.\left| {\overrightarrow b } \right|\quad (k > 0)\)
+) \(\overrightarrow a = k.\overrightarrow b ,\quad (k < 0) \Leftrightarrow \) Vecto \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng, \(\left| {\overrightarrow a } \right| = - k.\left| {\overrightarrow b } \right|\quad (k < 0)\)
(\(\overrightarrow b \ne \overrightarrow 0 \))
Lời giải chi tiết:
Dễ thấy:
vectơ \(\overrightarrow {OM} \) cùng hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {OM} } \right| = 4 = 4\left| {\overrightarrow i } \right|\)
Do đó: \(\overrightarrow {OM} = 4\,.\,\overrightarrow i \)
Tương tự, vectơ \(\overrightarrow {ON} \) ngược hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {ON} } \right| = \frac{3}{2} = \frac{3}{2}\left| {\overrightarrow i } \right|\)
Do đó: \(\overrightarrow {ON} = - \frac{3}{2}\,.\,\overrightarrow i \)
Trong Hình 4.33:
a) Hãy biểu thị mỗi vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
b) Hãy biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) từ đó biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
Phương pháp giải:
a) Quy tắc hình bình hành:
Tứ giác OAMB là hình bình hành thì \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \)
b) Quy tắc hiệu: \(\overrightarrow {MN} = \overrightarrow {ON} - \;\overrightarrow {OM} \)
Lời giải chi tiết:
Dựng hình bình hành OAMB và OCND như hình dưới:
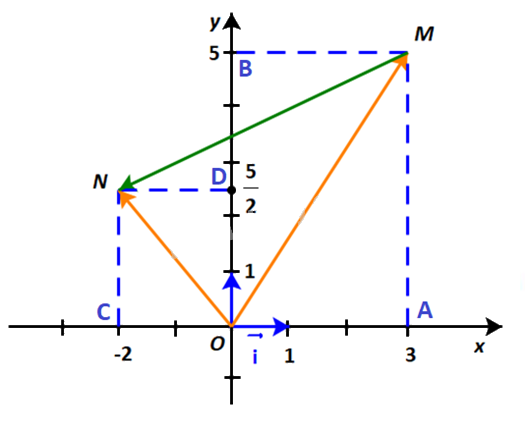
Khi đó: \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) và \(\overrightarrow {ON} = \overrightarrow {OC} + \overrightarrow {OD} \).
Dễ thấy:
\(\overrightarrow {OA} = 3\;\overrightarrow i ;\;\,\overrightarrow {OB} = 5\;\overrightarrow j \) và \(\overrightarrow {OC} = - 2\;\overrightarrow i ;\;\,\overrightarrow {OD} = \frac{5}{2}\;\overrightarrow j \)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {OM} = 3\;\overrightarrow i + 5\;\overrightarrow j \\\overrightarrow {ON} = - 2\;\overrightarrow i + \frac{5}{2}\;\overrightarrow j \end{array} \right.\)
b) Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} - \;\overrightarrow {OM} \) (quy tắc hiệu)
\(\begin{array}{l} \Rightarrow \overrightarrow {MN} = \left( { - 2\;\overrightarrow i + \frac{5}{2}\;\overrightarrow j } \right) - \left( {\;3\;\overrightarrow i + 5\;\overrightarrow j } \right)\\ \Leftrightarrow \overrightarrow {MN} = \left( { - 2\;\overrightarrow i - 3\;\overrightarrow i } \right) + \left( {\frac{5}{2}\;\overrightarrow j - 5\;\overrightarrow j } \right)\\ \Leftrightarrow \overrightarrow {MN} = - 5\;\overrightarrow i - \frac{5}{2}\;\overrightarrow j \end{array}\)
Vậy \(\overrightarrow {MN} = - 5\;\overrightarrow i - \frac{5}{2}\;\overrightarrow j \).
Tìm tọa độ của \(\overrightarrow 0 \)
Lời giải chi tiết:
Vì: \(\overrightarrow 0 = 0.\;\overrightarrow i + 0.\;\overrightarrow j \) nên \(\overrightarrow 0 \) có tọa độ là (0;0).
Mục 1 của SGK Toán 10 tập 1 Kết nối tri thức giới thiệu những khái niệm cơ bản về tập hợp, số thực và các phép toán trên số thực. Đây là nền tảng quan trọng cho việc học toán ở các lớp trên. Trang 60 và 61 tập trung vào các bài tập vận dụng các kiến thức đã học để giải quyết các vấn đề cụ thể.
Liệt kê các phần tử của mỗi tập hợp sau: A = {x | x là số tự nhiên nhỏ hơn 10}; B = {x | x là số chẵn nhỏ hơn 10}; C = {x | x là số nguyên tố nhỏ hơn 10}.
Lời giải:
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
(a) 3 ∈ N; (b) -3 ∉ N; (c) 2,5 ∈ Q; (d) -2,5 ∉ Q; (e) √2 ∈ R.
Lời giải:
Sắp xếp các số thực sau theo thứ tự tăng dần: -2; 0; 1,5; -3,2; 0,7; √2.
Lời giải:
-3,2 < -2 < 0 < 0,7 < √2 ≈ 1,414 < 1,5
Thực hiện các phép tính sau:
(a) 2,5 + (-3,7); (b) (-1,2) - 4,5; (c) (-2,3) * 1,5; (d) 6,8 : (-2).
Lời giải:
Để nắm vững kiến thức về tập hợp, số thực và các phép toán trên số thực, các em nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Việc giải nhiều bài tập sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 10. Hãy truy cập giaitoan.edu.vn để được hỗ trợ giải các bài tập khác và nâng cao kiến thức của mình.