Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 2 trang 36, 37 sách giáo khoa Toán 10 tập 1 chương trình Kết nối tri thức. Bài viết này cung cấp đáp án đầy đủ, chính xác, cùng với phương pháp giải rõ ràng, giúp học sinh dễ dàng nắm vững kiến thức và hoàn thành bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, cập nhật nhanh chóng và dễ tiếp cận, hỗ trợ tối đa cho quá trình học tập của bạn.
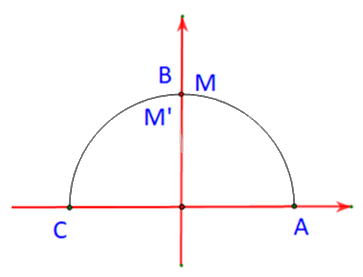
Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?
Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa \(\sin \alpha \) và \(\sin \left( {{{180}^o} - \alpha } \right)\), giữa \(\cos \alpha \) và \(\cos \left( {{{180}^o} - \alpha } \right)\).
Phương pháp giải:
Nhận xét vị trí của M và M’ trong mỗi trường hợp: \(\alpha = {90^o};\;\alpha < {90^o};\;\alpha > {90^o}.\)
Khi \({0^o} < \alpha < {90^o}\): \(\cos \alpha ,\;\sin \alpha \) tương ứng là hoành độ và tung độ của điểm M.
Lời giải chi tiết:
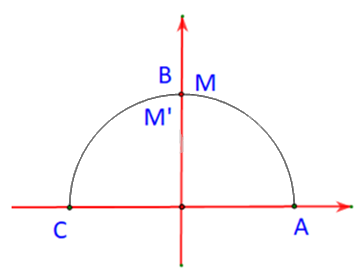
M, M’ là hai điểm trên nửa đường tròn đơn vị tương ứng với hai góc \(\alpha \) và \({180^o} - \alpha \).
Giả sử \(M\left( {{x_0};{y_o}} \right)\). Khi đó \(\cos \alpha = {x_0};\;\;\sin \alpha = {y_o}\)
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \(\alpha = {180^o} - \alpha = {90^o}\)
Tức là M và M’ lần lượt trùng nhau và trùng với B.
Và \(\left\{ \begin{array}{l}\cos \alpha = - \cos \left( {{{180}^o} - \alpha } \right) = 0;\\\sin \alpha = \sin \left( {{{180}^o} - \alpha } \right) = \sin {90^o} = 1.\\\cot \alpha = 0\end{array} \right.\)
Không tồn tại \(\tan \alpha \) với \(\alpha = {90^o}\)
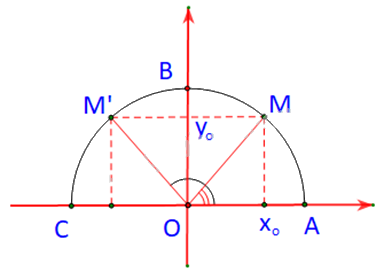
Trường hợp 2: \(\alpha < {90^o} \Rightarrow {180^o} - \alpha > {90^o}\)
M nằm bên phải trục tung
M’ nằm bên trái trục tung
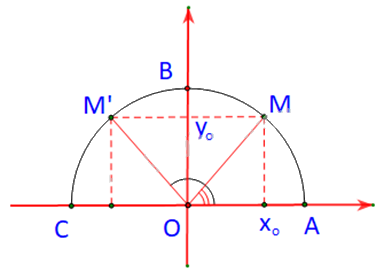
Dễ thấy: \(\widehat {M'OC} = {180^o} - \widehat {xOM'} = {180^o} - \left( {{{180}^o} - \alpha } \right) = \alpha = \widehat {xOM}\)
Suy ra \( \widehat {M'OB} = {90^o} - \widehat {M'OC} = {90^o} - \widehat {MOA} = \widehat {MOB}\)
Xét tam giác \(M'OB\) và tam giác \(MOB\) ta có:
\(OM = OM'\)
\(\widehat {M'OB} = \widehat {MOB}\)
OB chung
Suy ra \( \Delta MOB = \Delta M'OB \)
Suy ra OM = OM', BM = BM'.
Hay OB là trung trực của đoạn thẳng MM’.
Nói cách khác M và M’ đối xứng với nhau qua trục tung.
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(M'\left( { - {x_0};{y_o}} \right)\)
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Trường hợp 3: \(\alpha > {90^o} \Rightarrow {180^o} - \alpha < {90^o}\)
Khi đó M nằm bên trái trục tung và M’ nằm bên phải trục tung.
Tương tự ta cũng chứng minh được M và M’ đối xứng với nhau qua trục tung.
Như vậy
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Kết luận: Với mọi \({0^o} < \alpha < {180^o}\), ta luôn có
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha .\\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \;\;\;(\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array}\)
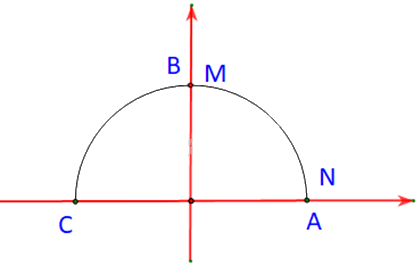
Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau \(\alpha \) và \({90^o} - \alpha \) (\(\widehat {xOM} = \alpha ,\;\;\widehat {xON} = {90^o} - \alpha \)). Chứng mình rằng \(\Delta MOP = \Delta NOQ\). Từ đó nêu mối quan hệ giữa \(\cos \alpha \) và \(\sin \left( {{{90}^o} - \alpha } \right)\).
Phương pháp giải:
Nhận xét vị trí của M và N trong mỗi trường hợp: \(\alpha = {90^o};\;\alpha < {90^o}\)
Khi \({0^o} < \alpha < {90^o}\): \(\cos \alpha ,\;\sin \alpha \) tương ứng là hoành độ và tung độ của điểm M.
Lời giải chi tiết:
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \({90^o} - \alpha = {0^o}\)
Tức là M và N lần lượt trùng nhau với B và A.
Và \(\cos \alpha = 0 = \sin \left( {{{90}^o} - \alpha } \right)\)
Trường hợp 2: \({0^o} < \alpha < {90^o} \Rightarrow {0^o} < {90^o} - \alpha < {90^0}\)
M và N cùng nằm bên trái phải trục tung.
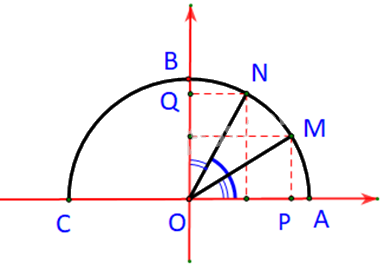
Ta có: \(\alpha = \widehat {AOM};\;\;{90^o} - \alpha = \widehat {AON}\)
Dễ thấy: \(\widehat {AON} = {90^o} - \alpha = {90^o} - \widehat {NOB}\;\;\; \Rightarrow \alpha = \widehat {NOB}\)
Xét hai tam giác vuông \(NOQ\) và tam giác \(MOP\) ta có:
\(OM = ON\)
\(\widehat {POM} = \widehat {QON}\)
Suy ra \( \Delta NOQ = \Delta MOP\)
Suy ra OP = OQ, QN = MP.
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(N\left( {{y_o};{x_0}} \right)\). Nói cách khác:
\(\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha ;\;\;\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha .\)
Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?

Phương pháp giải:
Bước 1: Giả sử chiều quay của chiếc đu quay. Xác định vị trí của cabin sau 20 phút.
Bước 2: Dựa vào giá trị lượng giác của góc, xác định khoảng cách từ cabin đến Ox (trong hình H.3.7)
Bước 3: Suy ra độ cao của người đó sau 20 phút quay.
Lời giải chi tiết:
Giả sử chiếc đu quay quay theo chiều kim đồng hồ.
Gọi M là vị trí của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A A’, B, H như hình dưới.
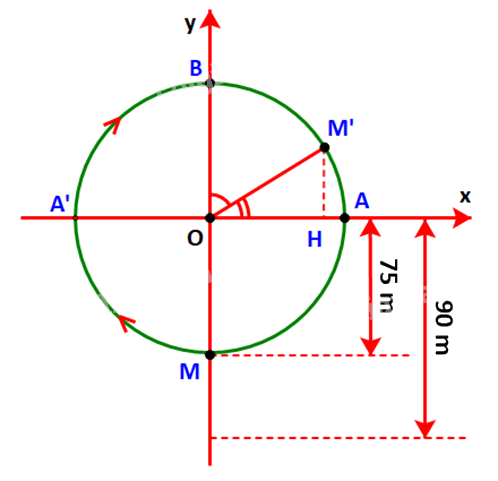
Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng \(\frac{2}{3}\) chu vi đường tròn.
Sau 15 phút cabin đi chuyển từ điểm M đến điểm B, đi được \(\frac{1}{2}\) chu vi đường tròn.
Trong 5 phút tiếp theo cabin đi chuyển từ điểm B đến điểm M’ tương ứng \(\frac{1}{6}\) chu vi đường tròn hay \(\frac{1}{3}\) cung .
Do đó: \(\widehat {BOM'} = \frac{1}{3}{.180^o} = {60^o}\)\( \Rightarrow \widehat {AOM'} = {90^o} - {60^o} = {30^o}.\)
\( \Rightarrow M'H = \sin {30^o}.OM' = \frac{1}{2}.75 = 37,5\left( m \right).\)
Suy ra độ cao của người đó là: 37,5 + 90 = 127,5 (m).
Vậy sau 20 phút quay người đó ở độ cao 127,5 m.
Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa \(\sin \alpha \) và \(\sin \left( {{{180}^o} - \alpha } \right)\), giữa \(\cos \alpha \) và \(\cos \left( {{{180}^o} - \alpha } \right)\).
Phương pháp giải:
Nhận xét vị trí của M và M’ trong mỗi trường hợp: \(\alpha = {90^o};\;\alpha < {90^o};\;\alpha > {90^o}.\)
Khi \({0^o} < \alpha < {90^o}\): \(\cos \alpha ,\;\sin \alpha \) tương ứng là hoành độ và tung độ của điểm M.
Lời giải chi tiết:
M, M’ là hai điểm trên nửa đường tròn đơn vị tương ứng với hai góc \(\alpha \) và \({180^o} - \alpha \).
Giả sử \(M\left( {{x_0};{y_o}} \right)\). Khi đó \(\cos \alpha = {x_0};\;\;\sin \alpha = {y_o}\)
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \(\alpha = {180^o} - \alpha = {90^o}\)
Tức là M và M’ lần lượt trùng nhau và trùng với B.
Và \(\left\{ \begin{array}{l}\cos \alpha = - \cos \left( {{{180}^o} - \alpha } \right) = 0;\\\sin \alpha = \sin \left( {{{180}^o} - \alpha } \right) = \sin {90^o} = 1.\\\cot \alpha = 0\end{array} \right.\)
Không tồn tại \(\tan \alpha \) với \(\alpha = {90^o}\)
Trường hợp 2: \(\alpha < {90^o} \Rightarrow {180^o} - \alpha > {90^o}\)
M nằm bên phải trục tung
M’ nằm bên trái trục tung
Dễ thấy: \(\widehat {M'OC} = {180^o} - \widehat {xOM'} = {180^o} - \left( {{{180}^o} - \alpha } \right) = \alpha = \widehat {xOM}\)
Suy ra \( \widehat {M'OB} = {90^o} - \widehat {M'OC} = {90^o} - \widehat {MOA} = \widehat {MOB}\)
Xét tam giác \(M'OB\) và tam giác \(MOB\) ta có:
\(OM = OM'\)
\(\widehat {M'OB} = \widehat {MOB}\)
OB chung
Suy ra \( \Delta MOB = \Delta M'OB \)
Suy ra OM = OM', BM = BM'.
Hay OB là trung trực của đoạn thẳng MM’.
Nói cách khác M và M’ đối xứng với nhau qua trục tung.
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(M'\left( { - {x_0};{y_o}} \right)\)
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Trường hợp 3: \(\alpha > {90^o} \Rightarrow {180^o} - \alpha < {90^o}\)
Khi đó M nằm bên trái trục tung và M’ nằm bên phải trục tung.
Tương tự ta cũng chứng minh được M và M’ đối xứng với nhau qua trục tung.
Như vậy
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Kết luận: Với mọi \({0^o} < \alpha < {180^o}\), ta luôn có
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha .\\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \;\;\;(\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array}\)
Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau \(\alpha \) và \({90^o} - \alpha \) (\(\widehat {xOM} = \alpha ,\;\;\widehat {xON} = {90^o} - \alpha \)). Chứng mình rằng \(\Delta MOP = \Delta NOQ\). Từ đó nêu mối quan hệ giữa \(\cos \alpha \) và \(\sin \left( {{{90}^o} - \alpha } \right)\).
Phương pháp giải:
Nhận xét vị trí của M và N trong mỗi trường hợp: \(\alpha = {90^o};\;\alpha < {90^o}\)
Khi \({0^o} < \alpha < {90^o}\): \(\cos \alpha ,\;\sin \alpha \) tương ứng là hoành độ và tung độ của điểm M.
Lời giải chi tiết:
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \({90^o} - \alpha = {0^o}\)
Tức là M và N lần lượt trùng nhau với B và A.
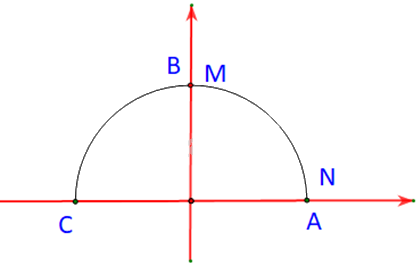
Và \(\cos \alpha = 0 = \sin \left( {{{90}^o} - \alpha } \right)\)
Trường hợp 2: \({0^o} < \alpha < {90^o} \Rightarrow {0^o} < {90^o} - \alpha < {90^0}\)
M và N cùng nằm bên trái phải trục tung.
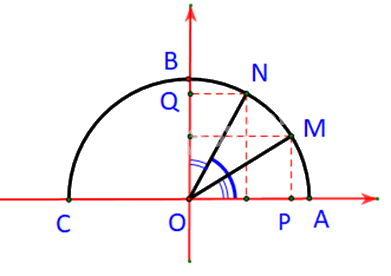
Ta có: \(\alpha = \widehat {AOM};\;\;{90^o} - \alpha = \widehat {AON}\)
Dễ thấy: \(\widehat {AON} = {90^o} - \alpha = {90^o} - \widehat {NOB}\;\;\; \Rightarrow \alpha = \widehat {NOB}\)
Xét hai tam giác vuông \(NOQ\) và tam giác \(MOP\) ta có:
\(OM = ON\)
\(\widehat {POM} = \widehat {QON}\)
Suy ra \( \Delta NOQ = \Delta MOP\)
Suy ra OP = OQ, QN = MP.
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(N\left( {{y_o};{x_0}} \right)\). Nói cách khác:
\(\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha ;\;\;\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha .\)
Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?

Phương pháp giải:
Bước 1: Giả sử chiều quay của chiếc đu quay. Xác định vị trí của cabin sau 20 phút.
Bước 2: Dựa vào giá trị lượng giác của góc, xác định khoảng cách từ cabin đến Ox (trong hình H.3.7)
Bước 3: Suy ra độ cao của người đó sau 20 phút quay.
Lời giải chi tiết:
Giả sử chiếc đu quay quay theo chiều kim đồng hồ.
Gọi M là vị trí của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A A’, B, H như hình dưới.
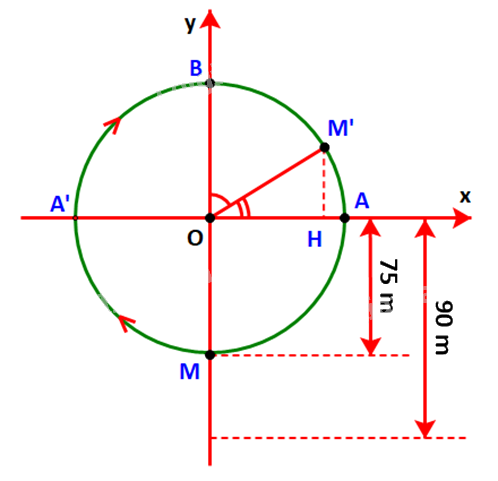
Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng \(\frac{2}{3}\) chu vi đường tròn.
Sau 15 phút cabin đi chuyển từ điểm M đến điểm B, đi được \(\frac{1}{2}\) chu vi đường tròn.
Trong 5 phút tiếp theo cabin đi chuyển từ điểm B đến điểm M’ tương ứng \(\frac{1}{6}\) chu vi đường tròn hay \(\frac{1}{3}\) cung .
Do đó: \(\widehat {BOM'} = \frac{1}{3}{.180^o} = {60^o}\)\( \Rightarrow \widehat {AOM'} = {90^o} - {60^o} = {30^o}.\)
\( \Rightarrow M'H = \sin {30^o}.OM' = \frac{1}{2}.75 = 37,5\left( m \right).\)
Suy ra độ cao của người đó là: 37,5 + 90 = 127,5 (m).
Vậy sau 20 phút quay người đó ở độ cao 127,5 m.
Mục 2 của chương trình Toán 10 tập 1 Kết nối tri thức tập trung vào các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học toán ở các lớp trên. Bài viết này sẽ đi sâu vào từng bài tập trong mục 2 trang 36, 37, cung cấp lời giải chi tiết và dễ hiểu.
Bài 1 yêu cầu học sinh xác định các tập hợp, thực hiện các phép toán hợp, giao, hiệu và phần bù của tập hợp. Để giải bài tập này, học sinh cần nắm vững định nghĩa của từng phép toán và áp dụng chúng một cách linh hoạt.
Bài 2 tập trung vào việc chứng minh các tính chất của phép hợp, giao, hiệu và phần bù của tập hợp, như tính giao hoán, tính kết hợp, tính phân phối. Để giải bài tập này, học sinh cần sử dụng các định nghĩa và tính chất đã học để chứng minh các đẳng thức.
Ví dụ 2: Chứng minh rằng A ∪ B = B ∪ A.
Lời giải: Để chứng minh A ∪ B = B ∪ A, ta cần chứng minh rằng mọi phần tử thuộc A ∪ B thì cũng thuộc B ∪ A và ngược lại.
Do đó, A ∪ B = B ∪ A.
Bài 3 yêu cầu học sinh sử dụng kiến thức về tập hợp để giải quyết các bài toán thực tế. Các bài toán này thường liên quan đến việc phân loại, sắp xếp và lựa chọn các đối tượng theo một tiêu chí nhất định.
Ví dụ 3: Trong một lớp học có 30 học sinh, có 15 học sinh thích môn Toán, 10 học sinh thích môn Văn và 5 học sinh thích cả hai môn. Hỏi có bao nhiêu học sinh không thích môn Toán và không thích môn Văn?
Lời giải: Gọi T là tập hợp các học sinh thích môn Toán, V là tập hợp các học sinh thích môn Văn. Ta có |T| = 15, |V| = 10, |T ∩ V| = 5. Số học sinh thích ít nhất một trong hai môn là |T ∪ V| = |T| + |V| - |T ∩ V| = 15 + 10 - 5 = 20. Vậy số học sinh không thích môn Toán và không thích môn Văn là 30 - 20 = 10.
Việc giải các bài tập trong mục 2 trang 36, 37 SGK Toán 10 tập 1 Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán. Hy vọng rằng với lời giải chi tiết và dễ hiểu mà chúng tôi cung cấp, các bạn học sinh sẽ tự tin hơn trong việc giải quyết các bài toán về tập hợp và các phép toán trên tập hợp.