Bài 7.37 trang 59 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết vấn đề.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.37 trang 59 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Một cột trụ hình hypebol (H.736), có chiều cao 6 m, chỗ nhỏ nhất
Đề bài
Một cột trụ hình hypebol (H.736), có chiều cao 6 m, chỗ nhỏ nhất
chính giữa và rộng 0,8 m, đỉnh cột và đáy cột đều rộng 1m. Tính độ rộng của cột ở độ cao 5 m (tính theo đơn vị mét và làm tròn tới hai chữ số sau dấu phẩy).
Lời giải chi tiết
Chọn hệ trục tọa độ sao cho gốc tọa độ trùng với điểm chính giữa hai cột, trục Oy đi qua điểm chính giữa, hai bên cột lần lượt nằm về hai phía của trục tung (như hình vẽ).
Phương trình hypebol (H) có dạng: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (với a, b>0)
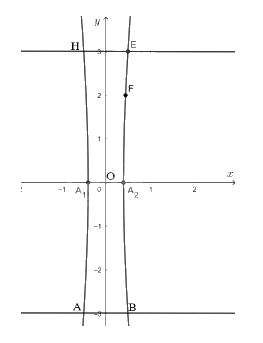
Theo bài ra ta có: A1A2 = 0,8 m; AB = EH = 1 m. Khoảng cách giữa HE và AB là 6 m.
(H) cắt trục hoành tại hai điểm A1, A2, ta xác định được tọa độ 2 điểm là: A1(− 0,4; 0) và A2(0,4; 0).
Thay tọa độ A2 vào phương trình (H) ta được: \(\frac{{0,{4^2}}}{{{a^2}}} - \frac{{{0^2}}}{{{b^2}}} = 1\)
Suy ra a=0,4 (vì a>0)
Ta xác định được tọa độ điểm E là E(0,5; 3).
(H) đi qua điểm có tọa độ E(0,5; 3) nên: \(\frac{{0,{5^2}}}{{0,{4^2}}} - \frac{{{3^2}}}{{{b^2}}} = 1\)
⇔ b2 = 16 ⇒ b = 4 (do b > 0).
Vậy phương trình (H) là: \(\frac{{{x^2}}}{{0,{4^2}}} - \frac{{{y^2}}}{{{4^2}}} = 1\) hay \(\frac{{{x^2}}}{{0,16}} - \frac{{{y^2}}}{{16}} = 1\)
Gọi F là điểm thuộc hypebol mà cột có độ cao 5 m. Ở độ cao 5 m thì khoảng cách từ vị trí F đó đến trục hoành là 2 m, tương ứng ta có tung độ điểm F là y = 2, ta cần tìm hoành độ của F.
Thay y = 2 vào phương trình (H) ta có: \(\frac{{{x^2}}}{{0,16}} - \frac{{{2^2}}}{{16}} = 1\)
⇔ x2 = 0,2 ⇔ x ≈ ± 0,45.
Vậy độ rộng của cột là: 0,45.2=0,9m (độ rộng là khoảng cách nên phải dương).
Bài 7.37 trang 59 SGK Toán 10 – Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bài tập 7.37 yêu cầu học sinh chứng minh một đẳng thức vectơ liên quan đến các điểm trong không gian. Cụ thể, bài tập thường cho một hình hộp hoặc một tứ diện và yêu cầu chứng minh mối quan hệ giữa các vectơ tạo bởi các đỉnh của hình đó.
Để giải bài tập này, ta thường sử dụng các quy tắc cộng, trừ vectơ và các tính chất của tích vô hướng. Dưới đây là một ví dụ về cách giải bài tập tương tự:
Ví dụ: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: overrightarrow{AB} +overrightarrow{AD} +overrightarrow{AA'} =overrightarrow{AC'}"
Lời giải:
Ta có: overrightarrow{AC'} =overrightarrow{AB} +overrightarrow{BC'}"
Mà overrightarrow{BC'} =overrightarrow{BD} +overrightarrow{DC'}"
Và overrightarrow{DC'} =overrightarrow{DA'} +overrightarrow{A'C'}"
Do đó: overrightarrow{AC'} =overrightarrow{AB} +overrightarrow{BD} +overrightarrow{DA'} +overrightarrow{A'C'}"
Ta có: overrightarrow{BD} =overrightarrow{AD} -overrightarrow{AB}" và overrightarrow{DA'} =overrightarrow{AA'}"
Thay vào biểu thức trên, ta được: overrightarrow{AC'} =overrightarrow{AB} + (overrightarrow{AD} -overrightarrow{AB}) +overrightarrow{AA'} +overrightarrow{A'C'}"
Suy ra: overrightarrow{AC'} =overrightarrow{AD} +overrightarrow{AA'}" (Điều phải chứng minh)
Để củng cố kiến thức về vectơ, các em học sinh có thể luyện tập thêm các bài tập tương tự trong SGK Toán 10 – Kết nối tri thức và các tài liệu tham khảo khác. Giaitoan.edu.vn sẽ tiếp tục cập nhật lời giải chi tiết cho các bài tập còn lại trong chương trình học.
Kiến thức về vectơ là nền tảng quan trọng cho các chương trình học Toán ở các lớp trên, đặc biệt là hình học không gian và giải tích. Việc nắm vững kiến thức về vectơ sẽ giúp các em học sinh giải quyết các bài toán phức tạp một cách dễ dàng và hiệu quả hơn.
Giaitoan.edu.vn là website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán từ lớp 6 đến lớp 12. Chúng tôi luôn cố gắng mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em học Toán một cách hiệu quả và thú vị.