Chào mừng các em học sinh đến với lời giải chi tiết bài 4.39 trang 72 SGK Toán 10 – Kết nối tri thức trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho các em học sinh trên con đường chinh phục môn Toán.
Trên sông, một cano chuyển động thẳng đều theo hướng S15E với vận tốc có độ lớn bằng 20 km/h. Tính vận tốc riêng của cano, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.
Đề bài
Trên sông, một cano chuyển động thẳng đều theo hướng \(S{15^o}E\) với vận tốc có độ lớn bằng 20 km/h. Tính vận tốc riêng của cano, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.
Phương pháp giải - Xem chi tiết
Định lí cosin trong tam giác OAC: \(A{C^2} = O{A^2} + O{C^2} - 2.OA.OC.\cos \widehat {AOC}\)
Lời giải chi tiết
Lấy các điểm: A, C sao cho:
Vectơ vận tốc dòng nước\(\overrightarrow {{v_n}} = \overrightarrow {OA} \)
Vectơ vận tốc chuyển động \(\overrightarrow {{v_{cano}}} = \overrightarrow {OC} \)
Ta có: \(\overrightarrow {{v_{cano}}} = \overrightarrow {{v_n}} + \overrightarrow v \), với \(\overrightarrow v \) là vectơ vận tốc riêng của cano.
Gọi B là điểm sao cho \(\overrightarrow v = \overrightarrow {OB} \) thì OACB là hình bình hành.
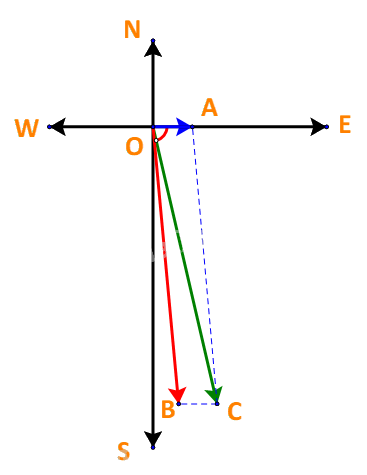
Vì tàu chuyển động theo hướng \(S{15^o}E\) nên vectơ \(\overrightarrow {OC} \) tạo với hướng Nam (tia OS) góc \({15^o}\) và tạo với hướng Đông (tia OE) góc \({90^o} - {15^o} = {75^o}\).
Mà nước trên sông chảy về hướng đông nên vectơ \(\overrightarrow {OA} \) cùng hướng với vectơ \(\overrightarrow {OE} \)
Do đó góc tạo bởi vectơ \(\overrightarrow {OC} \) và vectơ \(\overrightarrow {OA} \) là \({75^o}\)
Xét tam giác OAC ta có:
\(OA = \;|\overrightarrow {{v_n}} |\; = 3\); \(OC = \;|\overrightarrow {{v_{cano}}} |\; = 20\) và \(\widehat {AOC} = {75^o}\)
Áp dụng định lí cosin tại đỉnh O ta được:
\(\begin{array}{l}A{C^2} = O{A^2} + O{C^2} - 2.OA.OC.\cos \widehat {AOC}\\ \Leftrightarrow A{C^2} = {3^2} + {20^2} - 2.3.20.\cos {75^o} \approx 378\\ \Leftrightarrow OB = AC \approx 19,44\end{array}\)
Vậy vận tốc riêng của cano là 19,44 km/h
Bài 4.39 trang 72 SGK Toán 10 – Kết nối tri thức thuộc chương trình học về vectơ trong mặt phẳng. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài tập 4.39 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng bước giải cụ thể. (Nội dung giải chi tiết bài tập sẽ được trình bày tại đây, bao gồm các bước giải, công thức sử dụng, và giải thích rõ ràng từng bước. Ví dụ:)
Ví dụ: Cho A(1; 2), B(3; 4). Tìm tọa độ của vectơ AB.
Giải:
Vectơ AB có tọa độ là: AB = (3 - 1; 4 - 2) = (2; 2).
Ngoài bài 4.39, còn rất nhiều bài tập tương tự liên quan đến vectơ và tích vô hướng. Để giải quyết các bài tập này, học sinh cần:
Vectơ và tích vô hướng là những khái niệm quan trọng trong hình học và vật lý. Chúng được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết bài 4.39 trang 72 SGK Toán 10 – Kết nối tri thức và các bài tập tương tự. Chúc các em học tập tốt!
| Khái niệm | Định nghĩa |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Tích vô hướng | Một phép toán giữa hai vectơ, cho ra một số thực. |
| Bảng tóm tắt các khái niệm quan trọng. | |