Chào mừng bạn đến với bài học về Lý thuyết Tích vô hướng của hai vecto, một phần quan trọng trong chương trình Toán 10 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn kiến thức cơ bản, công thức và ứng dụng của tích vô hướng, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online tốt nhất với nội dung được trình bày rõ ràng, dễ hiểu và có nhiều bài tập thực hành để củng cố kiến thức.
1. GÓC GIỮA HAI VECTO 2. TÍCH VÔ HƯỚNG CỦA HAI VECTO 3. BIỂU THỨC TỌA ĐỘ VÀ TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG
1. GÓC GIỮA HAI VECTO
Cho hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) khác \(\overrightarrow 0 \). Góc giữa hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) , kí hiệu \(\left( {\;\overrightarrow u ,\overrightarrow v } \right)\)
a) Cách xác định góc: Chọn điểm A bất kì, vẽ \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}\).
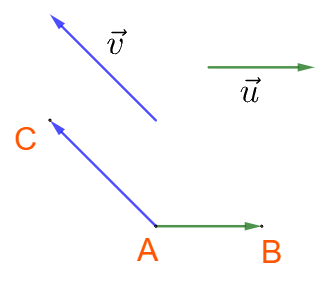
b) Các trường hợp đặc biệt:
+) \(\left( {\;\overrightarrow u ,\overrightarrow 0 } \right) = \alpha \) tùy ý, với \({0^ \circ } \le \alpha \le {180^ \circ }\)
+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u \bot \overrightarrow v \) hoặc \(\overrightarrow v \bot \overrightarrow u \). Đặc biệt: \(\overrightarrow 0 \bot \overrightarrow u \;\;\forall \overrightarrow u \;\)
+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) cùng hướng
+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) ngược hướng
2. TÍCH VÔ HƯỚNG CỦA HAI VECTO
+) Tích vô hướng của hai vecto \(\overrightarrow u ,\;\overrightarrow v \): \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
+) \(\overrightarrow u .\;\overrightarrow v \;\; = 0 \Leftrightarrow \overrightarrow u \bot \;\overrightarrow v \;\;\)
+) \(\overrightarrow u .\;\overrightarrow u \;\; = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}\)
3. BIỂU THỨC TỌA ĐỘ VÀ TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG
a) Biểu thức tọa độ của tích vô hướng
Cho \(\overrightarrow u (x;y)\) và \(\overrightarrow v = (x';y')\).
Khi đó \(\overrightarrow u .\;\overrightarrow v \;\; = xx' + yy'\)
Hệ quả:
+) \(\overrightarrow u \bot \;\overrightarrow v \; \Leftrightarrow xx' + yy' = 0\)
+) \({\overrightarrow u ^2} = \overrightarrow u .\;\overrightarrow u \;\; = x.x + y.y = {x^2} + {y^2}\)
+) Tìm góc giữa hai vecto: \(\cos \left( {\;\overrightarrow u ,\overrightarrow v } \right) = \frac{{\;\overrightarrow u .\overrightarrow v }}{{\;\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{xx' + yy'}}{{\sqrt {{x^2} + {y^2}} .\sqrt {x{'^2} + y{'^2}} }}\)
b) Công thức tính tích vô hướng khi biết độ dài:
Theo định lí cosin: \(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = A{B^2} + A{C^2} - B{C^2}\)
c) Tính chất
Cho 3 vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) bất kì và mọi số thực k, ta có:
\(\begin{array}{l}\overrightarrow u .\;\overrightarrow v \;\; = \overrightarrow v .\;\overrightarrow u \;\\\overrightarrow u .\;\left( {\overrightarrow v + \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; + \overrightarrow u .\;\overrightarrow w \;\\\left( {k\overrightarrow u } \right).\overrightarrow v = k.\left( {\overrightarrow u .\;\overrightarrow v \;} \right) = \overrightarrow u .\;\left( {k\overrightarrow v \;} \right)\end{array}\)
Hệ quả
\(\begin{array}{l}\overrightarrow u .\;\left( {\overrightarrow v - \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; - \overrightarrow u .\;\overrightarrow w \\{\left( {\overrightarrow u + \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} + 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2};\;\;{\left( {\overrightarrow u - \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} - 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2}\\\left( {\overrightarrow u + \overrightarrow v } \right)\left( {\overrightarrow u - \overrightarrow v } \right) = {\overrightarrow u ^2} - {\overrightarrow v ^2}\end{array}\)
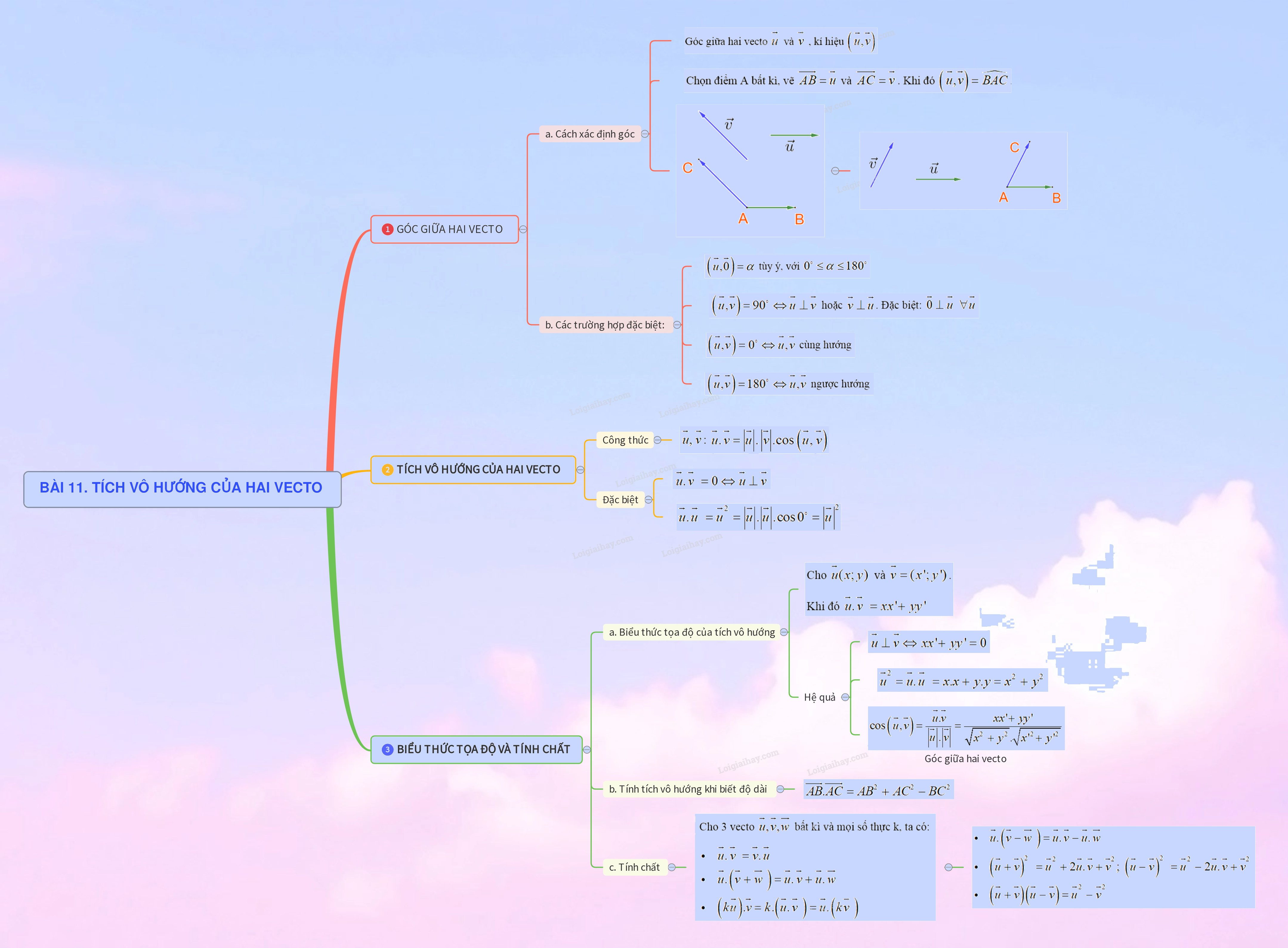
Tích vô hướng của hai vectơ là một khái niệm quan trọng trong hình học vectơ, đóng vai trò nền tảng cho nhiều ứng dụng trong toán học và vật lý. Bài viết này sẽ trình bày chi tiết lý thuyết về tích vô hướng, bao gồm định nghĩa, tính chất, công thức tính và các ứng dụng thực tế, dựa trên chương trình Toán 10 Kết nối tri thức.
Cho hai vectơ a và b. Tích vô hướng của a và b, ký hiệu là a ⋅ b, là một số thực được tính theo công thức:
a ⋅ b = |a| |b| cos(θ)
Trong đó:
Tích vô hướng có những tính chất quan trọng sau:
Nếu a = (x1; y1) và b = (x2; y2) trong hệ tọa độ Oxy, thì:
a ⋅ b = x1x2 + y1y2
Tổng quát, trong không gian Oxyz, nếu a = (x1; y1; z1) và b = (x2; y2; z2), thì:
a ⋅ b = x1x2 + y1y2 + z1z2
Tích vô hướng có nhiều ứng dụng quan trọng trong toán học và vật lý, bao gồm:
Ví dụ 1: Cho a = (2; -1) và b = (1; 3). Tính a ⋅ b.
Giải: a ⋅ b = 2 * 1 + (-1) * 3 = 2 - 3 = -1
Ví dụ 2: Cho a = (1; 2; 3) và b = (-1; 0; 2). Tính a ⋅ b.
Giải: a ⋅ b = 1 * (-1) + 2 * 0 + 3 * 2 = -1 + 0 + 6 = 5
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Tích vô hướng của hai vecto - SGK Toán 10 Kết nối tri thức. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.