Bài 3.13 trang 44 SGK Toán 10 tập 1 thuộc chương 3: Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC. Khẳng định nào sau đây là đúng?
A. \(\sin A = \sin \,(B + C)\)
B. \(\cos A = \cos \,(B + C)\)
C. \(\;\cos A > 0\)
D. \(\sin A\,\, \le 0\)
Phương pháp giải:
Giá trị lượng giác của hai góc bù nhau:
\(\sin x = \sin \left( {{{180}^o} - x} \right)\); \( - \cos x = \cos \left( {{{180}^o} - x} \right)\)
Lời giải chi tiết:
A. \(\sin A = \sin \,(B + C)\)
Ta có: \((\widehat A + \widehat C) + \widehat B= {180^o}\)
\(\Rightarrow \sin \,(B + C) = \sin A\)
=> A đúng.
B. \(\cos A = \cos \,(B + C)\)
Sai vì \(\cos \,(B + C) = - \cos A\)
C. \(\;\cos A > 0\) Không đủ dữ kiện để kết luận.
Nếu \({0^o} < \widehat A < {90^o}\) thì \(\cos A > 0\)
Nếu \({90^o} < \widehat A < {180^o}\) thì \(\cos A < 0\)
D. \(\sin A\,\, \le 0\)
Ta có \(S = \frac{1}{2}bc.\sin A > 0\). Mà \(b,c > 0\)
\( \Rightarrow \sin A > 0\)
=> D sai.
Chọn A
A. \(S = \frac{{abc}}{{4r}}\)
B. \(r = \frac{{2S}}{{a + b + c}}\)
C. \({a^2} = {b^2} + {c^2} + 2bc\;\cos A\)
D. \(S = r\,(a + b + c)\)
Phương pháp giải:
+) Định lí cos: \({a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
+) Công thức tính diện tích: \(S = pr = \frac{{abc}}{{4R}}\)
Lời giải chi tiết:
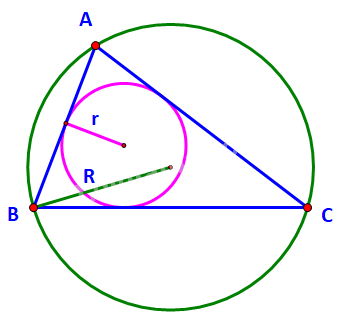
A. \(S = \frac{{abc}}{{4r}}\)
Ta có: \(S = \frac{{abc}}{{4R}}\). Mà \(r < R\) nên suy ra \(S = \frac{{abc}}{{4R}} < \frac{{abc}}{{4r}}\)
Vậy A sai.
B. \(r = \frac{{2S}}{{a + b + c}}\)
Ta có: \(S = pr \Rightarrow r = \frac{S}{p}\)
Mà \(p = \frac{{a + b + c}}{2}\;\; \Rightarrow r = \frac{S}{p}\; = \frac{S}{{\frac{{a + b + c}}{2}}} = \frac{{2S}}{{a + b + c}}\;\)
Vậy B đúng.
C. \({a^2} = {b^2} + {c^2} + 2bc\;\cos A\)
Sai vì theo định lí cos ta có: \({a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
D. \(S = r\,(a + b + c)\)
Sai vì \(S = pr = r.\frac{{a + b + c}}{2}\)
Chọn B
Cho tam giác ABC. Khẳng định nào sau đây là đúng?
A. \(S = \frac{{abc}}{{4r}}\)
B. \(r = \frac{{2S}}{{a + b + c}}\)
C. \({a^2} = {b^2} + {c^2} + 2bc\;\cos A\)
D. \(S = r\,(a + b + c)\)
Phương pháp giải:
+) Định lí cos: \({a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
+) Công thức tính diện tích: \(S = pr = \frac{{abc}}{{4R}}\)
Lời giải chi tiết:
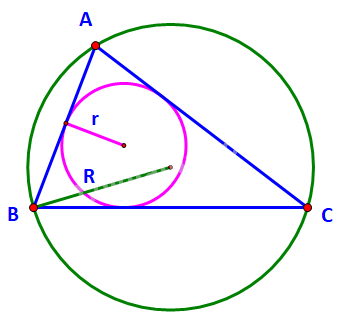
A. \(S = \frac{{abc}}{{4r}}\)
Ta có: \(S = \frac{{abc}}{{4R}}\). Mà \(r < R\) nên suy ra \(S = \frac{{abc}}{{4R}} < \frac{{abc}}{{4r}}\)
Vậy A sai.
B. \(r = \frac{{2S}}{{a + b + c}}\)
Ta có: \(S = pr \Rightarrow r = \frac{S}{p}\)
Mà \(p = \frac{{a + b + c}}{2}\;\; \Rightarrow r = \frac{S}{p}\; = \frac{S}{{\frac{{a + b + c}}{2}}} = \frac{{2S}}{{a + b + c}}\;\)
Vậy B đúng.
C. \({a^2} = {b^2} + {c^2} + 2bc\;\cos A\)
Sai vì theo định lí cos ta có: \({a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
D. \(S = r\,(a + b + c)\)
Sai vì \(S = pr = r.\frac{{a + b + c}}{2}\)
Chọn B
A. \(\sin A = \sin \,(B + C)\)
B. \(\cos A = \cos \,(B + C)\)
C. \(\;\cos A > 0\)
D. \(\sin A\,\, \le 0\)
Phương pháp giải:
Giá trị lượng giác của hai góc bù nhau:
\(\sin x = \sin \left( {{{180}^o} - x} \right)\); \( - \cos x = \cos \left( {{{180}^o} - x} \right)\)
Lời giải chi tiết:
A. \(\sin A = \sin \,(B + C)\)
Ta có: \((\widehat A + \widehat C) + \widehat B= {180^o}\)
\(\Rightarrow \sin \,(B + C) = \sin A\)
=> A đúng.
B. \(\cos A = \cos \,(B + C)\)
Sai vì \(\cos \,(B + C) = - \cos A\)
C. \(\;\cos A > 0\) Không đủ dữ kiện để kết luận.
Nếu \({0^o} < \widehat A < {90^o}\) thì \(\cos A > 0\)
Nếu \({90^o} < \widehat A < {180^o}\) thì \(\cos A < 0\)
D. \(\sin A\,\, \le 0\)
Ta có \(S = \frac{1}{2}bc.\sin A > 0\). Mà \(b,c > 0\)
\( \Rightarrow \sin A > 0\)
=> D sai.
Chọn A
Bài 3.13 trang 44 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và ứng dụng của nó trong việc mô tả các tình huống thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Một người nông dân trồng cây cam. Chi phí trồng và chăm sóc cây cam là 10 triệu đồng. Mỗi quả cam bán được với giá 5000 đồng. Gọi x là số quả cam người đó thu hoạch được. Hãy viết hàm số biểu thị lợi nhuận thu được khi bán x quả cam.)
Lời giải:
Để hiểu rõ hơn về cách giải bài tập về hàm số bậc nhất, chúng ta hãy xem xét một ví dụ minh họa sau:
Ví dụ: Một cửa hàng bán lẻ mua một lô hàng với giá 50 triệu đồng. Mỗi sản phẩm bán được với giá 100.000 đồng. Gọi x là số sản phẩm cửa hàng bán được. Hãy viết hàm số biểu thị lợi nhuận thu được khi bán x sản phẩm.
Lời giải: Tương tự như bài 3.13, ta có:
Doanh thu = 100.000x
Lợi nhuận = 100.000x - 50.000.000
Hàm số biểu thị lợi nhuận: f(x) = 100.000x - 50.000.000
Khi giải các bài tập về hàm số bậc nhất, học sinh cần chú ý:
Bài 3.13 trang 44 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về bài tập này và tự tin làm bài tập.