Bài 6.22 trang 27 SGK Toán 10 Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.22 trang 27 SGK Toán 10 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
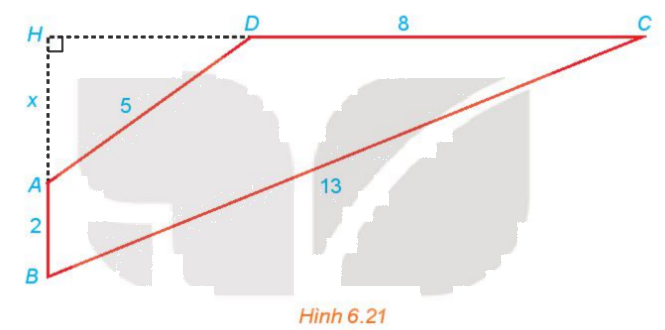
(H.6.21). Gọi H là giao điểm của AB và CD và đặt x=AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD
Đề bài
Cho từ giác ABCD có \(AB \bot CD;AB = 2;BC = 13;CD = 8;DA = 5\) (H.6.21). Gọi H là giao điểm của AB và CD và đặt x=AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD
Phương pháp giải - Xem chi tiết
Bước 1: Tính HD,HC theo x
Bước 2: Sử dụng định lý py-ta-go cho tam giác vuông BHC
\(B{C^2} = H{B^2} + H{C^2}\)
Khi đó ta lập được phương trình \(4\sqrt {25 - {x^2}} = - x + 19\)
Bước 3: Giải phương trình trên ta tìm được x
Lời giải chi tiết
Ta có :AH=x (x>0)
Xét tam giác AHD vuông ở H, ta có:
\(A{D^2} = A{H^2} + H{D^2} \Leftrightarrow H{D^2} = A{D^2} - A{H^2} = 25 - {x^2}\)
\( \Rightarrow HD = \sqrt {25 - {x^2}} \)
Ta có: \(HC = HD + DC = \sqrt {25 - {x^2}} + 8\)
\(HB = AH + AB = x + 2\)
Xét tam giác HBC vuông tại H, ta có:
\(\begin{array}{l}B{C^2} = H{B^2} + H{C^2}\\ \Leftrightarrow {13^2} = {(x + 2)^2} + {\left( {\sqrt {25 - {x^2}} + 8} \right)^2}\\ \Leftrightarrow 169 = {x^2} + 4x + 4 + 25 - {x^2} + 16\sqrt {25 - {x^2}} + 64\\ \Leftrightarrow 16\sqrt {25 - {x^2}} = - 4x + 76\\ \Leftrightarrow 4\sqrt {25 - {x^2}} = - x + 19\end{array}\)
Bình phương hai vế của phương trình trên ta được:
\(\begin{array}{l}16(25 - {x^2}) = {x^2} - 38x + 361\\ \Leftrightarrow 17{x^2} - 38x - 39 = 0\end{array}\)
\( \Leftrightarrow x = 3\) hoặc \(x = \frac{{ - 13}}{{17}}\)
Thay lần lượt các giá trị trên vào phương trình, ta thấy hai giá trị đều thỏa mãn
Do x>0 nên ta chọn x=3 => AH=3
\(\begin{array}{l}HD = \sqrt {25 - {3^2}} = 4\\HC = 4 + 8 = 12\\HB = 3 + 2 = 5\end{array}\)
Diện tích tam giác HAD là \({S_1} = \frac{1}{2}.HA.HD = \frac{1}{2}.3.4 = 6\)
Diện tích tam giác HBC là \({S_2} = \frac{1}{2}.HB.HC = \frac{1}{2}.5.12 = 30\)
Vậy diện tích tứ giác ABCD là \(S = {S_2} - {S_1} = 30 - 6 = 24\)
Bài 6.22 trang 27 SGK Toán 10 – Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản sau:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho tam giác ABC, tìm tập hợp các điểm M thỏa mãn MA + MB = MC)
Lời giải:
Ví dụ minh họa: (Giải chi tiết bài toán với các bước cụ thể, sử dụng hình vẽ minh họa nếu cần)
Ngoài bài 6.22, còn rất nhiều bài tập tương tự liên quan đến vectơ trong không gian. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, các em học sinh có thể tham khảo thêm các bài tập sau:
Bài 6.22 trang 27 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về vectơ và ứng dụng của nó trong hình học. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.