Giải bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức

Chào mừng các em học sinh đến với lời giải chi tiết bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức. Bài học này thuộc chương trình Toán 10, tập trung vào việc vận dụng kiến thức về vectơ để giải quyết các bài toán hình học.

Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết, giúp các em hiểu rõ bản chất của bài toán và tự tin làm bài tập.

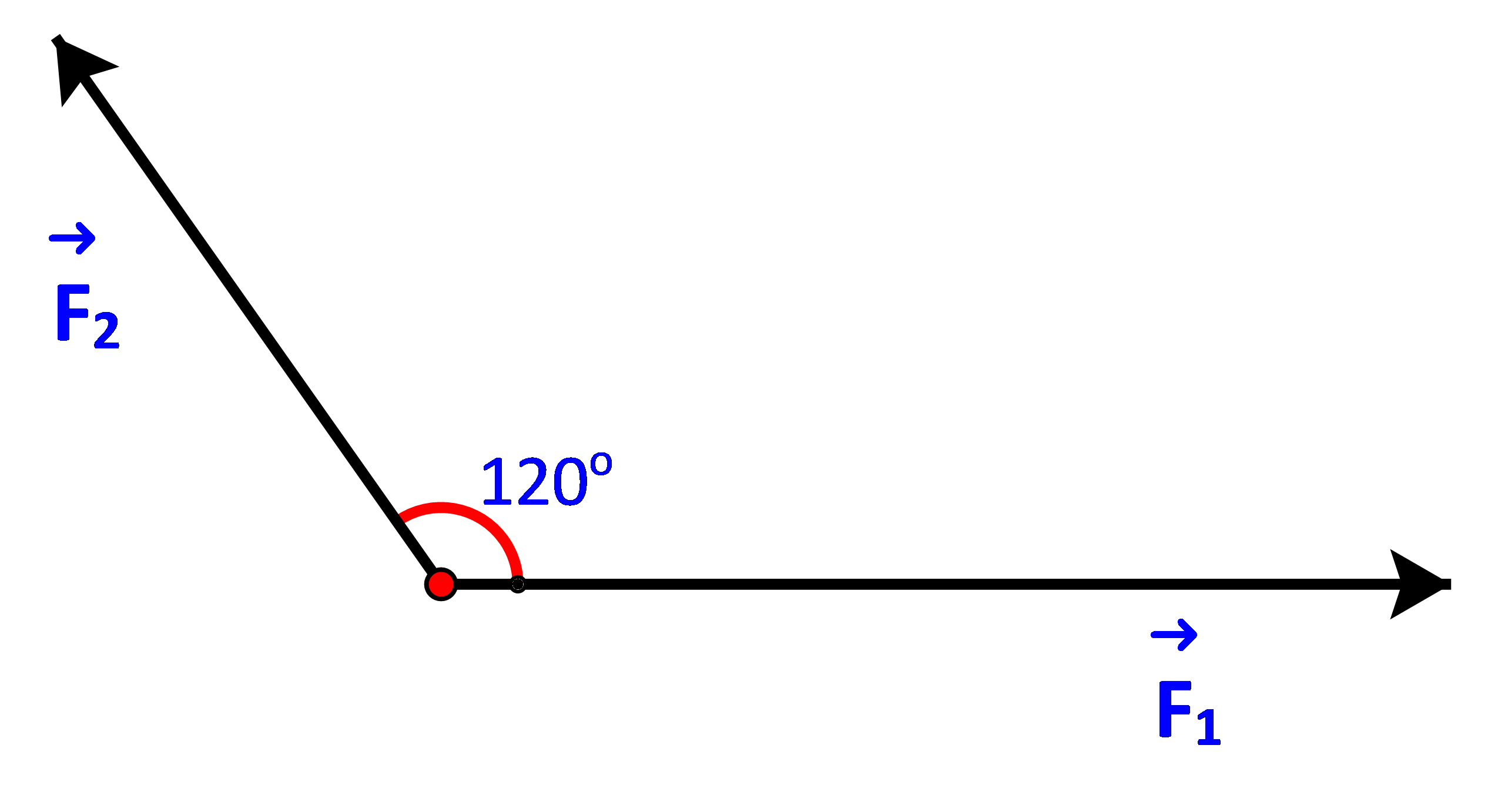
Hình 4.19 biểu diễn hai lực F1, F2 cùng tác động lên một vật, cho

Đề bài

Hình 4.19 biểu diễn hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác động lên một vật, cho \(\left| {\overrightarrow {{F_1}} } \right| = 3\;N,\;\left| {\overrightarrow {{F_2}} } \right| = 2\;N.\) Tính độ lớn của hợp lực \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \).

Giải bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức 1

Phương pháp giải - Xem chi tiết Giải bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức 2

Để tìm tổng của hai vectơ chung gốc \(\overrightarrow {AB} ,\;\overrightarrow {AD} \) ta dựng hình hình hành ABCD, khi đó:\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)

Lời giải chi tiết

Dựng hình bình hành ABCD với hai cạnh là hai vectơ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) như hình vẽ

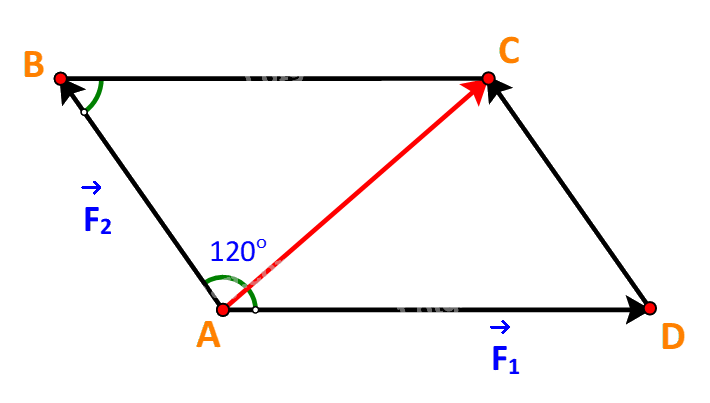
Giải bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức 3

Ta có:

\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {AD} + \overrightarrow {AB} = \overrightarrow {AC} \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AC} } \right| = AC\)

Xét \(\Delta ABC\) ta có:

\(BC = AD = \left| {\overrightarrow {{F_1}} } \right| = 3\;,AB = \;\left| {\overrightarrow {{F_2}} } \right| = 2\;.\)

\(\widehat {ABC} = {180^o} - \widehat {BAD} = {180^o} - {120^o} = {60^o}\)

Theo định lí cosin ta có:

\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}\\ \Leftrightarrow A{C^2} = {2^2} + {3^2} - 2.2.3.\cos {60^o}\\ \Leftrightarrow A{C^2} = 7\\ \Leftrightarrow AC = \sqrt {7} \end{array}\)

Vậy \(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \sqrt {7} \)

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Giải bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức đặc sắc thuộc chuyên mục giải bài tập toán 10 trên nền tảng toán học. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Giải bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức: Tóm tắt lý thuyết và phương pháp giải

Bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để chứng minh một số tính chất hình học. Để giải bài này, các em cần nắm vững các khái niệm và công thức sau:

Tích vô hướng của hai vectơ:a.b = |a||b|cos(θ), trong đó θ là góc giữa hai vectơ a và b.
Điều kiện vuông góc: Hai vectơ a và b vuông góc khi và chỉ khi a.b = 0.
Ứng dụng của tích vô hướng: Sử dụng tích vô hướng để chứng minh hai đường thẳng vuông góc, tính góc giữa hai đường thẳng, hoặc xác định tính chất của các hình đa giác.

Lời giải chi tiết bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức

Đề bài: Cho tam giác ABC có trung điểm các cạnh BC, CA, AB lần lượt là D, E, F. Chứng minh rằng AD, BE, CF đồng quy.

Lời giải:

Chọn hệ tọa độ: Đặt A(0;0), B(x_B; y_B), C(x_C; y_C).
Tìm tọa độ các điểm D, E, F:
- D là trung điểm BC: D((x_B + x_C)/2; (y_B + y_C)/2)
- E là trung điểm CA: E((x_C)/2; (y_C)/2)
- F là trung điểm AB: F((x_B)/2; (y_B)/2)
Tìm phương trình các đường thẳng AD, BE, CF:
- Đường thẳng AD đi qua A(0;0) và D((x_B + x_C)/2; (y_B + y_C)/2): Phương trình AD là y = ((y_B + y_C)/(x_B + x_C))x
- Đường thẳng BE đi qua B(x_B; y_B) và E((x_C)/2; (y_C)/2): Phương trình BE là... (tương tự)
- Đường thẳng CF đi qua C(x_C; y_C) và F((x_B)/2; (y_B)/2): Phương trình CF là... (tương tự)
Giải hệ phương trình: Giải hệ phương trình tạo bởi phương trình của hai đường thẳng bất kỳ (ví dụ AD và BE) để tìm giao điểm.
Kiểm tra: Thay tọa độ giao điểm vừa tìm được vào phương trình đường thẳng còn lại (CF) để kiểm tra xem giao điểm có nằm trên CF hay không. Nếu có, thì AD, BE, CF đồng quy.

Mở rộng và bài tập tương tự

Bài toán này là một ví dụ điển hình về việc sử dụng vectơ trong hình học. Các em có thể tìm hiểu thêm về các ứng dụng khác của tích vô hướng, chẳng hạn như:

Chứng minh các tính chất của hình bình hành, hình chữ nhật, hình thoi, hình vuông.
Tính diện tích tam giác, tứ giác.
Xác định vị trí tương đối của hai đường thẳng.

Dưới đây là một số bài tập tương tự để các em luyện tập:

Bài 4.10 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức
Bài 4.11 trang 55 SGK Toán 10 tập 1 – Kết nối tri thức
Các bài tập trắc nghiệm về tích vô hướng.

Kết luận

Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em đã hiểu rõ cách giải bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!