Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho từng bài tập trong SGK Toán 10 Kết nối tri thức, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 của chương trình Toán 10 tập 1 tập trung vào các khái niệm và bài tập về tập hợp, các phép toán trên tập hợp, và các ứng dụng của tập hợp trong thực tế.
Khi nào thì tích vô hướng của hai vectơ uv là một số dương? Là một số âm? Khi nào thì (u.v)^2 = u^2. v^2? Cho tam giác AB C có BC = a, CA = b, AB = c. Hãy tính (overrightarrow {AB} .overrightarrow {AC} ) theo a,b,c.
Khi nào thì \({\left( {\overrightarrow u .\;\overrightarrow v } \right)^2} = {\left( {\overrightarrow u } \right)^2}.{\left( {\overrightarrow v } \right)^2}\)?
Phương pháp giải:
+) \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
+) \({\overrightarrow u ^2} = {\left| {\overrightarrow u } \right|^2}\) với mọi vectơ \(\overrightarrow u \)
Lời giải chi tiết:
\({\left( {\overrightarrow u .\;\overrightarrow v } \right)^2} = {\left( {\overrightarrow u } \right)^2}.{\left( {\overrightarrow v } \right)^2}\)\( \Leftrightarrow {\left[ {\left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)} \right]^2} = {\left| {\overrightarrow u } \right|^2}.{\left| {\overrightarrow v } \right|^2}\)
\(\begin{array}{l} \Leftrightarrow {\left[ {\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)} \right]^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = 1\\\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = - 1\end{array} \right.\end{array}\)
\( \Leftrightarrow \left[ \begin{array}{l}\;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {0^o}\\\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {180^o}\end{array} \right.\)
Hay hai vectơ \(\overrightarrow u ,\;\overrightarrow v \) cùng phương.
Vậy hai vectơ \(\overrightarrow u ,\;\overrightarrow v \) cùng phương thì \({\left( {\overrightarrow u .\;\overrightarrow v } \right)^2} = {\left( {\overrightarrow u } \right)^2}.{\left( {\overrightarrow v } \right)^2}\)
Cho tam giác AB C có BC = a, CA = b, AB = c. Hãy tính \(\overrightarrow {AB} .\overrightarrow {AC} \) theo a,b,c.
Phương pháp giải:
+) Tích vô hướng: \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)
Mà \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC}\)\( \Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \cos \widehat {BAC}\)
Lại có: \(\cos \widehat {BAC} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)(suy ra từ định lí cosin)
\(\begin{array}{l} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\ \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = c.b.\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\ \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = \frac{{{b^2} + {c^2} - {a^2}}}{2}\end{array}\)
Khi nào thì tích vô hướng của hai vectơ \(\overrightarrow u ,\;\overrightarrow v \) là một số dương? Là một số âm?
Phương pháp giải:
+) Tích vô hướng của hai vectơ \(\overrightarrow u ,\;\overrightarrow v \): \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
Nhận xét: \(\overrightarrow u .\;\overrightarrow v \) cùng dấu với \(\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
Lời giải chi tiết:
Dễ thấy: \(\overrightarrow u .\;\overrightarrow v \) cùng dấu với \(\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\) (do \(\left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| > 0\)). Do đó:
+) \(\overrightarrow u .\;\overrightarrow v \;\; > 0\) \( \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) > 0\) hay \({0^o} \le \left( {\overrightarrow u ,\;\overrightarrow v } \right) < {90^o}\)
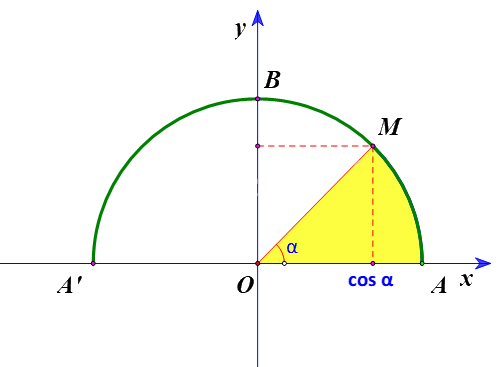
+) \(\overrightarrow u .\;\overrightarrow v \;\; < 0\) \( \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\;\; < 0\) hay \({90^o} < \left( {\overrightarrow u ,\;\overrightarrow v } \right) \le {180^o}\)
Vậy \(\overrightarrow u .\;\overrightarrow v \;\; > 0\) nếu \({0^o} \le \left( {\overrightarrow u ,\;\overrightarrow v } \right) < {90^o}\) và \(\overrightarrow u .\;\overrightarrow v \;\; < 0\) nếu \({90^o} < \left( {\overrightarrow u ,\;\overrightarrow v } \right) \le {180^o}.\)
Khi nào thì \({\left( {\overrightarrow u .\;\overrightarrow v } \right)^2} = {\left( {\overrightarrow u } \right)^2}.{\left( {\overrightarrow v } \right)^2}\)?
Phương pháp giải:
+) \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
+) \({\overrightarrow u ^2} = {\left| {\overrightarrow u } \right|^2}\) với mọi vectơ \(\overrightarrow u \)
Lời giải chi tiết:
\({\left( {\overrightarrow u .\;\overrightarrow v } \right)^2} = {\left( {\overrightarrow u } \right)^2}.{\left( {\overrightarrow v } \right)^2}\)\( \Leftrightarrow {\left[ {\left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)} \right]^2} = {\left| {\overrightarrow u } \right|^2}.{\left| {\overrightarrow v } \right|^2}\)
\(\begin{array}{l} \Leftrightarrow {\left[ {\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)} \right]^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = 1\\\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = - 1\end{array} \right.\end{array}\)
\( \Leftrightarrow \left[ \begin{array}{l}\;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {0^o}\\\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {180^o}\end{array} \right.\)
Hay hai vectơ \(\overrightarrow u ,\;\overrightarrow v \) cùng phương.
Vậy hai vectơ \(\overrightarrow u ,\;\overrightarrow v \) cùng phương thì \({\left( {\overrightarrow u .\;\overrightarrow v } \right)^2} = {\left( {\overrightarrow u } \right)^2}.{\left( {\overrightarrow v } \right)^2}\)
Cho tam giác AB C có BC = a, CA = b, AB = c. Hãy tính \(\overrightarrow {AB} .\overrightarrow {AC} \) theo a,b,c.
Phương pháp giải:
+) Tích vô hướng: \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)
Mà \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC}\)\( \Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \cos \widehat {BAC}\)
Lại có: \(\cos \widehat {BAC} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)(suy ra từ định lí cosin)
\(\begin{array}{l} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\ \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = c.b.\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\ \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = \frac{{{b^2} + {c^2} - {a^2}}}{2}\end{array}\)
Khi nào thì tích vô hướng của hai vectơ \(\overrightarrow u ,\;\overrightarrow v \) là một số dương? Là một số âm?
Phương pháp giải:
+) Tích vô hướng của hai vectơ \(\overrightarrow u ,\;\overrightarrow v \): \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
Nhận xét: \(\overrightarrow u .\;\overrightarrow v \) cùng dấu với \(\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
Lời giải chi tiết:
Dễ thấy: \(\overrightarrow u .\;\overrightarrow v \) cùng dấu với \(\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\) (do \(\left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| > 0\)). Do đó:
+) \(\overrightarrow u .\;\overrightarrow v \;\; > 0\) \( \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) > 0\) hay \({0^o} \le \left( {\overrightarrow u ,\;\overrightarrow v } \right) < {90^o}\)
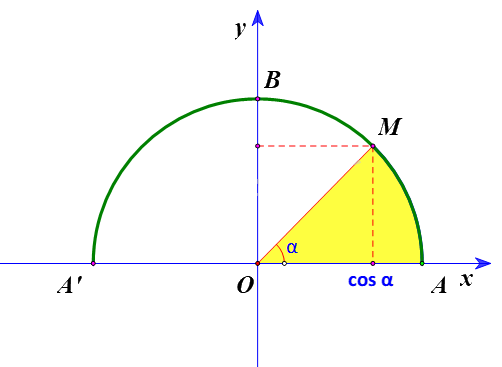
+) \(\overrightarrow u .\;\overrightarrow v \;\; < 0\) \( \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\;\; < 0\) hay \({90^o} < \left( {\overrightarrow u ,\;\overrightarrow v } \right) \le {180^o}\)
Vậy \(\overrightarrow u .\;\overrightarrow v \;\; > 0\) nếu \({0^o} \le \left( {\overrightarrow u ,\;\overrightarrow v } \right) < {90^o}\) và \(\overrightarrow u .\;\overrightarrow v \;\; < 0\) nếu \({90^o} < \left( {\overrightarrow u ,\;\overrightarrow v } \right) \le {180^o}.\)
Mục 2 trong SGK Toán 10 tập 1 Kết nối tri thức là một phần quan trọng, đặt nền móng cho các kiến thức toán học nâng cao hơn. Nội dung chính của mục này xoay quanh các khái niệm cơ bản về tập hợp, bao gồm định nghĩa tập hợp, các ký hiệu, cách biểu diễn tập hợp, và các phép toán trên tập hợp như hợp, giao, hiệu, phần bù. Việc nắm vững các khái niệm này là điều kiện tiên quyết để giải quyết các bài tập một cách chính xác và hiệu quả.
Để giải các bài tập trong Mục 2 trang 67, 68, 69, 70 SGK Toán 10 tập 1 Kết nối tri thức, các em cần:
Bài 1 (Trang 67): Cho A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Tìm A ∪ B và A ∩ B.
Giải:
Các bài tập trong Mục 2 thường gặp các dạng sau:
Để học tốt Mục 2, các em nên:
Giaitoan.edu.vn hy vọng rằng với những hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải các bài tập trong Mục 2 trang 67, 68, 69, 70 SGK Toán 10 tập 1 Kết nối tri thức. Chúc các em học tập tốt!