Chào mừng bạn đến với bài học về Lý thuyết Dấu của tam thức bậc hai, một phần quan trọng trong chương trình Toán 10 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và cần thiết để giải quyết các bài toán liên quan đến tam thức bậc hai.
Chúng ta sẽ cùng nhau tìm hiểu về định nghĩa, các yếu tố ảnh hưởng đến dấu của tam thức bậc hai, và cách xác định dấu của tam thức dựa vào nghiệm của nó. Đây là kiến thức nền tảng để giải quyết các bài toán bất phương trình bậc hai và các bài toán ứng dụng khác.
A. Lý thuyết 1. Dấu của tam thức bậc hai a) Khái niệm tam thức bậc hai
A. Lý thuyết
1. Dấu của tam thức bậc hai
a) Khái niệm tam thức bậc hai
| Tam thức bậc hai (đối với x) là biểu thức có dạng \(a{x^2} + bx + c\), trong đó a, b, c là các số thực cho trước và \(a \ne 0\), được gọi là các hệ số của tam thức bậc hai. |
Chú ý: Nghiệm của phương trình bậc hai \(a{x^2} + bx + c = 0\) cũng được gọi là nghiệm của tam thức bậc hai \(a{x^2} + bx + c\).
| \(\Delta = {b^2} - 4ac\) và \(\Delta ' = b{'^2} - ac\) với b = 2b’ tương ứng được gọi là biệt thức và biệt thức thu gọn của tam thức bậc hai \(a{x^2} + bx + c\). |
b) Dấu của tam thức bậc hai
Mối quan hệ giữa dấu của tam thức bậc hai \(a{x^2} + bx + c\) với dấu của hệ số a trong từng trường hợp của \(\Delta \) được phát biểu trong định lí về dấu của tam thức bậc hai sau đây:
Cho tam thức bậc hai \(f(x) = a{x^2} + bx + c\) \((a \ne 0)\). - Nếu \(\Delta < 0\) thì f(x) cùng dấu với hệ số a \(\forall x \in \mathbb{R}\). - Nếu \(\Delta = 0\) thì f(x) cùng dấu với hệ số a với mọi \(x \ne - \frac{b}{{2a}}\) và \(f\left( { - \frac{b}{{2a}}} \right) = 0\). - Nếu \(\Delta > 0\) thì tam thức f(x) có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) \(({x_1} < {x_2})\). Khi đó: + f(x) cùng dấu với hệ số a \(\forall x \in ( - \infty ;{x_1}) \cup ({x_2}; + \infty )\). + f(x) trái dấu với hệ số a \(\forall x \in ({x_1};{x_2})\). |

Chú ý: Trong định lí về dấu của tam thức bậc hai, có thể thay \(\Delta \) bởi \(\Delta '\).
2. Bất phương trình bậc hai
Bất phương trình bậc hai ẩn x là bất phương trình có dạng \(a{x^2} + bx + c > 0\) (hoặc \(a{x^2} + bx + c \ge 0\), \(a{x^2} + bx + c < 0\), \(a{x^2} + bx + c \le 0\)), trong đó a, b, c là những số thực đã cho và \(a \ne 0\). Số thực \({x_0}\) gọi là nghiệm của bất phương trình bậc hai \(a{x^2} + bx + c > 0\), nếu \(a{x_0}^2 + b{x_0} + c > 0\). Tập hợp gồm tất cả các nghiệm của bất phương trình bậc hai \(a{x^2} + bx + c > 0\) gọi là tập nghiệm của bất phương trình này. Giải một bất phương trình bậc hai là tìm tập nghiệm của nó. |
Nhận xét: Để giải bất phương trình bậc hai \(a{x^2} + bx + c > 0\) (hoặc \(a{x^2} + bx + c \ge 0\), \(a{x^2} + bx + c < 0\), \(a{x^2} + bx + c \le 0\)) ta cần xét dấu tam thức \(a{x^2} + bx + c\), từ đó suy ra tập nghiệm.
B. Bài tập
Bài 1: Hãy cho biết biểu thức nào sau đây là tam thức bậc hai?
A. \(3x + 2\sqrt x + 1\)
B. \( - 5{x^4} + 3{x^2} + 4\)
C. \( - \frac{2}{3}{x^2} + 7x - 4\)
D. \({\left( {\frac{1}{x}} \right)^2} + 2\frac{1}{x} + 3\)
Giải:
\( - \frac{2}{3}{x^2} + 7x - 4\) là tam thức bậc hai với \(a = - \frac{2}{3},b = 7,c = - 4\).
Bài 2: Xét dấu các tam thức bậc hai sau đây:
a) \({x^2} + x + 1\).
b) \( - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}\).
c) \(2{x^2} + 6x - 8\).
Giải:
a) \(f(x) = {x^2} + x + 1\) có \(\Delta = - 3 < 0\) và \(a = 1 > 0\) nên f(x) > 0 với mọi \(x \in \mathbb{R}\).
b)
\(f(x) = - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}\) có \(\Delta = 0\) và \(a = - \frac{3}{2} < 0\) nên f(x) có nghiệm kép x = 3 và f(x) < 0 với mọi \(x \ne 3\).
c) Dễ thấy \(f(x) = 2{x^2} + 6x - 8\) có \(\Delta ' = 25 > 0\), a = 2 > 0 và có hai nghiệm phân biệt \({x_1} = - 4\), \({x_2} = 1\). Do đó ta có bảng xét dấu:
Suy ra f(x) > 0 với mọi \(x \in ( - \infty ; - 4) \cup (1; + \infty )\) và f(x) < 0 với mọi \(x \in ( - 4;1)\).
Bài 3: Giải các bất phương trình sau:
a) \(3{x^2} + x + 5 \le 0\).
b) \( - 3{x^2} + 2\sqrt 3 x - 1 \ge 0\).
c) \( - {x^2} + 2x + 1 > 0\).
Giải:
a) Tam thức \(f(x) = 3{x^2} + x + 5\) có \(\Delta = - 59 < 0\), hệ số a = 3 > 0 0 nên f(x) luôn dương (cùng dấu với a) với mọi x, tức là \(3{x^2} + x + 5 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình vô nghiệm.
b) Tam thức \(f(x) = - 3{x^2} + 2\sqrt 3 x - 1\) có \(\Delta ' = 0\), hệ số a = -3 < 0 nên f(x) có nghiệm kép \(x = \frac{{\sqrt 3 }}{3}\) và f(x) luôn âm (cùng dấu với a) với mọi \(x \ne \frac{{\sqrt 3 }}{3}\), tức là \( - 3{x^2} + 2\sqrt 3 x - 1 < 0\) với mọi \(x \ne \frac{{\sqrt 3 }}{3}\).
Suy ra bất phương trình có nghiệm duy nhất \(x = \frac{{\sqrt 3 }}{3}\).
c) Tam thức \(f(x) = - {x^2} + 2x + 1\) có \(\Delta ' = 2 > 0\) nên f(x) có hai nghiệm \({x_1} = 1 - \sqrt 2 \) và \({x_2} = 1 + \sqrt 2 \).
Mặt khác, a = -1 < 0, do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là \(S = \left( {1 - \sqrt 2 ;1 + \sqrt 2 } \right)\).
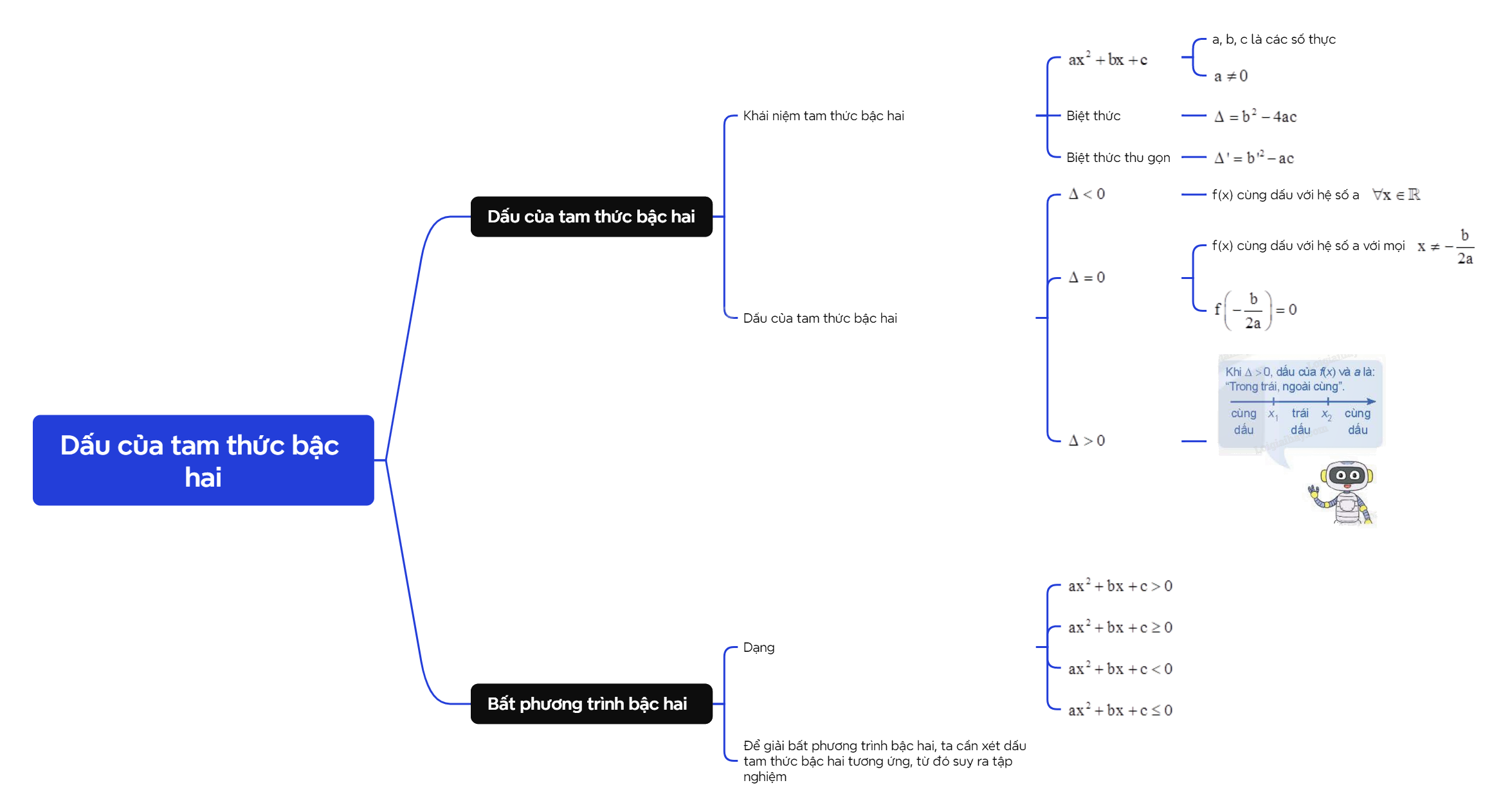
Tam thức bậc hai là một biểu thức đại số có dạng f(x) = ax2 + bx + c, trong đó a, b, c là các số thực và a ≠ 0. Việc xác định dấu của tam thức bậc hai là một kỹ năng quan trọng trong toán học, đặc biệt là khi giải các bài toán liên quan đến bất phương trình bậc hai.
Dấu của tam thức bậc hai phụ thuộc vào hệ số a và biệt thức Δ = b2 - 4ac. Có ba trường hợp xảy ra:
Để xác định dấu của tam thức bậc hai, ta có thể sử dụng sơ đồ dấu. Sơ đồ dấu là một công cụ trực quan giúp ta xác định khoảng giá trị của x mà tam thức bậc hai dương, âm hoặc bằng không.
Ví dụ: Xét tam thức bậc hai f(x) = 2x2 - 5x + 2. Ta có:
Vậy tam thức bậc hai có hai nghiệm phân biệt. Ta tìm nghiệm bằng cách giải phương trình 2x2 - 5x + 2 = 0. Nghiệm là x1 = 1/2 và x2 = 2.
Sử dụng sơ đồ dấu, ta có:
| x | x < 1/2 | 1/2 < x < 2 | x > 2 |
|---|---|---|---|
| 2x2 - 5x + 2 | + | - | + |
Lý thuyết dấu của tam thức bậc hai có nhiều ứng dụng trong toán học, đặc biệt là trong việc giải các bài toán sau:
Để củng cố kiến thức về lý thuyết dấu của tam thức bậc hai, bạn có thể thực hành giải các bài tập sau:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết dấu của tam thức bậc hai. Chúc bạn học tốt!