Hàm số bậc hai là một trong những chủ đề quan trọng bậc nhất trong chương trình Toán 10 Kết nối tri thức. Việc nắm vững lý thuyết và các ứng dụng của hàm số bậc hai không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng vững chắc cho các kiến thức toán học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, chi tiết và dễ hiểu về lý thuyết Hàm số bậc hai, giúp bạn tự tin chinh phục môn Toán.
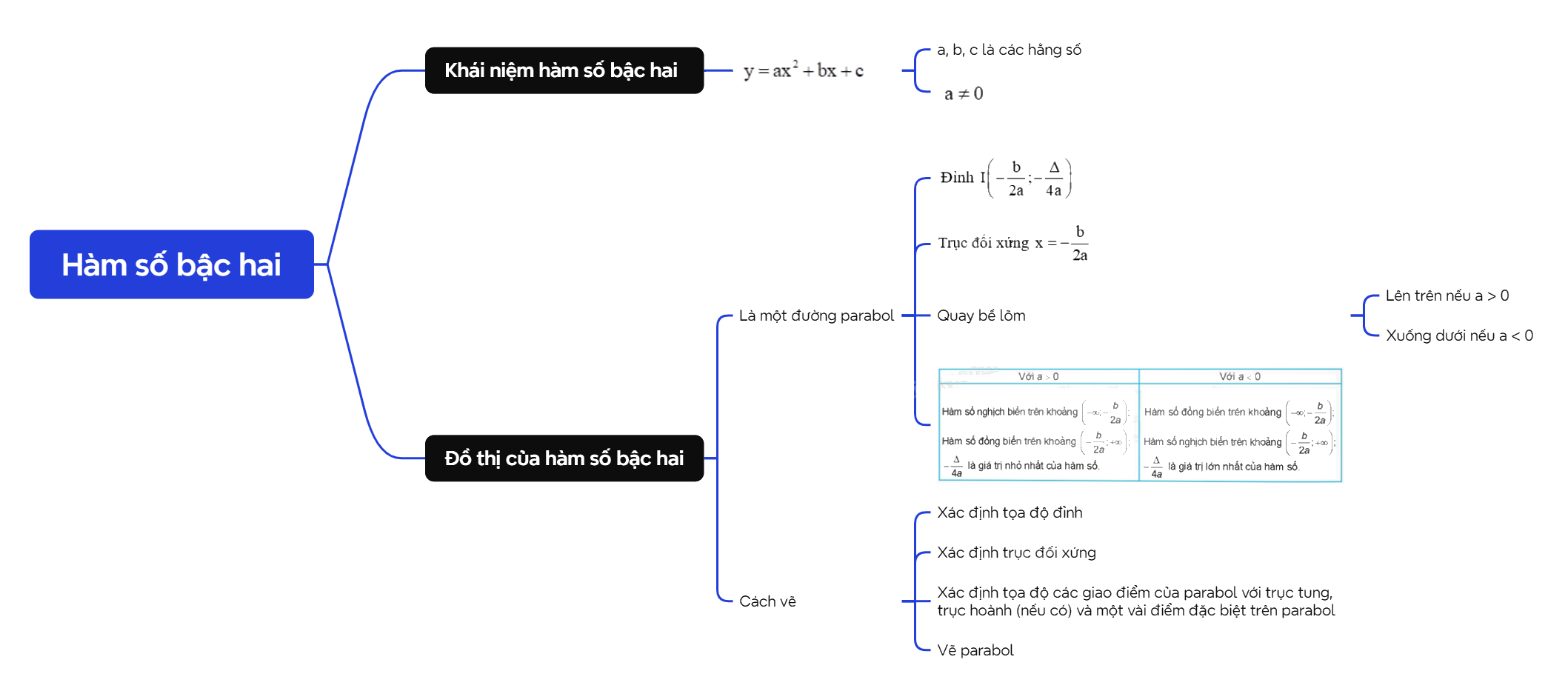
A. Lý thuyết 1. Khái niệm hàm số bậc hai
A. Lý thuyết
1. Khái niệm hàm số bậc hai
Hàm số bậc hai là hàm số cho bởi công thức \(y = a{x^2} + bx + c\), trong đó x là biến số, a, b, c là các hằng số và \(a \ne 0\). Tập xác định của hàm số bậc hai là \(\mathbb{R}\). |
Nhận xét: Hàm số \(y = a{x^2}\) \((a \ne 0)\) đã học ở lớp 9 là một trường hợp đặc biệt của hàm số bậc hai với b = c = 0.
2. Đồ thị của hàm số bậc hai
Hàm số bậc hai \(y = a{x^2} + bx + c\) \((a \ne 0)\) có đồ thị là một đường parabol có đỉnh là điểm \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\), có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}}\). Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0. Để vẽ đường parabol \(y = a{x^2} + bx + c\) ta tiến hành theo các bước sau: 1. Xác định tọa độ đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\). 2. Xác định trục đối xứng \(x = - \frac{b}{{2a}}\). 3. Xác định tọa độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol. 4. Vẽ parabol. |
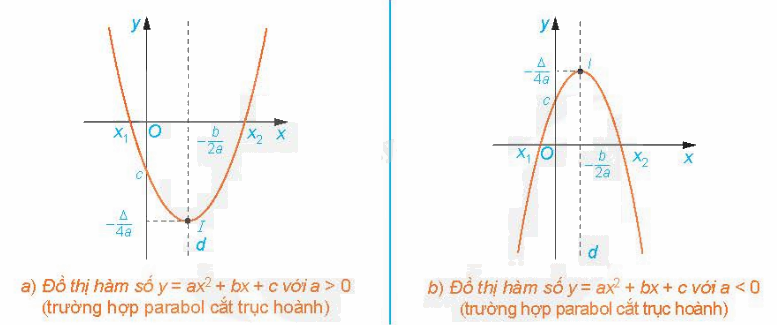
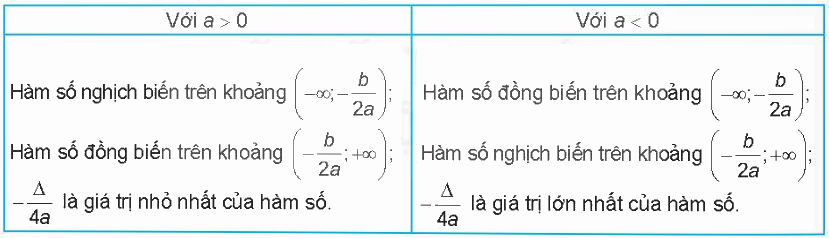
Nhận xét: Từ đồ thị hàm số \(y = a{x^2} + bx + c\) \((a \ne 0)\), ta suy ra tính chất của hàm số \(y = a{x^2} + bx + c\) \((a \ne 0)\):
B. Bài tập
Bài 1: Hàm số nào dưới đây là hàm số bậc hai?
A. \(y = {x^2} + 3{x^2} + 2\)
B. \(y = \frac{1}{{{x^2}}}\)
C. \(y = - 3{x^2} + 1\)
D. \(y = 3{\left( {\frac{1}{x}} \right)^2} - 3\frac{1}{x} - 1\)
Giải:
Hàm số \(y = - 3{x^2} + 1\) là hàm số bậc hai với a = -3, b = 0, c = 1. Hàm số thỏa mãn điều kiện \(a \ne 0\) \(( - 3 \ne 0)\) và có tập xác định là \(\mathbb{R}\).
Bài 2:
a) Vẽ parabol \(y = - 2{x^2} - 2x + 4\).
b) Từ đồ thị, hãy tìm khoảng đồng biến, nghịch biến và giá trị lớn nhất của hàm số \(y = - 2{x^2} - 2x + 4\).
Giải:
a) Ta có a = -2 < 0 nên parabol quay bề lõm xuống dưới.
Đỉnh \(I\left( { - \frac{1}{2};\frac{9}{2}} \right)\). Trục đối xứng \(x = - \frac{1}{2}\). Giao điểm của đồ thị với trục Oy là A(0;4). Parabol cắt trục hoành tại điểm có hoành độ là nghiệm của phương trình \( - 2{x^2} - 2x + 4 = 0\), tức là x = 1 và x = -2.
Để vẽ đồ thị chính xác hơn, ta có thể lấy thêm điểm đối xứng vói A qua trục đối xứng \(x = - \frac{1}{2}\) là B(-1;4).
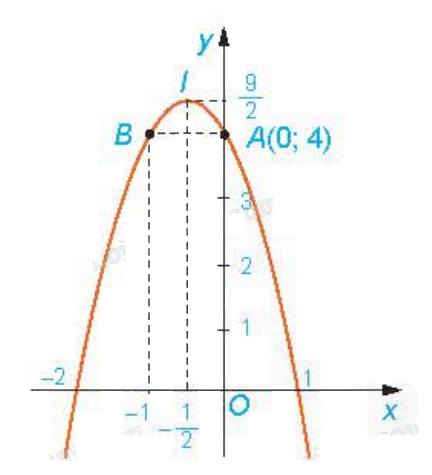
b) Từ đồ thị ta thấy:
Hàm số \(y = - 2{x^2} - 2x + 4\) đồng biến trên \(\left( { - \infty ; - \frac{1}{2}} \right)\), nghịch biến trên \(\left( { - \frac{1}{2}; + \infty } \right)\).
Giá trị lớn nhất của hàm số là \(y = \frac{9}{2}\) khi \(x = - \frac{1}{2}\).
Hàm số bậc hai là một trong những khái niệm cơ bản và quan trọng trong đại số, đặc biệt là trong chương trình Toán 10 Kết nối tri thức. Hiểu rõ về hàm số bậc hai giúp học sinh giải quyết nhiều bài toán thực tế và là nền tảng cho các kiến thức toán học nâng cao hơn.
Hàm số bậc hai có dạng tổng quát: y = ax2 + bx + c, trong đó a, b, c là các số thực và a ≠ 0. 'a' được gọi là hệ số bậc hai, 'b' là hệ số bậc nhất và 'c' là hệ số tự do.
Tập xác định của hàm số bậc hai là tập hợp tất cả các số thực, ký hiệu là ℝ. Điều này có nghĩa là hàm số bậc hai có thể nhận bất kỳ giá trị nào của x.
Đồ thị của hàm số bậc hai là một đường cong được gọi là parabol. Hình dạng của parabol phụ thuộc vào dấu của hệ số 'a':
Đỉnh của parabol là điểm thấp nhất (nếu a > 0) hoặc điểm cao nhất (nếu a < 0) trên đồ thị. Tọa độ đỉnh của parabol được tính như sau:
I(xI; yI), với:
Trục đối xứng của parabol là đường thẳng đi qua đỉnh và song song với trục Oy. Phương trình của trục đối xứng là: x = -b / 2a.
Bảng biến thiên giúp ta hình dung được sự thay đổi của hàm số khi x thay đổi. Việc lập bảng biến thiên bao gồm các bước sau:
Đồ thị hàm số bậc hai bị ảnh hưởng bởi các yếu tố sau:
Hàm số bậc hai có nhiều ứng dụng trong thực tế, ví dụ như:
Ví dụ 1: Xác định hệ số a, b, c của hàm số y = 2x2 - 5x + 3.
Giải: a = 2, b = -5, c = 3.
Ví dụ 2: Tìm tọa độ đỉnh của parabol y = x2 - 4x + 1.
Giải: xI = -(-4) / (2 * 1) = 2; yI = -( (-4)2 - 4 * 1 * 1) / (4 * 1) = -(-12) / 4 = 3. Vậy đỉnh của parabol là I(2; 3).
Để nắm vững lý thuyết hàm số bậc hai, bạn nên luyện tập thường xuyên các bài tập trong sách giáo khoa và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp hệ thống bài tập đa dạng, phong phú với các mức độ khó khác nhau, giúp bạn củng cố kiến thức và nâng cao kỹ năng giải toán.
Hy vọng với những kiến thức được trình bày trên, bạn đã có cái nhìn tổng quan và hiểu rõ hơn về lý thuyết hàm số bậc hai - SGK Toán 10 Kết nối tri thức. Chúc bạn học tập tốt!