Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 2 Kết nối tri thức. Mục 2 trang 22, 23 tập trung vào các kiến thức quan trọng về vectơ, phép toán vectơ và ứng dụng của chúng trong hình học.
Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giaitoan.edu.vn đã biên soạn bộ giải bài tập này với mục đích giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập một cách hiệu quả.
Trở lại tình huống mở đầu. Với yêu cầu mảnh đất được rào chắn có diện tích không nhỏ hơn 48 ({m^2}), hãy viết bất đẳng thức thể hiện sự so sánh biểu thức tính diện tích Độ cao so với mặt đất của một quá bóng được ném lên theo phương thẳng đứng được mô tả bởi hàm số bậc hai
Trở lại tình huống mở đầu. Với yêu cầu mảnh đất được rào chắn có diện tích không nhỏ hơn 48 \({m^2}\), hãy viết bất đẳng thức thể hiện sự so sánh biểu thức tính diện tích \(S(x) = - 2{x^2} + 20x\) với 48
Lời giải chi tiết:
Để diện tích của mảnh vườn không nhỏ hơn 48 \({m^2}\)thì
\(S(x) \ge 48 \Rightarrow - 2{x^2} + 20x \ge 48 \Leftrightarrow - 2{x^2} + 20x - 48 \ge 0\)
Giải các bất phương trình sau:
a) \( - 5{x^2} + x - 1 \le 0\)
b) \({x^2} - 8x + 16 \le 0\)
c) \({x^2} - x + 6 > 0\)
Phương pháp giải:
Để giải bất phương trình bậc hai, ta cần xét dấu tam thức \(f(x) = a{x^2} + bx + x(a \ne 0)\)
từ đó suy ra tập nghiệm.
Xét dấu tam thức bậc hai \(f(x) = a{x^2} + bx + c\)
Bước 1: Tính \(\Delta = {b^2} - 4ac\)
Bước 2:
- Nếu \(\Delta < 0\) thì \(f(x)\) luôn cùng dấu với a với mọi \(x \in \mathbb{R}\)
- Nếu \(\Delta = 0\) thì \(f(x)\)có nghiệm kép là \({x_0}\) . Vậy \(f(x)\)cùng dấu với a với \(x \ne {x_0}\)
- Nếu \(\Delta > 0\) thì \(f(x)\)có 2 nghiệm là \({x_1};{x_2}\)\(({x_1} < {x_2})\). Ta lập bảng xét dấu.

Lời giải chi tiết:
a) Tam thức \(f(x) = - 5{x^2} + x - 1\) có \(\Delta = - 19 < 0\), hệ số \(a = - 5 < 0\) nên f(x) luôn âm (cùng dấu với a) với mọi x, tức là \(\)\( - 5{x^2} + x - 1 < 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm
b) Tam thức \(g(x) = {x^2} - 8x + 16\) có \(\Delta = 0\), hệ số a=1>0 nên g(x) luôn dương (cùng dấu với a) với mọi \(x \ne 4\), tức là \({x^2} - 8x + 16 > 0\) với mọi \(x \ne 4\)
Suy ra bất phương trình có nghiệm duy nhất là x=4
c) Tam thức \(h(x) = {x^2} - x + 6\) có \(\Delta = - 2 < 0\), hệ số a=1>0 nên h(x) luôn dương (cùng dấu với a) với mọi x, tức là \({x^2} - x + 6 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm
Độ cao so với mặt đất của một quá bóng được ném lên theo phương thẳng đứng được mô tả bởi hàm số bậc hai \(h(t) = - 4,9{t^2} + 20t + 1\), ở độ cao \(h(t)\)tính bằng mét và thời gian t tình bằng giây. Trong khoảng thời điểm nào trong quá trình bay của nó, quả bóng sẽ ở độ cao trên 5m so với mặt đất.
Phương pháp giải:
Tìm khoảng thời gian t để \(h(t) > 5\), bài toán đưa về xét dấu tam thức \(f(t) = h(t) - 5\)
Các bước xét dấu tam thức bậc hai \(f(t) = a{t^2} + bt + c\)
Bước 1: Tính \(\Delta = {b^2} - 4ac\)
Bước 2:
- Nếu \(\Delta < 0\) thì \(f(t)\) luôn cùng dấu với a với mọi \(t \in \mathbb{R}\)
- Nếu \(\Delta = 0\) thì \(f(t)\)có nghiệm kép là \({t_0}\) . Vậy \(f(t)\)cùng dấu với a với \(t \ne {t_0}\)
- Nếu \(\Delta > 0\) thì \(f(t)\)có 2 nghiệm là \({t_1};{t_2}\)\(({t_1} < {t_2})\). Ta lập bảng xét dấu.

Kết luận khoảng chứa t thỏa mãn \(f(t) > 0\)
Lời giải chi tiết:
Để quả bóng ở độ cao trên 5m so với mặt đất thì:
\(\begin{array}{l}h(t) > 5\\ \Rightarrow - 4,9{t^2} + 20t + 1 > 5\\ \Rightarrow - 4,9{t^2} + 20t - 4 > 0\end{array}\)
Đặt \(f(t) = - 4,9{t^2} + 20t - 4\)có \(\Delta ' = b{'^2} - ac = {10^2} - ( - 4,9).( - 4) = 80,4 > 0\)nên \(f(t)\)có 2 nghiệm: \(\begin{array}{l}{t_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a} = \frac{{ - 10 + \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 - \sqrt {80,4} }}{{4,9}}\\{t_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a} = \frac{{ - 10 - \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 + \sqrt {80,4} }}{{4,9}}\end{array}\)
Mặt khác \(a = - 4,9 < 0\), do đó ta có bảng xét dấu sau
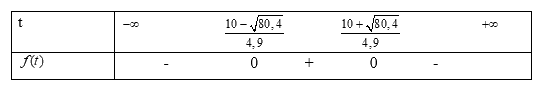
Do đó để \(h(t) > 5\)thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)
Vậy để quả bóng sẽ ở độ cao trên 5m so với mặt đất thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)
Trở lại tình huống mở đầu. Với yêu cầu mảnh đất được rào chắn có diện tích không nhỏ hơn 48 \({m^2}\), hãy viết bất đẳng thức thể hiện sự so sánh biểu thức tính diện tích \(S(x) = - 2{x^2} + 20x\) với 48
Lời giải chi tiết:
Để diện tích của mảnh vườn không nhỏ hơn 48 \({m^2}\)thì
\(S(x) \ge 48 \Rightarrow - 2{x^2} + 20x \ge 48 \Leftrightarrow - 2{x^2} + 20x - 48 \ge 0\)
Giải các bất phương trình sau:
a) \( - 5{x^2} + x - 1 \le 0\)
b) \({x^2} - 8x + 16 \le 0\)
c) \({x^2} - x + 6 > 0\)
Phương pháp giải:
Để giải bất phương trình bậc hai, ta cần xét dấu tam thức \(f(x) = a{x^2} + bx + x(a \ne 0)\)
từ đó suy ra tập nghiệm.
Xét dấu tam thức bậc hai \(f(x) = a{x^2} + bx + c\)
Bước 1: Tính \(\Delta = {b^2} - 4ac\)
Bước 2:
- Nếu \(\Delta < 0\) thì \(f(x)\) luôn cùng dấu với a với mọi \(x \in \mathbb{R}\)
- Nếu \(\Delta = 0\) thì \(f(x)\)có nghiệm kép là \({x_0}\) . Vậy \(f(x)\)cùng dấu với a với \(x \ne {x_0}\)
- Nếu \(\Delta > 0\) thì \(f(x)\)có 2 nghiệm là \({x_1};{x_2}\)\(({x_1} < {x_2})\). Ta lập bảng xét dấu.

Lời giải chi tiết:
a) Tam thức \(f(x) = - 5{x^2} + x - 1\) có \(\Delta = - 19 < 0\), hệ số \(a = - 5 < 0\) nên f(x) luôn âm (cùng dấu với a) với mọi x, tức là \(\)\( - 5{x^2} + x - 1 < 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm
b) Tam thức \(g(x) = {x^2} - 8x + 16\) có \(\Delta = 0\), hệ số a=1>0 nên g(x) luôn dương (cùng dấu với a) với mọi \(x \ne 4\), tức là \({x^2} - 8x + 16 > 0\) với mọi \(x \ne 4\)
Suy ra bất phương trình có nghiệm duy nhất là x=4
c) Tam thức \(h(x) = {x^2} - x + 6\) có \(\Delta = - 2 < 0\), hệ số a=1>0 nên h(x) luôn dương (cùng dấu với a) với mọi x, tức là \({x^2} - x + 6 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm
Độ cao so với mặt đất của một quá bóng được ném lên theo phương thẳng đứng được mô tả bởi hàm số bậc hai \(h(t) = - 4,9{t^2} + 20t + 1\), ở độ cao \(h(t)\)tính bằng mét và thời gian t tình bằng giây. Trong khoảng thời điểm nào trong quá trình bay của nó, quả bóng sẽ ở độ cao trên 5m so với mặt đất.
Phương pháp giải:
Tìm khoảng thời gian t để \(h(t) > 5\), bài toán đưa về xét dấu tam thức \(f(t) = h(t) - 5\)
Các bước xét dấu tam thức bậc hai \(f(t) = a{t^2} + bt + c\)
Bước 1: Tính \(\Delta = {b^2} - 4ac\)
Bước 2:
- Nếu \(\Delta < 0\) thì \(f(t)\) luôn cùng dấu với a với mọi \(t \in \mathbb{R}\)
- Nếu \(\Delta = 0\) thì \(f(t)\)có nghiệm kép là \({t_0}\) . Vậy \(f(t)\)cùng dấu với a với \(t \ne {t_0}\)
- Nếu \(\Delta > 0\) thì \(f(t)\)có 2 nghiệm là \({t_1};{t_2}\)\(({t_1} < {t_2})\). Ta lập bảng xét dấu.

Kết luận khoảng chứa t thỏa mãn \(f(t) > 0\)
Lời giải chi tiết:
Để quả bóng ở độ cao trên 5m so với mặt đất thì:
\(\begin{array}{l}h(t) > 5\\ \Rightarrow - 4,9{t^2} + 20t + 1 > 5\\ \Rightarrow - 4,9{t^2} + 20t - 4 > 0\end{array}\)
Đặt \(f(t) = - 4,9{t^2} + 20t - 4\)có \(\Delta ' = b{'^2} - ac = {10^2} - ( - 4,9).( - 4) = 80,4 > 0\)nên \(f(t)\)có 2 nghiệm: \(\begin{array}{l}{t_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a} = \frac{{ - 10 + \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 - \sqrt {80,4} }}{{4,9}}\\{t_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a} = \frac{{ - 10 - \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 + \sqrt {80,4} }}{{4,9}}\end{array}\)
Mặt khác \(a = - 4,9 < 0\), do đó ta có bảng xét dấu sau
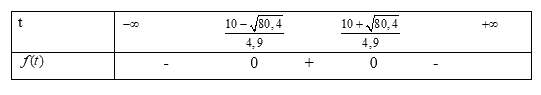
Do đó để \(h(t) > 5\)thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)
Vậy để quả bóng sẽ ở độ cao trên 5m so với mặt đất thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)
Mục 2 của SGK Toán 10 tập 2 Kết nối tri thức tập trung vào việc củng cố kiến thức về vectơ, bao gồm các khái niệm cơ bản, các phép toán trên vectơ (cộng, trừ, nhân với một số thực) và ứng dụng của vectơ trong việc giải quyết các bài toán hình học.
Lời giải: Để tìm vectơ a + b, ta sử dụng quy tắc hình bình hành. Vẽ hình bình hành ABCD sao cho AB = a và AD = b. Khi đó, vectơ AC là vectơ tổng a + b. Tương tự, để tìm vectơ a - b, ta sử dụng quy tắc trừ vectơ. Vectơ CB là vectơ hiệu a - b.
Lời giải: Vectơ ka là vectơ có cùng hướng với vectơ a nếu k > 0 và ngược hướng với vectơ a nếu k < 0. Độ dài của vectơ ka là |k| lần độ dài của vectơ a.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải các bài tập về vectơ trong SGK Toán 10 tập 2 Kết nối tri thức. Chúc các em học tập tốt!