Lý thuyết Mệnh đề là một phần quan trọng trong chương trình Toán học, đặc biệt là trong Logic học. Nó cung cấp các công cụ cơ bản để phân tích và suy luận logic, giúp bạn hiểu rõ hơn về các mối quan hệ giữa các phát biểu và xây dựng các lập luận chặt chẽ.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu về Lý thuyết Mệnh đề, cùng với các bài tập thực hành đa dạng để bạn có thể nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.
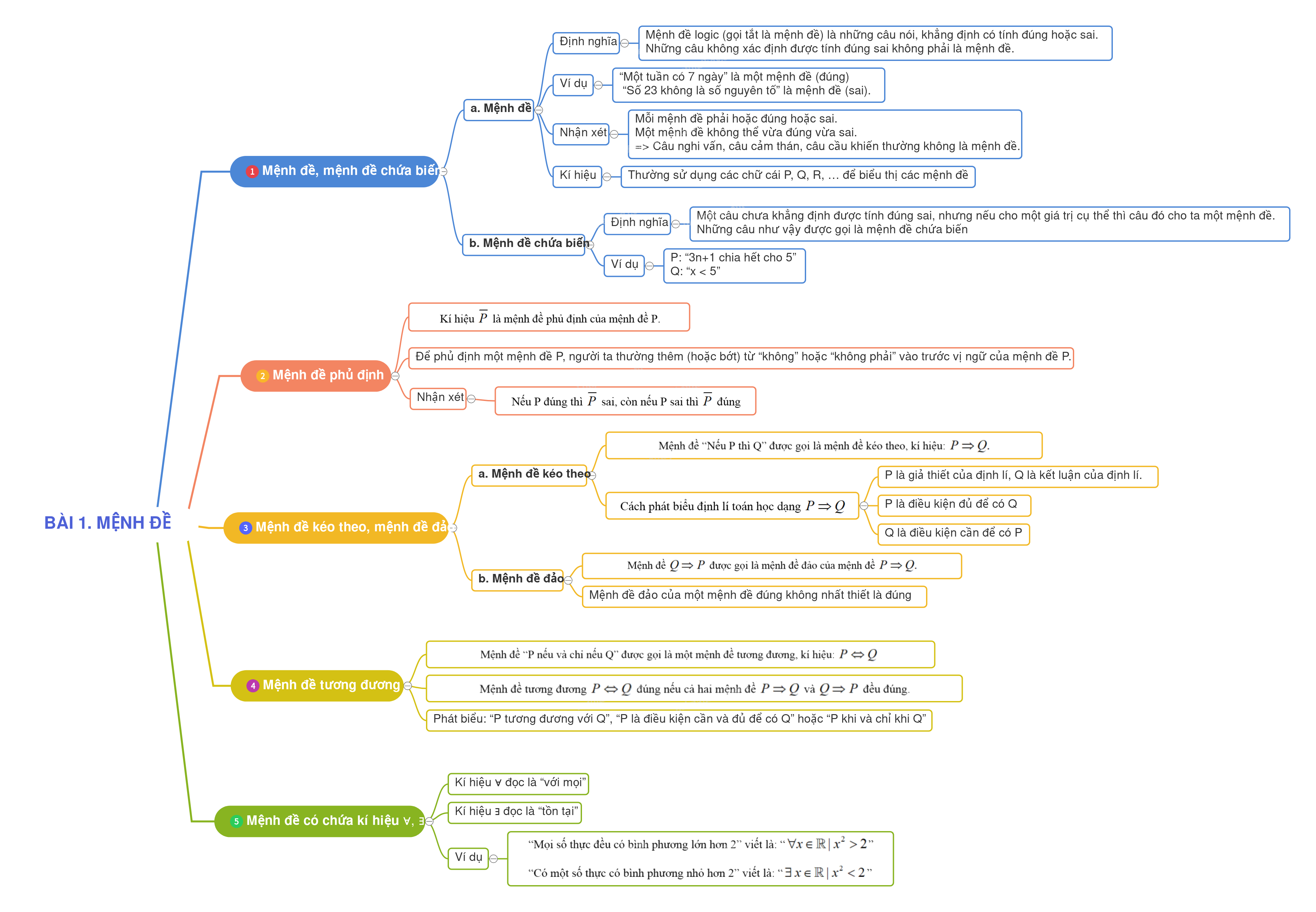
1. Mệnh đề, mệnh đề chứa biến
1. Mệnh đề, mệnh đề chứa biến
a. Mệnh đề
Định nghĩa:
Mệnh đề logic (gọi tắt là mệnh đề) là những câu nói, khẳng định có tính đúng hoặc sai.
Những câu không xác định được tính đúng sai không phải là mệnh đề.
Ví dụ: “Một tuần có 7 ngày” là một mệnh đề (đúng)
“Số 23 không là số nguyên tố” là mệnh đề (sai).
Nhận xét:
Mỗi mệnh đề phải hoặc đúng hoặc sai.
Một mệnh đề không thể vừa đúng vừa sai.
=> Câu nghi vấn, câu cảm thán, câu cầu khiến thường không là mệnh đề.
Kí hiệu: Thường sử dụng các chữ cái P, Q, R, … để biểu thị các mệnh đề.
b. Mệnh đề chứa biến
Một câu chưa khẳng định được tính đúng sai, nhưng nếu cho một giá trị cụ thể thì câu đó cho ta một mệnh đề. Những câu như vậy được gọi là mệnh đề chứa biến.
Ví dụ: P: “3n+1 chia hết cho 5”
Q: “x < 5”
2. Mệnh đề phủ định
+ Để phủ định một mệnh đề P, người ta thường thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề P. Kí hiệu \(\overline P \) là mệnh đề phủ định của mệnh đề P.
Nhận xét:
+ Nếu P đúng thì \(\overline P \) sai, còn nếu P sai thì \(\overline P \) đúng.
3. Mệnh đề kéo theo, mệnh đề đảo
a. Mệnh đề kéo theo
+ Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, kí hiệu: \(P \Rightarrow Q.\)
+ Cách phát biểu định lí toán học dạng \(P \Rightarrow Q\):
P là giả thiết của định lí, Q là kết luận của định lí.
P là điều kiện đủ để có Q
Q là điều kiện cần để có P.
b. Mệnh đề đảo
Mệnh đề \(Q \Rightarrow P\) được gọi là mệnh đề đảo của mệnh đề \(P \Rightarrow Q.\)
Chú ý: Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.
4. Mệnh đề tương đương
+ Mệnh đề “P nếu và chỉ nếu Q” được gọi là một mệnh đề tương đương, kí hiệu: \(P \Leftrightarrow Q\)
+ Mệnh đề tương đương \(P \Leftrightarrow Q\) đúng nếu cả hai mệnh đề \(P \Rightarrow Q\) và \(Q \Rightarrow P\) đều đúng.
+ Phát biểu: “P tương đương với Q”, “P là điều kiện cần và đủ để có Q” hoặc “P khi và chỉ khi Q”.
5. Mệnh đề có chứa kí hiệu \(\forall ,\exists \)
Kí hiệu \(\forall \) đọc là “với mọi”.
Kí hiệu \(\exists \) đọc là “tồn tại”.
Ví dụ:
“Mọi số thực đều có bình phương lớn hơn 2” viết là: “\(\forall x \in \mathbb{R}|{x^2} > 2\)”
“Có một số thực có bình phương nhỏ hơn 2” viết là: “\(\exists \;x \in \mathbb{R}|{x^2} < 2\)”
Lý thuyết Mệnh đề, hay còn gọi là Logic Mệnh đề, là một nhánh của logic toán học nghiên cứu về các mệnh đề và mối quan hệ logic giữa chúng. Đây là nền tảng cơ bản cho việc xây dựng các hệ thống suy luận và chứng minh trong toán học và khoa học máy tính.
Một mệnh đề là một câu khẳng định có thể xác định được tính đúng sai của nó. Mệnh đề có thể đúng hoặc sai, nhưng không thể vừa đúng vừa sai. Ví dụ:
Trong Lý thuyết Mệnh đề, chúng ta sử dụng các phép toán logic để kết hợp các mệnh đề đơn giản thành các mệnh đề phức tạp hơn. Các phép toán logic cơ bản bao gồm:
Bảng chân trị là một công cụ quan trọng để xác định giá trị chân lý của các mệnh đề phức tạp dựa trên giá trị chân lý của các mệnh đề đơn giản thành phần. Dưới đây là bảng chân trị của các phép toán logic cơ bản:
| P | Q | ¬P | P ∧ Q | P ∨ Q | P → Q | P ↔ Q |
|---|---|---|---|---|---|---|
| Đ | Đ | S | Đ | Đ | Đ | Đ |
| Đ | S | S | S | Đ | S | S |
| S | Đ | Đ | S | Đ | Đ | S |
| S | S | Đ | S | S | Đ | Đ |
Có một số định luật logic quan trọng giúp chúng ta đơn giản hóa và biến đổi các biểu thức logic:
Lý thuyết Mệnh đề có nhiều ứng dụng trong các lĩnh vực khác nhau:
Để củng cố kiến thức về Lý thuyết Mệnh đề, bạn có thể thực hành giải các bài tập sau:
Lý thuyết Mệnh đề là một công cụ mạnh mẽ giúp bạn suy nghĩ logic và giải quyết các vấn đề một cách hiệu quả. Hãy dành thời gian để học và thực hành để nắm vững kiến thức này!