Phương trình đường thẳng là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán 10 Kết nối tri thức. Việc nắm vững lý thuyết này không chỉ giúp bạn giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về lý thuyết Phương trình đường thẳng, kèm theo các ví dụ minh họa và bài tập vận dụng đa dạng.
A. Lý thuyết 1. Phương trình tổng quát của đường thẳng a) Vecto pháp tuyến của đường thẳng
A. Lý thuyết
1. Phương trình tổng quát của đường thẳng
a) Vecto pháp tuyến của đường thẳng
| Vecto \(\overrightarrow n \) được gọi là vecto pháp tuyến của đường thẳng \(\Delta \) nếu \(\overrightarrow n \ne \overrightarrow 0 \) và giá của vecto \(\overrightarrow n \) vuông góc với \(\Delta \). |
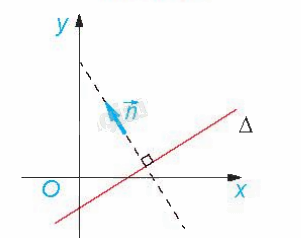
Nhận xét:
- Nếu \(\overrightarrow n \) là một vecto pháp tuyến của \(\Delta \) thì \(k\overrightarrow n \) \((k \ne 0)\) cũng là một vecto pháp tuyến của \(\Delta \).
- Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vecto pháp tuyến của đường thẳng đó.
b) Phương trình tổng quát của đường thẳng
| Trong mặt phẳng tọa độ, mọi đường thẳng đều có phương trình tổng quát dạng \(ax + by + c = 0\) (a và b không đồng thời bằng 0). Ngược lại, mỗi phương trình dạng \(ax + by + c = 0\) (a và b không đồng thời bằng 0) đều là phương trình của một đường thẳng, nhận \(\overrightarrow n (a;b)\) là một vecto pháp tuyến. |
2. Phương trình tham số của đường thẳng
a) Vecto chỉ phương của đường thẳng
| Vecto \(\overrightarrow u \) được gọi là vecto chỉ phương của đường thẳng \(\Delta \) nếu \(\overrightarrow u \ne \overrightarrow 0 \) và giá của vecto \(\overrightarrow u \) song song hoặc trùng với \(\Delta \). |
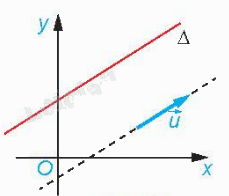
Nhận xét:
- Nếu \(\overrightarrow u \) là một vecto chỉ phương của \(\Delta \) thì \(k\overrightarrow u \) \((k \ne 0)\) cũng là một vecto chỉ phương của \(\Delta \).
- Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vecto chỉ phương của đường thẳng đó.
b) Phương trình tham số của đường thẳng
Cho đường thẳng \(\Delta \) đi qua điểm \(A({x_0};{y_0})\) và có vecto chỉ phương \(\overrightarrow u (a;b)\). Khi đó, điểm M(x;y) thuộc đường thẳng \(\Delta \) khi và chỉ khi tồn tại số thực t sao cho \(\overrightarrow {AM} = t\overrightarrow u \), hay \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\). Hệ trên được gọi là phương trình tham số của đường thẳng \(\Delta \). |
B. Bài tập
Lập phương trình đường thẳng \(\Delta \) thỏa mãn:
a) Đi qua M(-2;-3) và có \(\overrightarrow n = (2;5)\) là vecto pháp tuyến.
b) Đi qua M(3;-5) và có \(\overrightarrow u = (2; - 4)\) là vecto chỉ phương.
c) Đi qua A(-3;4) và B(1;-1).
Giải:
a) Phương trình \(\Delta \) là \(2(x + 2) + 5(y + 3) = 0 \Leftrightarrow 2x + 5y + 19 = 0\).
b) Phương trình \(\Delta \) là \(\frac{{x - 3}}{2} = \frac{{y + 5}}{{ - 4}} \Leftrightarrow 4x + 2y - 2 = 0 \Leftrightarrow 2x + y - 1 = 0\).
c) Phương trình \(\Delta \) là \(\frac{{x + 3}}{{1 - ( - 3)}} = \frac{{y - 4}}{{ - 1 - 4}} \Leftrightarrow \frac{{x + 3}}{4} = \frac{{y - 4}}{{ - 5}} \Leftrightarrow 5x + 4y - 1 = 0\).
Phương trình đường thẳng là một biểu thức toán học mô tả một đường thẳng trên mặt phẳng tọa độ. Nó đóng vai trò quan trọng trong việc giải quyết nhiều bài toán hình học và đại số. Trong chương trình Toán 10 Kết nối tri thức, học sinh sẽ được làm quen với các dạng phương trình đường thẳng khác nhau và cách ứng dụng chúng vào giải quyết các bài toán thực tế.
Có ba dạng phương trình đường thẳng phổ biến:
Hệ số góc (m) của đường thẳng y = mx + b thể hiện độ dốc của đường thẳng. Nếu m > 0, đường thẳng đi lên từ trái sang phải. Nếu m < 0, đường thẳng đi xuống từ trái sang phải. Nếu m = 0, đường thẳng là đường thẳng ngang.
Có thể chuyển đổi giữa các dạng phương trình đường thẳng khác nhau. Ví dụ:
Cho hai đường thẳng có phương trình:
Khi đó:
Bài 1: Viết phương trình đường thẳng đi qua điểm A(1; 2) và có hệ số góc m = 3.
Giải: Phương trình đường thẳng có dạng y = mx + b. Thay điểm A(1; 2) và m = 3 vào, ta có: 2 = 3(1) + b => b = -1. Vậy phương trình đường thẳng là y = 3x - 1.
Bài 2: Tìm phương trình tổng quát của đường thẳng đi qua hai điểm B(0; -1) và C(2; 1).
Giải: Hệ số góc m = (1 - (-1))/(2 - 0) = 1. Phương trình đường thẳng có dạng y = x + b. Thay điểm B(0; -1) vào, ta có: -1 = 0 + b => b = -1. Vậy phương trình đường thẳng là y = x - 1. Chuyển về dạng tổng quát: x - y - 1 = 0.
Phương trình đường thẳng được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Việc hiểu rõ lý thuyết và các ứng dụng của phương trình đường thẳng là rất quan trọng đối với học sinh lớp 10. Hãy luyện tập thường xuyên để nắm vững kiến thức này và áp dụng vào giải quyết các bài toán thực tế.