Lý thuyết tập hợp là một trong những nền tảng cơ bản của toán học, đóng vai trò quan trọng trong nhiều lĩnh vực khác nhau.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu về lý thuyết tập hợp và các phép toán trên tập hợp, giúp bạn nắm vững kiến thức một cách nhanh chóng và hiệu quả.
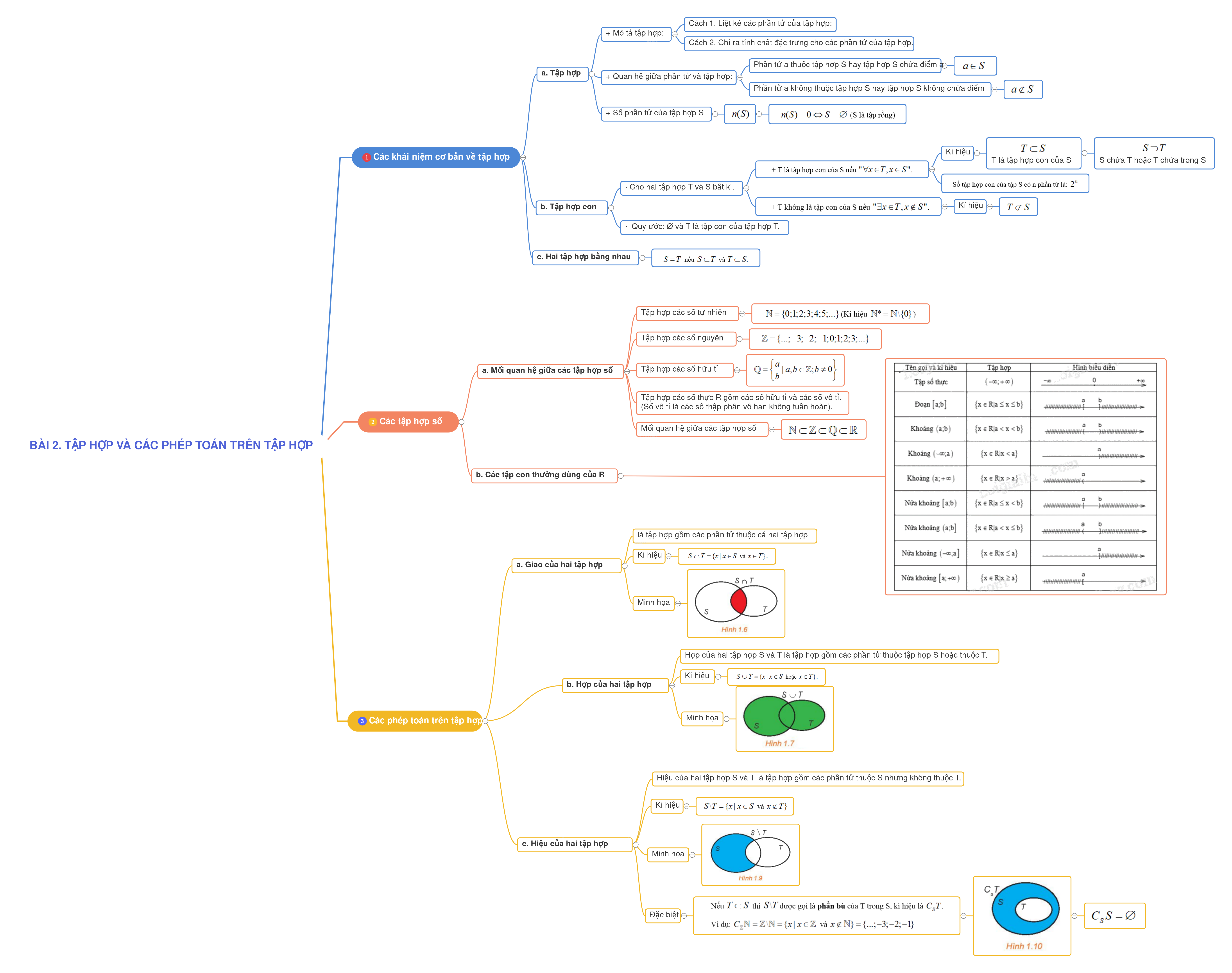
1. Các khái niệm cơ bản về tập hợp
a. Tập hợp
+ Mô tả tập hợp:
Cách 1. Liệt kê các phần tử của tập hợp;
Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
+ Quan hệ giữa phần tử và tập hợp:
Phần tử a thuộc tập hợp S hay tập hợp S chứa điểm a: \(a \in S\)
Phần tử a không thuộc tập hợp S hay tập hợp S không chứa điểm a: \(a \notin S\)
+ Số phần tử của tập hợp S: \(n(S)\)
\(n(S) = 0 \Leftrightarrow S = \emptyset \) (S là tập rỗng)
b. Tập hợp con
+ T là tập hợp con của S nếu
Kí hiệu: \(T \subset S\)(T là tập hợp con của S) hoặc \(S \supset T\)(S chứa T hoặc T chứa trong S)
Số tập hợp con của tập S có n phần tử là: \({2^n}\)
+ T không là tập con của S nếu
Kí hiệu: \(T \not\subset S\)
c. Hai tập hợp bằng nhau
\(S = T\) nếu \(S \subset T\) và \(T \subset S.\)
2. Các tập hợp số
a. Mối quan hệ giữa các tập hợp số
Tập hợp các số tự nhiên \(\mathbb{N} = \{ 0;1;2;3;4;5;...\} \)(Kí hiệu \(\mathbb{N}* = \mathbb{N}{\rm{\backslash }}\{ 0\} \))
Tập hợp các số nguyên \(\mathbb{Z} = \{ ...; - 3; - 2; - 1;0;1;2;3;...\} \): gồm các số nguyên âm và các số tự nhiên.
Tập hợp các số hữu tỉ \(\mathbb{Q} = \left\{ {\frac{a}{b}|a,b \in \mathbb{Z};b \ne 0} \right\}\)
(Gồm các số nguyên và các số thập phân hữu hạn hoặc vô hạn tuần hoàn)
Tập hợp các số thực\(\mathbb{R}\) gồm các số hữu tỉ và các số vô tỉ.
(Số vô tỉ là các số thập phân vô hạn không tuần hoàn).
Mối quan hệ giữa các tập hợp số: \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)
b. Các tập con thường dùng của \(\mathbb{R}\)
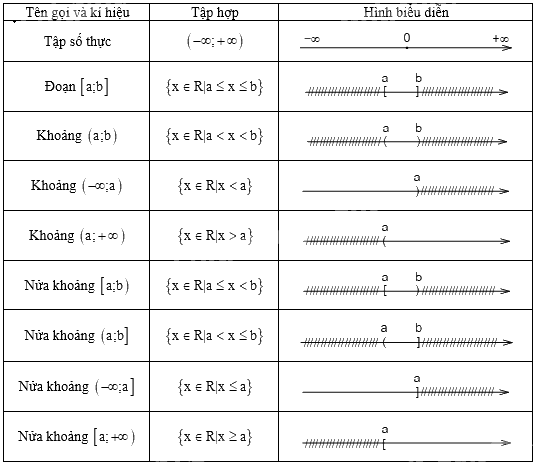
3. Các phép toán trên tập hợp
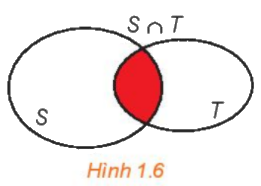
a. Giao của hai tập hợp
Giao của hai tập hợp S và T (kí hiệu \(S \cap T\)) là tập hợp gồm các phần tử thuộc cả hai tập hợp S và T.
\(S \cap T = \{ x|x \in S\) và \(x \in T\} .\)
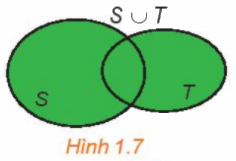
b. Hợp của hai tập hợp
Hợp của hai tập hợp S và T (kí hiệu \(S \cup T\)) là tập hợp gồm các phần tử thuộc tập hợp S hoặc thuộc T.
\(S \cup T = \{ x|x \in S\) hoặc \(x \in T\} .\)
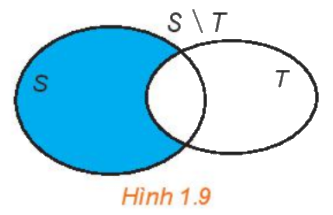
c. Hiệu của hai tập hợp
Hiệu của hai tập hợp S và T (kí hiệu \(S{\rm{\backslash }}T\)) là tập hợp gồm các phần tử thuộc S nhưng không thuộc T.
\(S{\rm{\backslash }}T = \{ x|x \in S\) và \(x \notin T\} .\)
Nếu \(T \subset S\) thì \(S{\rm{\backslash }}T\)được gọi là phần bù của T trong S, kí hiệu là \({C_S}T.\)
Ví dụ: \({C_\mathbb{Z}}\mathbb{N} = \mathbb{Z}{\rm{\backslash }}\mathbb{N} = \{ x|x \in \mathbb{Z}\) và \(x \notin \mathbb{N}\} = \{ ...; - 3; - 2; - 1\} \)
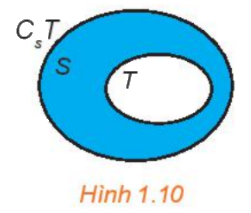
Đặc biệt: \({C_S}S = \emptyset \)
Lý thuyết tập hợp là một nhánh của toán học nghiên cứu các tập hợp, là những bộ sưu tập các đối tượng. Các đối tượng này có thể là bất kỳ thứ gì: số, người, chữ cái, hoặc thậm chí các tập hợp khác. Lý thuyết tập hợp cung cấp một ngôn ngữ và một hệ thống các quy tắc để mô tả và thao tác với các tập hợp, đóng vai trò nền tảng cho nhiều lĩnh vực toán học khác như giải tích, đại số, và xác suất.
Giả sử A = {1, 2, 3} và B = {2, 3, 4}.
Lý thuyết tập hợp có rất nhiều ứng dụng trong các lĩnh vực khác nhau:
Để củng cố kiến thức về lý thuyết tập hợp và các phép toán trên tập hợp, bạn có thể thực hành các bài tập sau:
Lý thuyết tập hợp là một công cụ mạnh mẽ và linh hoạt, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Việc nắm vững các khái niệm và phép toán cơ bản về tập hợp là rất quan trọng để hiểu và giải quyết các bài toán toán học và các vấn đề thực tế. Tại giaitoan.edu.vn, chúng tôi cam kết cung cấp cho bạn những kiến thức và kỹ năng cần thiết để thành công trong học tập và nghiên cứu toán học.