Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 68, 69, 70 sách giáo khoa Toán 10 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho hai vectơ cùng phương u=(x;y) và v=(kx;ky) Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương u=(x;y) và v=(x';y'). Tích vô hướng và góc giữa hai vectơ u=(0; - 5), v= Cho ba vectơ u = (x1;y1), v=(x2;y2), w=x3;y3 Cho tam giác ABC với A(-1; 2), B(8; -1), C(8; 8). Gọi H là trực tâm của tam giác. Một lực F không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B.
Cho hai vectơ cùng phương \(\overrightarrow u = \left( {x;y} \right)\) và \(\overrightarrow v = \left( {kx;ky} \right)\). Hãy kiểm tra công thức \(\overrightarrow u .\overrightarrow v = k\left( {{x^2} + {y^2}} \right)\) theo từng trường hợp sau:
a) \(\overrightarrow u = \overrightarrow 0 \)
b) \(\overrightarrow u \ne \overrightarrow 0 \) và \(k \ge 0\)
c) \(\overrightarrow u \ne \overrightarrow 0 \) và \(k < 0\)
Phương pháp giải:
Tính tích vô hướng bằng công thức: \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
Lời giải chi tiết:
a) Vì \(\overrightarrow u = \overrightarrow 0 \) nên \(\overrightarrow u \) vuông góc với mọi \(\overrightarrow v \).
Như vậy \(\overrightarrow u .\overrightarrow v = 0\)
Mặt khác: \(\overrightarrow u = \overrightarrow 0 \Leftrightarrow x = y = 0\)
\( \Rightarrow k\left( {{x^2} + {y^2}} \right) = 0 = \overrightarrow u .\overrightarrow v \)
b) Vì \(\overrightarrow u \ne \overrightarrow 0 \) và \(k \ge 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)cùng hướng.
\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {0^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = 1\)
\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| = \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ = \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}} = k\left( {{x^2} + {y^2}} \right)\end{array}\)
(|k|= k do k > 0)
c) Vì \(\overrightarrow u \ne \overrightarrow 0 \) và \(k < 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)ngược hướng.
\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {180^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = - 1\)
\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v = - \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| = - \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ = - \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}} = k\left( {{x^2} + {y^2}} \right).\end{array}\)
Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương \(\overrightarrow u = \left( {x;y} \right)\) và \(\overrightarrow v = \left( {x';y'} \right)\).
a) Xác định tọa độ của các điểm A và B sao cho \(\overrightarrow {OA} = \overrightarrow u ,\;\overrightarrow {OB} = \overrightarrow v .\)
b) Tính \(A{B^2},O{A^2},O{B^2}\) theo tọa độ của A và B.
c) Tính \(\overrightarrow {OA} .\overrightarrow {OB} \) theo tọa độ của A, B.
Lời giải chi tiết:
a) Vì \(\overrightarrow {OA} = \overrightarrow u = (x;y)\) nên A(x; y).
Tương tự: do \(\overrightarrow {OB} = \overrightarrow v = \left( {x';y'} \right)\) nên B (x’; y’)
b) Ta có: \(\overrightarrow {OA} = (x;y) \Rightarrow O{A^2} = {\left| {\overrightarrow {OA} } \right|^2} = {x^2} + {y^2}.\)
Và \(\overrightarrow {OB} = (x';y') \Rightarrow O{B^2} = {\left| {\overrightarrow {OB} } \right|^2} = x{'^2} + y{'^2}.\)
Lại có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {x';y'} \right) - \left( {x;y} \right) = \left( {x' - x;y' - y} \right)\)
\( \Rightarrow A{B^2} = {\left| {\overrightarrow {AB} } \right|^2} = {\left( {x' - x} \right)^2} + {\left( {y' - y} \right)^2}.\)
c) Theo định lí cosin trong tam giác OAB ta có:
\(\cos \widehat O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)
Mà \(\overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = OA.OB.\cos \widehat O\)
\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = OA.OB.\frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{2}\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{{x^2} + {y^2} + x{'^2} + y{'^2} - {{\left( {x' - x} \right)}^2} - {{\left( {y' - y} \right)}^2}}}{2}\\ \Leftrightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{ - \left( { - 2x'.x} \right) - \left( { - 2y'.y} \right)}}{2} = x'.x + y'.y\end{array}\)
Tích vô hướng và góc giữa hai vectơ \(\overrightarrow u = \left( {0; - 5} \right),\;\overrightarrow v = \left( {\sqrt 3 ;1} \right)\)
Phương pháp giải:
Cho \(\overrightarrow u = \left( {x;y} \right)\) và \(\overrightarrow v = \left( {x';y'} \right)\), khi đó: \(\overrightarrow u .\overrightarrow v = x.x' + y.y'\)
Lời giải chi tiết:
Ta có: \(\overrightarrow u = \left( {0; - 5} \right),\;\overrightarrow v = \left( {\sqrt 3 ;1} \right)\)
\( \Rightarrow \overrightarrow u .\;\,\overrightarrow v = 0.\sqrt 3 + \left( { - 5} \right).1 = - 5.\)
Cho ba vectơ \(\overrightarrow u = ({x_1};{y_1}),\;\overrightarrow v = ({x_2};{y_2}),\;\overrightarrow w = ({x_3};{y_3}).\)
a) Tính \(\overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right),\;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w \) theo tọa độ của các vectơ \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w .\)
b) So sánh \(\overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right)\) và \(\;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w \)
c) So sánh \(\;\overrightarrow u .\overrightarrow v \) và \(\overrightarrow v .\overrightarrow u \)
Phương pháp giải:
Cho \(\overrightarrow u = \left( {x;y} \right)\) và \(\overrightarrow v = \left( {x';y'} \right)\), khi đó: \(\overrightarrow u .\overrightarrow v = x.x' + y.y'\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow u = ({x_1};{y_1}),\;\overrightarrow v = ({x_2};{y_2}),\;\overrightarrow w = ({x_3};{y_3}).\)
\(\begin{array}{l} \Rightarrow \overrightarrow v + \overrightarrow w = ({x_2};{y_2}) + ({x_3};{y_3}) = \left( {{x_2} + {x_3};{y_2} + {y_3}} \right)\\ \Rightarrow \overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right) = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\end{array}\)
Và: \(\;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w = \left( {{x_1}.{x_2} + {y_1}.{y_2}} \right) + \left( {{x_1}.{x_3} + {y_1}.{y_3}} \right)\)\( = {x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}.\)
b) Vì \({x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}\)\( = \left( {{x_1}.{x_2} + {x_1}.{x_3}} \right) + \left( {{y_1}.{y_2} + {y_1}.{y_3}} \right)\)\( = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\)
Nên \(\overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right) = \;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w \)
c) Ta có: \(\overrightarrow u = ({x_1};{y_1}),\;\overrightarrow v = ({x_2};{y_2})\)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow u .\overrightarrow v = {x_1}.{x_2} + {y_1}.{y_2}\\\overrightarrow v .\overrightarrow u = {x_2}.{x_1} + {y_2}.{y_1}\end{array} \right.\)\( \Leftrightarrow \;\overrightarrow u .\overrightarrow v = \overrightarrow v .\overrightarrow u \)
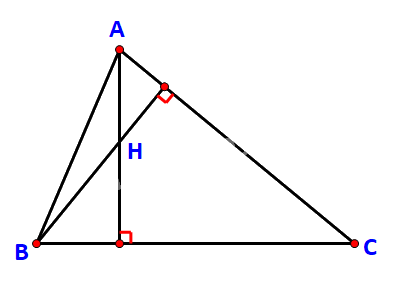
Cho tam giác ABC với A(-1; 2), B(8; -1), C(8; 8). Gọi H là trực tâm của tam giác.
a) Chứng minh rằng \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \)
b) Tìm tọa độ của H.
c) Giải tam giác ABC.
Phương pháp giải:
a) \(\overrightarrow u \bot \overrightarrow v \Leftrightarrow \overrightarrow u .\overrightarrow v = 0\)
b) Lập hệ PT biết \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \).
c) Nếu vectơ \(\overrightarrow {AB} (x;y) \) thì \(\left| {\overrightarrow {AB} } \right| = \sqrt {{x^2} + {y^2}} \)
Lời giải chi tiết:
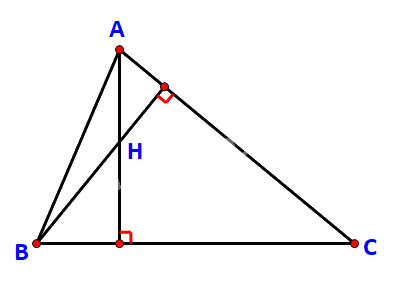
a) \( AH \bot BC\) và \(BH \bot CA\)
\( \Rightarrow \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = {90^o} \Leftrightarrow \cos \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = 0\) . Do đó \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \)
Tương tự suy ra \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \).
b) Gọi H có tọa độ (x; y)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} = (x - ( - 1);y - 2) = (x + 1;y - 2)\\\overrightarrow {BH} = (x - 8;y - ( - 1)) = (x - 8;y + 1)\end{array} \right.\)
Ta có: \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BC} = (8 - 8;8 - ( - 1)) = (0;9)\)
\((x + 1).0 + (y - 2).9 = 0 \Leftrightarrow 9.(y - 2) = 0 \Leftrightarrow y = 2.\)
Lại có: \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \) và \(\overrightarrow {CA} = ( - 1 - 8;2 - 8) = ( - 9; - 6)\)
\(\begin{array}{l}(x - 8).( - 9) + (y + 1).( - 6) = 0\\ \Leftrightarrow - 9x + 72 + 3.( - 6) = 0\\ \Leftrightarrow - 9x + 54 = 0\\ \Leftrightarrow x = 6.\end{array}\)
Vậy H có tọa độ (6; 2)
c) Ta có: \(\overrightarrow {AB} = (8 - ( - 1); - 1 - 2) = (9; - 3)\)\( \Rightarrow AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{9^2} + {{( - 3)}^2}} = 3\sqrt {10} \)
Và \(\overrightarrow {BC} = (0;9) \Rightarrow BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{0^2} + {9^2}} = 9\);
\(\overrightarrow {CA} = ( - 9; - 6)\)\( \Rightarrow AC = \left| {\overrightarrow {CA} } \right| = \sqrt {{{( - 9)}^2} + {{( - 6)}^2}} = 3\sqrt {13} .\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\cos \widehat A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{\left( {3\sqrt {13} } \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( 9 \right)}^2}}}{{2.3\sqrt {13} .3\sqrt {10} }} \approx 0,614\)\( \Rightarrow \widehat A \approx 52,{125^o}\)
\(\cos \widehat B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{{\left( 9 \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( {3\sqrt {13} } \right)}^2}}}{{2.9.3\sqrt {10} }} = \frac{{\sqrt {10} }}{{10}}\)\( \Rightarrow \widehat B \approx 71,{565^o}\)
\( \Rightarrow \widehat C \approx 56,{31^o}\)
Vậy tam giác ABC có: \(a = 9;b = 3\sqrt {13} ;c = 3\sqrt {10} \); \(\widehat A \approx 52,{125^o};\widehat B \approx 71,{565^o};\widehat C \approx 56,{31^o}.\)
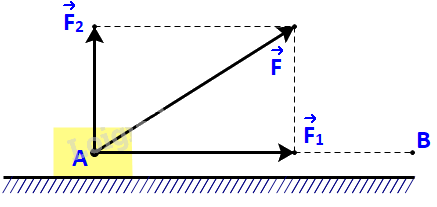
Một lực \(\overrightarrow F \) không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực \(\overrightarrow F \) được phân tích thành hai lực thành phần là \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) \((\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \;).\)
a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực \(\overrightarrow F \) (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
b) Giả sử các lực thành phần \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \)tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực \(\overrightarrow F \) và lực \(\overrightarrow {{F_1}} \).
Phương pháp giải:
Khi lực \(\overrightarrow F \) không đổi tác dụng lên một vật và điểm đặt chuyển dời một đoạn s theo hướng hợp với hướng của lực góc α thì công sinh bởi lực đó là: \(A = F.{\rm{ }}s.\cos \alpha \)
Lời giải chi tiết:
a)
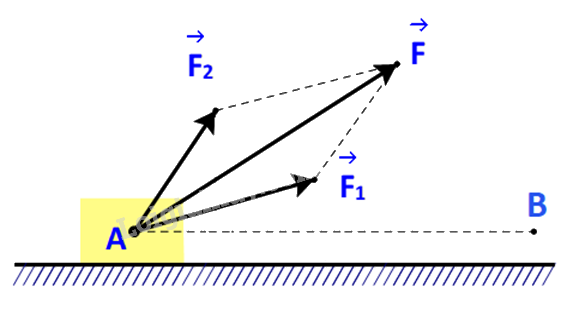
Gọi \(A,{A_1},{A_2}\) lần lượt là công sinh bởi lực \(\overrightarrow F \), \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
Ta cần chứng minh: \(A = {A_1} + {A_2}\)
Xét lực \(\overrightarrow F \), công sinh bởi lực \(\overrightarrow F \) là: \(A = \left| {\overrightarrow F } \right|.{\rm{ AB}}.\cos \left( {\overrightarrow F ,\overrightarrow {AB} } \right) = \overrightarrow F .\overrightarrow {AB} \)
Tương tự, ta có: \({A_1} = \overrightarrow {{F_1}} .\overrightarrow {AB} \), \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} \)
Áp dụng tính chất của tích vô hướng ta có:
\({A_1} + {A_2} = \overrightarrow {{F_1}} .\overrightarrow {AB} + \overrightarrow {{F_2}} .\overrightarrow {AB} = \left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right).\overrightarrow {AB} = \overrightarrow F .\overrightarrow {AB} = A\)
b)
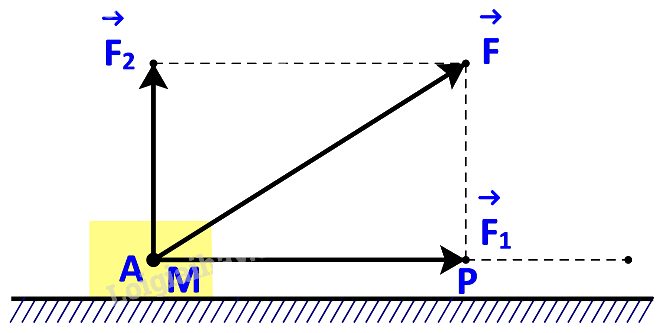
Vì \(\overrightarrow {{F_2}} \)tương ứng vuông góc với phương chuyển động nên \(\overrightarrow {{F_2}} \bot \overrightarrow {AB} \)
Do đó: công sinh bởi lực \(\overrightarrow {{F_2}} \) là: \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} = 0\)
Mà \(A = {A_1} + {A_2}\)
\( \Rightarrow A = {A_1}\)
Vậy công sinh bởi lực \(\overrightarrow F \) bằng công sinh bởi lực \(\overrightarrow {{F_1}} \).
Cho hai vectơ cùng phương \(\overrightarrow u = \left( {x;y} \right)\) và \(\overrightarrow v = \left( {kx;ky} \right)\). Hãy kiểm tra công thức \(\overrightarrow u .\overrightarrow v = k\left( {{x^2} + {y^2}} \right)\) theo từng trường hợp sau:
a) \(\overrightarrow u = \overrightarrow 0 \)
b) \(\overrightarrow u \ne \overrightarrow 0 \) và \(k \ge 0\)
c) \(\overrightarrow u \ne \overrightarrow 0 \) và \(k < 0\)
Phương pháp giải:
Tính tích vô hướng bằng công thức: \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
Lời giải chi tiết:
a) Vì \(\overrightarrow u = \overrightarrow 0 \) nên \(\overrightarrow u \) vuông góc với mọi \(\overrightarrow v \).
Như vậy \(\overrightarrow u .\overrightarrow v = 0\)
Mặt khác: \(\overrightarrow u = \overrightarrow 0 \Leftrightarrow x = y = 0\)
\( \Rightarrow k\left( {{x^2} + {y^2}} \right) = 0 = \overrightarrow u .\overrightarrow v \)
b) Vì \(\overrightarrow u \ne \overrightarrow 0 \) và \(k \ge 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)cùng hướng.
\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {0^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = 1\)
\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| = \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ = \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}} = k\left( {{x^2} + {y^2}} \right)\end{array}\)
(|k|= k do k > 0)
c) Vì \(\overrightarrow u \ne \overrightarrow 0 \) và \(k < 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)ngược hướng.
\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {180^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = - 1\)
\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v = - \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| = - \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ = - \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}} = k\left( {{x^2} + {y^2}} \right).\end{array}\)
Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương \(\overrightarrow u = \left( {x;y} \right)\) và \(\overrightarrow v = \left( {x';y'} \right)\).
a) Xác định tọa độ của các điểm A và B sao cho \(\overrightarrow {OA} = \overrightarrow u ,\;\overrightarrow {OB} = \overrightarrow v .\)
b) Tính \(A{B^2},O{A^2},O{B^2}\) theo tọa độ của A và B.
c) Tính \(\overrightarrow {OA} .\overrightarrow {OB} \) theo tọa độ của A, B.
Lời giải chi tiết:
a) Vì \(\overrightarrow {OA} = \overrightarrow u = (x;y)\) nên A(x; y).
Tương tự: do \(\overrightarrow {OB} = \overrightarrow v = \left( {x';y'} \right)\) nên B (x’; y’)
b) Ta có: \(\overrightarrow {OA} = (x;y) \Rightarrow O{A^2} = {\left| {\overrightarrow {OA} } \right|^2} = {x^2} + {y^2}.\)
Và \(\overrightarrow {OB} = (x';y') \Rightarrow O{B^2} = {\left| {\overrightarrow {OB} } \right|^2} = x{'^2} + y{'^2}.\)
Lại có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {x';y'} \right) - \left( {x;y} \right) = \left( {x' - x;y' - y} \right)\)
\( \Rightarrow A{B^2} = {\left| {\overrightarrow {AB} } \right|^2} = {\left( {x' - x} \right)^2} + {\left( {y' - y} \right)^2}.\)
c) Theo định lí cosin trong tam giác OAB ta có:
\(\cos \widehat O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)
Mà \(\overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = OA.OB.\cos \widehat O\)
\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = OA.OB.\frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{2}\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{{x^2} + {y^2} + x{'^2} + y{'^2} - {{\left( {x' - x} \right)}^2} - {{\left( {y' - y} \right)}^2}}}{2}\\ \Leftrightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{ - \left( { - 2x'.x} \right) - \left( { - 2y'.y} \right)}}{2} = x'.x + y'.y\end{array}\)
Tích vô hướng và góc giữa hai vectơ \(\overrightarrow u = \left( {0; - 5} \right),\;\overrightarrow v = \left( {\sqrt 3 ;1} \right)\)
Phương pháp giải:
Cho \(\overrightarrow u = \left( {x;y} \right)\) và \(\overrightarrow v = \left( {x';y'} \right)\), khi đó: \(\overrightarrow u .\overrightarrow v = x.x' + y.y'\)
Lời giải chi tiết:
Ta có: \(\overrightarrow u = \left( {0; - 5} \right),\;\overrightarrow v = \left( {\sqrt 3 ;1} \right)\)
\( \Rightarrow \overrightarrow u .\;\,\overrightarrow v = 0.\sqrt 3 + \left( { - 5} \right).1 = - 5.\)
Cho ba vectơ \(\overrightarrow u = ({x_1};{y_1}),\;\overrightarrow v = ({x_2};{y_2}),\;\overrightarrow w = ({x_3};{y_3}).\)
a) Tính \(\overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right),\;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w \) theo tọa độ của các vectơ \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w .\)
b) So sánh \(\overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right)\) và \(\;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w \)
c) So sánh \(\;\overrightarrow u .\overrightarrow v \) và \(\overrightarrow v .\overrightarrow u \)
Phương pháp giải:
Cho \(\overrightarrow u = \left( {x;y} \right)\) và \(\overrightarrow v = \left( {x';y'} \right)\), khi đó: \(\overrightarrow u .\overrightarrow v = x.x' + y.y'\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow u = ({x_1};{y_1}),\;\overrightarrow v = ({x_2};{y_2}),\;\overrightarrow w = ({x_3};{y_3}).\)
\(\begin{array}{l} \Rightarrow \overrightarrow v + \overrightarrow w = ({x_2};{y_2}) + ({x_3};{y_3}) = \left( {{x_2} + {x_3};{y_2} + {y_3}} \right)\\ \Rightarrow \overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right) = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\end{array}\)
Và: \(\;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w = \left( {{x_1}.{x_2} + {y_1}.{y_2}} \right) + \left( {{x_1}.{x_3} + {y_1}.{y_3}} \right)\)\( = {x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}.\)
b) Vì \({x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}\)\( = \left( {{x_1}.{x_2} + {x_1}.{x_3}} \right) + \left( {{y_1}.{y_2} + {y_1}.{y_3}} \right)\)\( = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\)
Nên \(\overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right) = \;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w \)
c) Ta có: \(\overrightarrow u = ({x_1};{y_1}),\;\overrightarrow v = ({x_2};{y_2})\)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow u .\overrightarrow v = {x_1}.{x_2} + {y_1}.{y_2}\\\overrightarrow v .\overrightarrow u = {x_2}.{x_1} + {y_2}.{y_1}\end{array} \right.\)\( \Leftrightarrow \;\overrightarrow u .\overrightarrow v = \overrightarrow v .\overrightarrow u \)
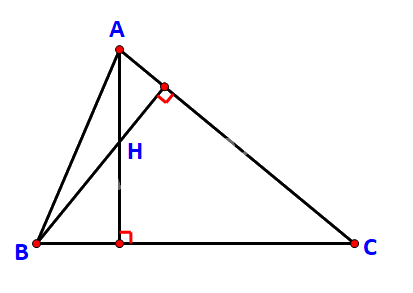
Cho tam giác ABC với A(-1; 2), B(8; -1), C(8; 8). Gọi H là trực tâm của tam giác.
a) Chứng minh rằng \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \)
b) Tìm tọa độ của H.
c) Giải tam giác ABC.
Phương pháp giải:
a) \(\overrightarrow u \bot \overrightarrow v \Leftrightarrow \overrightarrow u .\overrightarrow v = 0\)
b) Lập hệ PT biết \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \).
c) Nếu vectơ \(\overrightarrow {AB} (x;y) \) thì \(\left| {\overrightarrow {AB} } \right| = \sqrt {{x^2} + {y^2}} \)
Lời giải chi tiết:
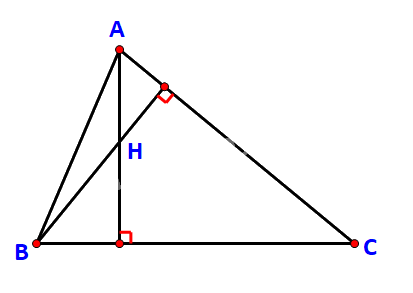
a) \( AH \bot BC\) và \(BH \bot CA\)
\( \Rightarrow \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = {90^o} \Leftrightarrow \cos \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = 0\) . Do đó \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \)
Tương tự suy ra \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \).
b) Gọi H có tọa độ (x; y)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} = (x - ( - 1);y - 2) = (x + 1;y - 2)\\\overrightarrow {BH} = (x - 8;y - ( - 1)) = (x - 8;y + 1)\end{array} \right.\)
Ta có: \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BC} = (8 - 8;8 - ( - 1)) = (0;9)\)
\((x + 1).0 + (y - 2).9 = 0 \Leftrightarrow 9.(y - 2) = 0 \Leftrightarrow y = 2.\)
Lại có: \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \) và \(\overrightarrow {CA} = ( - 1 - 8;2 - 8) = ( - 9; - 6)\)
\(\begin{array}{l}(x - 8).( - 9) + (y + 1).( - 6) = 0\\ \Leftrightarrow - 9x + 72 + 3.( - 6) = 0\\ \Leftrightarrow - 9x + 54 = 0\\ \Leftrightarrow x = 6.\end{array}\)
Vậy H có tọa độ (6; 2)
c) Ta có: \(\overrightarrow {AB} = (8 - ( - 1); - 1 - 2) = (9; - 3)\)\( \Rightarrow AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{9^2} + {{( - 3)}^2}} = 3\sqrt {10} \)
Và \(\overrightarrow {BC} = (0;9) \Rightarrow BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{0^2} + {9^2}} = 9\);
\(\overrightarrow {CA} = ( - 9; - 6)\)\( \Rightarrow AC = \left| {\overrightarrow {CA} } \right| = \sqrt {{{( - 9)}^2} + {{( - 6)}^2}} = 3\sqrt {13} .\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\cos \widehat A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{\left( {3\sqrt {13} } \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( 9 \right)}^2}}}{{2.3\sqrt {13} .3\sqrt {10} }} \approx 0,614\)\( \Rightarrow \widehat A \approx 52,{125^o}\)
\(\cos \widehat B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{{\left( 9 \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( {3\sqrt {13} } \right)}^2}}}{{2.9.3\sqrt {10} }} = \frac{{\sqrt {10} }}{{10}}\)\( \Rightarrow \widehat B \approx 71,{565^o}\)
\( \Rightarrow \widehat C \approx 56,{31^o}\)
Vậy tam giác ABC có: \(a = 9;b = 3\sqrt {13} ;c = 3\sqrt {10} \); \(\widehat A \approx 52,{125^o};\widehat B \approx 71,{565^o};\widehat C \approx 56,{31^o}.\)
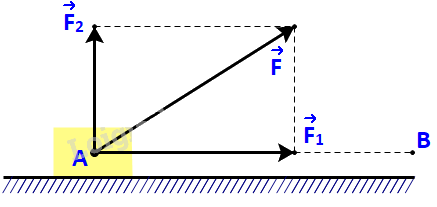
Một lực \(\overrightarrow F \) không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực \(\overrightarrow F \) được phân tích thành hai lực thành phần là \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) \((\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \;).\)
a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực \(\overrightarrow F \) (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
b) Giả sử các lực thành phần \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \)tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực \(\overrightarrow F \) và lực \(\overrightarrow {{F_1}} \).
Phương pháp giải:
Khi lực \(\overrightarrow F \) không đổi tác dụng lên một vật và điểm đặt chuyển dời một đoạn s theo hướng hợp với hướng của lực góc α thì công sinh bởi lực đó là: \(A = F.{\rm{ }}s.\cos \alpha \)
Lời giải chi tiết:
a)
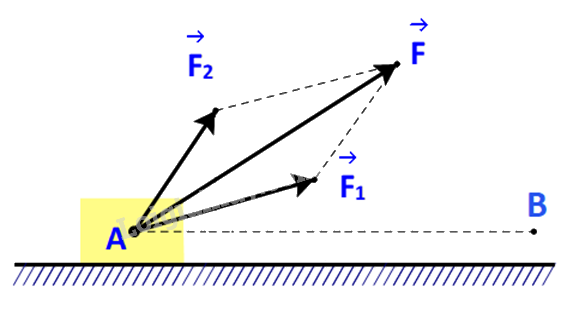
Gọi \(A,{A_1},{A_2}\) lần lượt là công sinh bởi lực \(\overrightarrow F \), \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
Ta cần chứng minh: \(A = {A_1} + {A_2}\)
Xét lực \(\overrightarrow F \), công sinh bởi lực \(\overrightarrow F \) là: \(A = \left| {\overrightarrow F } \right|.{\rm{ AB}}.\cos \left( {\overrightarrow F ,\overrightarrow {AB} } \right) = \overrightarrow F .\overrightarrow {AB} \)
Tương tự, ta có: \({A_1} = \overrightarrow {{F_1}} .\overrightarrow {AB} \), \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} \)
Áp dụng tính chất của tích vô hướng ta có:
\({A_1} + {A_2} = \overrightarrow {{F_1}} .\overrightarrow {AB} + \overrightarrow {{F_2}} .\overrightarrow {AB} = \left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right).\overrightarrow {AB} = \overrightarrow F .\overrightarrow {AB} = A\)
b)
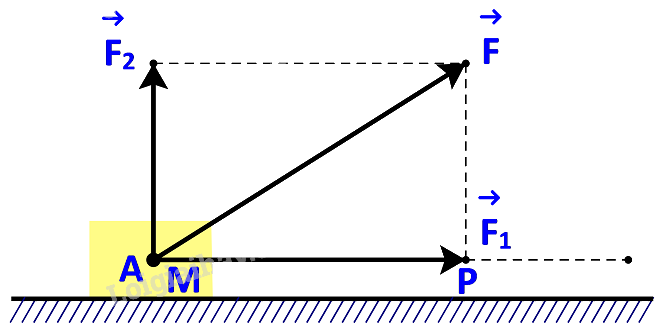
Vì \(\overrightarrow {{F_2}} \)tương ứng vuông góc với phương chuyển động nên \(\overrightarrow {{F_2}} \bot \overrightarrow {AB} \)
Do đó: công sinh bởi lực \(\overrightarrow {{F_2}} \) là: \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} = 0\)
Mà \(A = {A_1} + {A_2}\)
\( \Rightarrow A = {A_1}\)
Vậy công sinh bởi lực \(\overrightarrow F \) bằng công sinh bởi lực \(\overrightarrow {{F_1}} \).
Mục 3 trong SGK Toán 10 tập 1 - Kết nối tri thức tập trung vào việc ứng dụng các kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các công thức tính độ dài vectơ, tích vô hướng của hai vectơ, và các tính chất của vectơ để chứng minh các đẳng thức vectơ, tính góc giữa hai vectơ, và xác định vị trí tương đối của các điểm trong không gian.
Bài tập này yêu cầu học sinh tính độ dài của các vectơ cho trước. Để giải bài tập này, học sinh cần nắm vững công thức tính độ dài của vectơ: |a| = √(x² + y² + z²), trong đó a = (x, y, z).
Ví dụ: Cho vectơ a = (1, 2, 3). Tính độ dài của vectơ a.
Giải: |a| = √(1² + 2² + 3²) = √14
Bài tập này yêu cầu học sinh tính tích vô hướng của hai vectơ. Để giải bài tập này, học sinh cần nắm vững công thức tính tích vô hướng của hai vectơ: a.b = x₁x₂ + y₁y₂ + z₁z₂, trong đó a = (x₁, y₁, z₁) và b = (x₂, y₂, z₂).
Ví dụ: Cho vectơ a = (1, 2, 3) và b = (4, 5, 6). Tính tích vô hướng của hai vectơ a và b.
Giải: a.b = 1*4 + 2*5 + 3*6 = 32
Bài tập này yêu cầu học sinh chứng minh một đẳng thức vectơ. Để giải bài tập này, học sinh cần sử dụng các tính chất của vectơ, như tính chất giao hoán, tính chất kết hợp, tính chất phân phối, và các công thức liên quan đến tích vô hướng của hai vectơ.
Ví dụ: Chứng minh rằng: (a + b) . c = a.c + b.c
Giải: (a + b) . c = (x₁ + x₂)c₁ + (y₁ + y₂)c₂ + (z₁ + z₂)c₃ = x₁c₁ + x₂c₁ + y₁c₂ + y₂c₂ + z₁c₃ + z₂c₃ = (x₁c₁ + y₁c₂ + z₁c₃) + (x₂c₁ + y₂c₂ + z₂c₃) = a.c + b.c
Bài tập này yêu cầu học sinh tính góc giữa hai vectơ. Để giải bài tập này, học sinh cần sử dụng công thức tính cosin của góc giữa hai vectơ: cos(θ) = (a.b) / (|a| * |b|), trong đó θ là góc giữa hai vectơ a và b.
Ví dụ: Cho vectơ a = (1, 0, 0) và b = (0, 1, 0). Tính góc giữa hai vectơ a và b.
Giải: a.b = 0, |a| = 1, |b| = 1. cos(θ) = 0 / (1 * 1) = 0. Suy ra θ = 90°
Bài tập này yêu cầu học sinh xác định vị trí tương đối của các điểm trong không gian. Để giải bài tập này, học sinh cần sử dụng các công thức tính khoảng cách giữa hai điểm, tích vô hướng của hai vectơ, và các tính chất của vectơ.
Ví dụ: Cho ba điểm A(1, 2, 3), B(4, 5, 6), và C(7, 8, 9). Xác định xem ba điểm A, B, C có thẳng hàng hay không.
Giải: Vectơ AB = (3, 3, 3) và vectơ AC = (6, 6, 6). Ta thấy rằng vectơ AC = 2 * vectơ AB. Do đó, ba điểm A, B, C thẳng hàng.
Hy vọng rằng với lời giải chi tiết và những lời khuyên trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 3 trang 68, 69, 70 SGK Toán 10 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!