Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 60, 61, 62 sách giáo khoa Toán 10 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Chọn chuyến đi (H.8.1) Chọn vé tàu (H.8.2) Có bao nhiêu số tự nhiên từ 1 đến 30 mà không nguyên tố cùng nhau với 35?
Có bao nhiêu số tự nhiên từ 1 đến 30 mà không nguyên tố cùng nhau với 35?
Phương pháp giải:
- không nguyên tố cùng nhau = có ước chung (khác 1).
- Mà 35 =5.7 nên ta tìm các số chia hết cho 5 hoặc 7.
Lời giải chi tiết:
Từ 1 đến 30 có:
- Có 6 số chia hết cho 5 là: 5, 10, 15, 20, 25, 30.
- Có 4 số chia hết cho 7 là: 7, 14, 21, 28.
Có tất cả 6+4= 10 số tự nhiên không nguyên tố cùng nhau với 35.
Chọn chuyến đi (H.8.1)
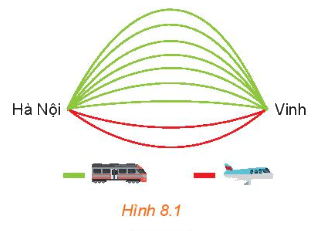
Từ Hà Nội vào Vinh mỗi ngày có 7 chuyến tàu hỏa và 2 chuyến máy bay. Bạn An muốn ngày Chủ nhật này đi từ Hà Nội vào Vinh bằng tàu hỏa hoặc máy bay.
Hỏi bạn An có bao nhiêu cách chọn?
Lời giải chi tiết:
Để đi bằng tàu hỏa bạn An có 7 cách chọn và đi bằng máy bay có 2 cách chọn.
Vậy bạn An có tất cả 7+2=9 cách chọn chuyến đi
Chọn vé tàu (H.8.2)
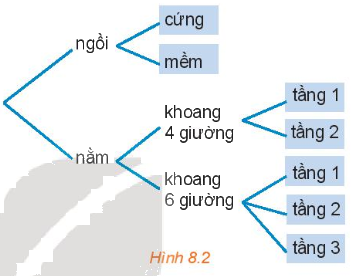
Bạn An đã quyết định mua vé tàu đi từ Hà Nội vào Vinh trên chuyến tàu SE7. Trên tàu có các toa ghế ngồi và các toa giường nằm. Toa ngồi có 2 loại vé: ngồi cứng và ngồi mềm. Toa nằm có loại không 4 giường và loại khoang 6 giường. Khoang 4 giường có hai loại vé: tầng 1 và tầng 2, khoang 6 giường có ba loại vé: tầng 1, tầng 2, tầng 3. Hỏi:
a) Có bao nhiêu loại vé ghế ngồi và bao nhiêu loại vé giường nằm?
b) Có bao nhiêu loại vé để bạn An lựa chọn?
Lời giải chi tiết:
a) Số vé ghế ngồi là 2 (loại vé)
Số vé giường nằm là 2+3=5 (loại vé)
b) Số loại vé để bạn An lựa chọn là:
2+5=7 (loại vé)
Chọn chuyến đi (H.8.1)
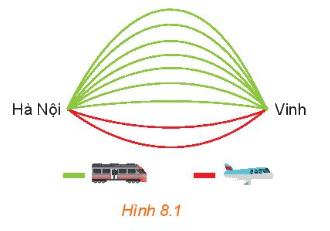
Từ Hà Nội vào Vinh mỗi ngày có 7 chuyến tàu hỏa và 2 chuyến máy bay. Bạn An muốn ngày Chủ nhật này đi từ Hà Nội vào Vinh bằng tàu hỏa hoặc máy bay.
Hỏi bạn An có bao nhiêu cách chọn?
Lời giải chi tiết:
Để đi bằng tàu hỏa bạn An có 7 cách chọn và đi bằng máy bay có 2 cách chọn.
Vậy bạn An có tất cả 7+2=9 cách chọn chuyến đi
Chọn vé tàu (H.8.2)
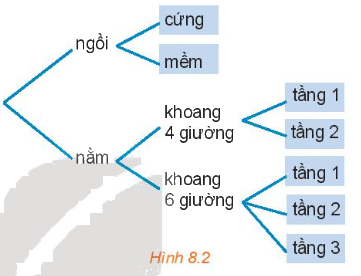
Bạn An đã quyết định mua vé tàu đi từ Hà Nội vào Vinh trên chuyến tàu SE7. Trên tàu có các toa ghế ngồi và các toa giường nằm. Toa ngồi có 2 loại vé: ngồi cứng và ngồi mềm. Toa nằm có loại không 4 giường và loại khoang 6 giường. Khoang 4 giường có hai loại vé: tầng 1 và tầng 2, khoang 6 giường có ba loại vé: tầng 1, tầng 2, tầng 3. Hỏi:
a) Có bao nhiêu loại vé ghế ngồi và bao nhiêu loại vé giường nằm?
b) Có bao nhiêu loại vé để bạn An lựa chọn?
Lời giải chi tiết:
a) Số vé ghế ngồi là 2 (loại vé)
Số vé giường nằm là 2+3=5 (loại vé)
b) Số loại vé để bạn An lựa chọn là:
2+5=7 (loại vé)
Có bao nhiêu số tự nhiên từ 1 đến 30 mà không nguyên tố cùng nhau với 35?
Phương pháp giải:
- không nguyên tố cùng nhau = có ước chung (khác 1).
- Mà 35 =5.7 nên ta tìm các số chia hết cho 5 hoặc 7.
Lời giải chi tiết:
Từ 1 đến 30 có:
- Có 6 số chia hết cho 5 là: 5, 10, 15, 20, 25, 30.
- Có 4 số chia hết cho 7 là: 7, 14, 21, 28.
Có tất cả 6+4= 10 số tự nhiên không nguyên tố cùng nhau với 35.
Mục 1 của chương trình Toán 10 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về vectơ. Các bài tập trong trang 60, 61, 62 SGK Toán 10 tập 2 yêu cầu học sinh vận dụng các khái niệm và tính chất của vectơ để giải quyết các bài toán thực tế. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán là vô cùng quan trọng để hoàn thành tốt các bài tập này.
Bài 1 thường bao gồm các câu hỏi trắc nghiệm và bài tập tự luận về định nghĩa, các phép toán trên vectơ (cộng, trừ, nhân với một số), và các tính chất của vectơ. Để giải tốt bài 1, học sinh cần nắm vững các khái niệm cơ bản và hiểu rõ các quy tắc thực hiện các phép toán trên vectơ.
Bài 2 thường liên quan đến việc sử dụng vectơ để chứng minh các tính chất hình học, chẳng hạn như chứng minh hai đường thẳng song song, chứng minh hai tam giác bằng nhau, hoặc tính diện tích hình bình hành. Để giải tốt bài 2, học sinh cần kết hợp kiến thức về vectơ với kiến thức về hình học.
Bài 3 thường liên quan đến việc sử dụng vectơ để mô tả các đại lượng vật lý như vận tốc, gia tốc, lực. Để giải tốt bài 3, học sinh cần hiểu rõ ý nghĩa vật lý của vectơ và biết cách áp dụng các phép toán trên vectơ để giải quyết các bài toán vật lý.
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 1 trang 60, 61, 62 SGK Toán 10 tập 2 - Kết nối tri thức:
Để hiểu sâu hơn về vectơ và các ứng dụng của nó, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với hướng dẫn chi tiết và các mẹo giải nhanh trên, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 1 trang 60, 61, 62 SGK Toán 10 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!