Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 4.5 trang 50 SGK Toán 10 tập 1 – Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin chinh phục môn Toán.
Trên mặt phẳng tọa độ Oxy hãy vẽ các vecto OA, MN với A (1; 2), M (0; -1), N (3; 5).
Đề bài
Trên mặt phẳng tọa độ Oxy hãy vẽ các vecto \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) với A (1; 2), M (0; -1), N (3; 5).
a) Chỉ ra mỗi quan hệ giữa hai vecto trên.
b) Một vật thể khởi hành từ M chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn vởi vecto \(\overrightarrow v = \overrightarrow {OA} \). Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu sẽ tới N?
Lời giải chi tiết
a)
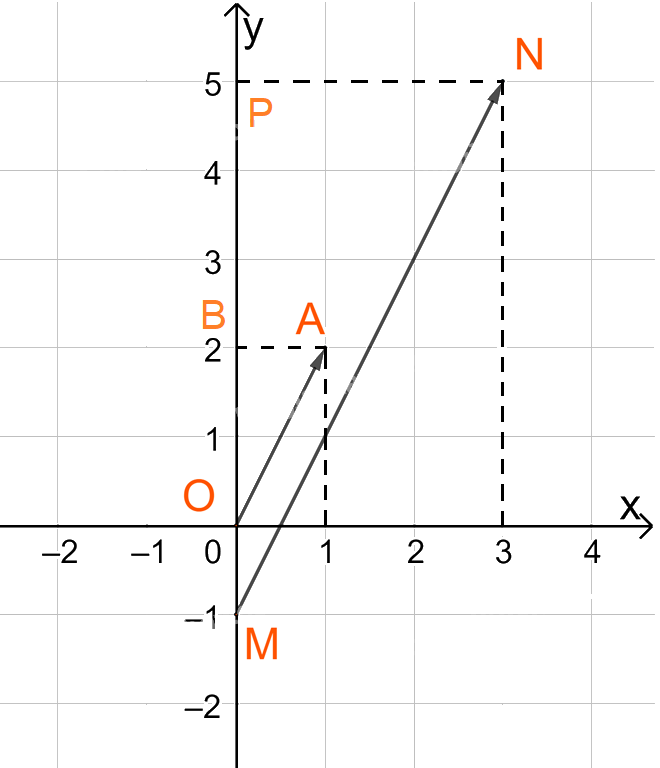
Lấy điểm B(0;2) và P(0;5).
Ta có: OB=2, AB =1, MP=6 và PN=3.
Xét hai tam giác vuông OBA và MPN ta có: \(\frac{{OB}}{{MP}} = \frac{{AB}}{{PN}} = \frac{1}{3}\)
Do đó hai tam giác đồng dạng và OA // MN.
Suy ra \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) cùng phương.
Hơn nữa, \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) cùng hướng và MN = 3 OA.
b) Mỗi giờ, vật thể đó đi được quãng đường tương ứng với đoạn thẳng OA.
Vì \({MN} = 3. {OA} \) nên vật thể đó sẽ đi qua N sau 3 giờ kể từ lúc khởi hành.
Bài 4.5 trang 50 SGK Toán 10 tập 1 – Kết nối tri thức thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và đặc biệt là ứng dụng của vectơ trong việc chứng minh các tính chất hình học.
Bài 4.5 thường bao gồm các dạng bài tập sau:
Để giải bài 4.5 trang 50 SGK Toán 10 tập 1 – Kết nối tri thức, chúng ta cần thực hiện các bước sau:
Ví dụ minh họa:
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh AB. Chứng minh rằng vectơ CM = 1/2 * (vectơ AD + vectơ AB).
Lời giải:
Ta có: vectơ CM = vectơ CA + vectơ AM
Mà vectơ CA = vectơ CB + vectơ BA = vectơ AD + vectơ BA
Và vectơ AM = 1/2 * vectơ AB
Do đó, vectơ CM = vectơ AD + vectơ BA + 1/2 * vectơ AB = vectơ AD + 3/2 * vectơ AB
Tuy nhiên, cách giải trên chưa chính xác. Cách giải đúng như sau:
Ta có: vectơ CM = vectơ CA + vectơ AM
Mà vectơ CA = vectơ CD + vectơ DA = vectơ BA + vectơ DA
Và vectơ AM = 1/2 * vectơ AB
Do đó, vectơ CM = vectơ BA + vectơ DA + 1/2 * vectơ AB = 3/2 * vectơ AB + vectơ DA = 1/2 * (vectơ AD + vectơ AB)
Để củng cố kiến thức về vectơ, bạn có thể tham khảo các bài tập tương tự sau:
Bài 4.5 trang 50 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về vectơ và ứng dụng của vectơ trong hình học. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, bạn sẽ tự tin giải quyết bài tập này một cách hiệu quả.