Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 2 - Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức Toán học một cách nhanh chóng và hiệu quả nhất. Hãy cùng khám phá lời giải cho mục 1 trang 5, 6 SGK Toán 10 tập 2 ngay bây giờ!
Bảng 6.1 cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong ngày 25-3-2021 tại một trạm quan trắc ở thủ đô Hà Nội: a) Thời gian theo dõi mực nước biển ở Trường Sa được thể hiện trong hình từ năm nào đến năm nào? a) Dựa vào bảng 6.2 về già bán lẻ điện sinh hoạt, hãy tính số tiền phải trả ứng với mỗi lượng điện tiêu thụ ở Bảng 6.3: a) Hãy cho biết Bảng 6.4 có cho ta một hàm số hay không. Nếu có, tìm tập xác định và tập giá trị của hàm số đó.
Quan sát hóa đơn tiền điện ở hình bên. Hãy cho biết tổng lượng điện tiêu thụ trong tháng và số tiền phải trả (chưa tính thuế giá trị gia tăng). Có cách nào mô tả sự phụ thuộc của số tiền phải trả vào tổng lượng điện tiêu thụ hay không?
Bảng 6.1 cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong ngày 25-3-2021 tại một trạm quan trắc ở thủ đô Hà Nội:

a) Hãy cho biết nồng độ bụi PM 2.5 tại mỗi thời điểm 8 giờ, 12 giờ, 16 giờ.
b) Trong Bảng 6.1, mỗi thời điểm tương ứng với bao nhiêu giá trị của nồng độ bụi PM 2.5?
Lời giải chi tiết:
a) Dựa vào Bảng 6.1, ta thấy:
- Tại thời điểm 8 giờ, nồng độ bụi PM 2.5 là 57,9 \(\)
- Tại thời điểm 12 giờ, nồng độ bụi PM 2.5 là 69,07
- Tại thời điểm 16 giờ, nồng độ bụi PM 2.5 là 81,78
b) Trong Bảng 6.1, mỗi thời điểm tương ứng với 1 giá trị của nồng độ bụi PM 2.5
Ví dụ: tại 0 giờ, nồng độ bụi PM 2.5 là 74,27
a) Hãy cho biết Bảng 6.4 có cho ta một hàm số hay không. Nếu có, tìm tập xác định và tập giá trị của hàm số đó.

b) Trở lại HĐ2, ta có hàm số cho bằng biểu đồ. Hãy cho biết giá trị của hàm số tại x=2018. Tìm tập xác định, tập giá trị của hàm số đó.
c) Cho hàm số \(y = f(x) = - 2{x^2}\). Tính f(1); f(2) và tìm tập xác định, tập giá trị của hàm số này.
Phương pháp giải:
Tập xác định là tập D với mỗi giá trị của x sẽ thuộc tập D
Tập tất cả giá trị y nhận được là tập giá trị của hàm số
Lời giải chi tiết:
a) Mỗi giá trị của x tương ứng sẽ có 1 giá trị của y nên Bảng 6.4 cho ta một hàm số.
Tập xác định của hàm số \(D = \left\{ {2013;2014;2015;2016;2017;2018} \right\}\)
Tập giá trị của hàm số \(\left\{ {73,1;73,2;73,3;73,4;73,5} \right\}\)
b) Giá trị của hàm số tại x=2018 là 242
Tập xác định của hàm số \(D = \left( {2013;2019} \right)\)
Tập giá trị của hàm số \(\left( {236;242} \right)\)
c)\(\)\(\begin{array}{l}f(1) = - {2.1^2} = - 2\\f(2) = - {2.2^2} = - 8\end{array}\)
Tập xác định của hàm số \(y = f(x) = - 2{x^2}\)là \(\mathbb{R}\)
Ta có \({x^2} \ge 0 \Rightarrow - 2{x^2} \le 0\) , do đó \(y \le 0\)
Tập giá trị của hàm số \(y = f(x) = - 2{x^2}\) là \(\left( { - \infty ;0} \right)\)
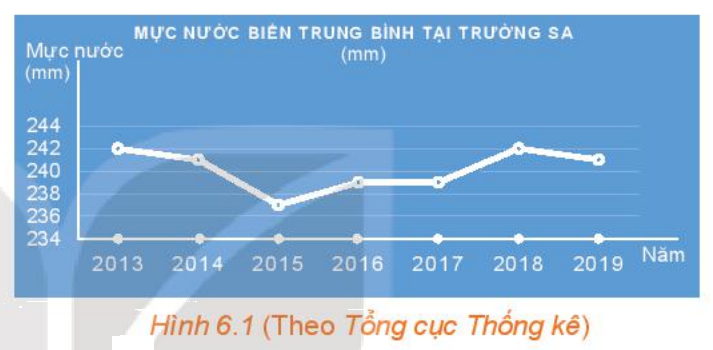
Quan sát Hình 6.1.
a) Thời gian theo dõi mực nước biển ở Trường Sa được thể hiện trong hình từ năm nào đến năm nào?
b) Trong khoảng thời gian đó, năm nào mực nước biển trung bình tại Trường Sa cao nhất, thấp nhất?
Lời giải chi tiết:
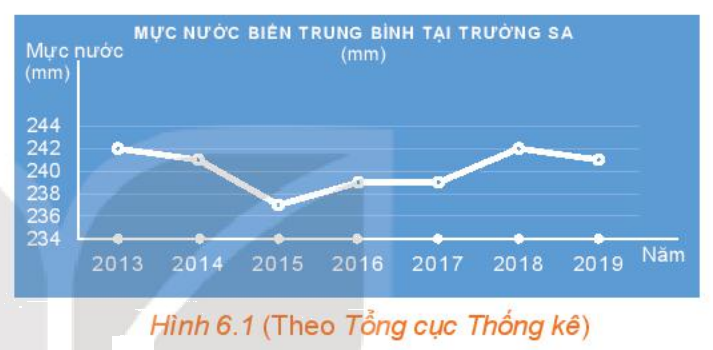
a) Quan sát biểu đồ trên, ta biết được thời gian theo dõi mực nước biển ở Trường Sa được thể hiện từ năm 2013 đến năm 2019
b) Trong khoảng thời gian đó:
- Năm 2013, 2018 là năm có mực nước cao nhất
- Năm 2015 là năm có mực nước thấp nhất
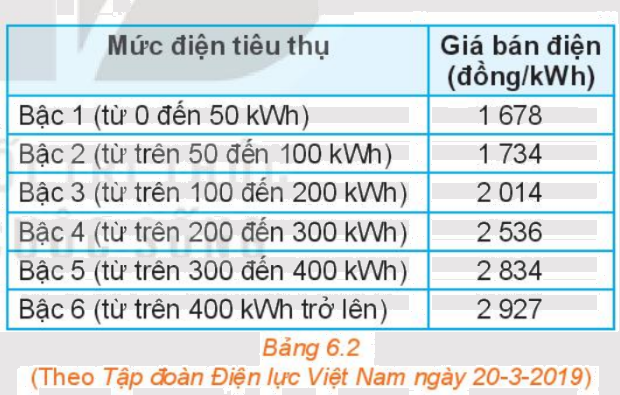
a) Dựa vào bảng 6.2 về già bán lẻ điện sinh hoạt, hãy tính số tiền phải trả ứng với mỗi lượng điện tiêu thụ ở Bảng 6.3:
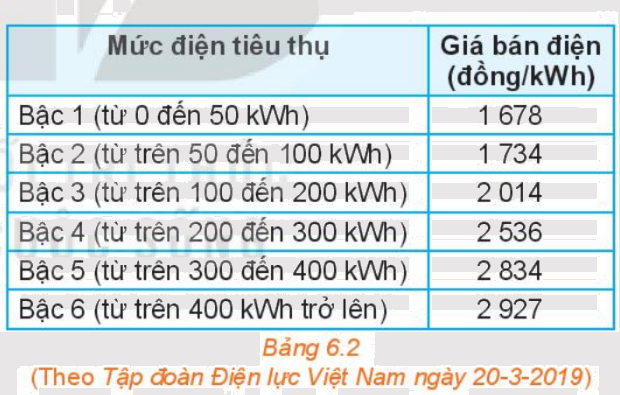
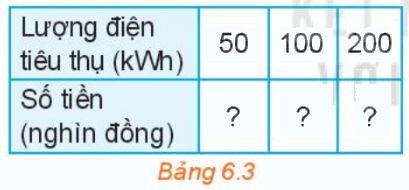
b) Gọi x là lượng điện tiêu thụ (đơn vị kWh) và y là số tiền phải trả tương ứng (đơn vị nghìn đồng). Hãy viết công thức mô tả sự phụ thuộc của y vào x khi \(0 \le x \le 50\)
Phương pháp giải:
Dựa vào Bảng 6.2, ta xem xét lượng điện tiêu thụ nằm ở bậc nào, từ đó ta tính được số tiền và công thức mô tả.
Lời giải chi tiết:
a) Số tiền phải trả tương ứng với lượng điện 50kWh là:
\(50.1,678 = 83,9\) (nghìn đồng)
Số tiền phải trả tương ứng với lượng điện 100kWh là:
\(50.1,678 + (100 - 50).1,734 = 170,6\)(nghìn đồng)
Số tiền phải trả tương ứng với lượng điện 200kWh là:
\(50.1,678 + (100 - 50).1,734 + (200 - 100).2,014 = 372\)(nghìn đồng)
Điền vào bảng ta có:
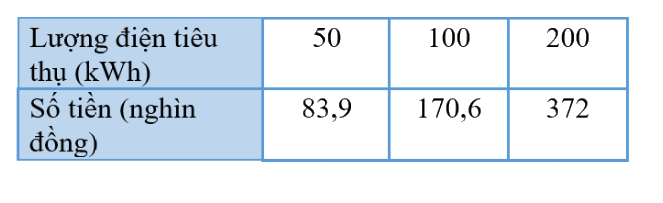
b) Công thức mô tả sự phụ thuộc y vào x khi\(0 \le x \le 50\) là:
\(y = 1,678.x\)
Quan sát hóa đơn tiền điện ở hình bên. Hãy cho biết tổng lượng điện tiêu thụ trong tháng và số tiền phải trả (chưa tính thuế giá trị gia tăng). Có cách nào mô tả sự phụ thuộc của số tiền phải trả vào tổng lượng điện tiêu thụ hay không?
Bảng 6.1 cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong ngày 25-3-2021 tại một trạm quan trắc ở thủ đô Hà Nội:

a) Hãy cho biết nồng độ bụi PM 2.5 tại mỗi thời điểm 8 giờ, 12 giờ, 16 giờ.
b) Trong Bảng 6.1, mỗi thời điểm tương ứng với bao nhiêu giá trị của nồng độ bụi PM 2.5?
Lời giải chi tiết:
a) Dựa vào Bảng 6.1, ta thấy:
- Tại thời điểm 8 giờ, nồng độ bụi PM 2.5 là 57,9 \(\)
- Tại thời điểm 12 giờ, nồng độ bụi PM 2.5 là 69,07
- Tại thời điểm 16 giờ, nồng độ bụi PM 2.5 là 81,78
b) Trong Bảng 6.1, mỗi thời điểm tương ứng với 1 giá trị của nồng độ bụi PM 2.5
Ví dụ: tại 0 giờ, nồng độ bụi PM 2.5 là 74,27
Quan sát Hình 6.1.
a) Thời gian theo dõi mực nước biển ở Trường Sa được thể hiện trong hình từ năm nào đến năm nào?
b) Trong khoảng thời gian đó, năm nào mực nước biển trung bình tại Trường Sa cao nhất, thấp nhất?
Lời giải chi tiết:
a) Quan sát biểu đồ trên, ta biết được thời gian theo dõi mực nước biển ở Trường Sa được thể hiện từ năm 2013 đến năm 2019
b) Trong khoảng thời gian đó:
- Năm 2013, 2018 là năm có mực nước cao nhất
- Năm 2015 là năm có mực nước thấp nhất
a) Dựa vào bảng 6.2 về già bán lẻ điện sinh hoạt, hãy tính số tiền phải trả ứng với mỗi lượng điện tiêu thụ ở Bảng 6.3:
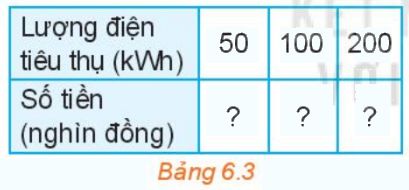
b) Gọi x là lượng điện tiêu thụ (đơn vị kWh) và y là số tiền phải trả tương ứng (đơn vị nghìn đồng). Hãy viết công thức mô tả sự phụ thuộc của y vào x khi \(0 \le x \le 50\)
Phương pháp giải:
Dựa vào Bảng 6.2, ta xem xét lượng điện tiêu thụ nằm ở bậc nào, từ đó ta tính được số tiền và công thức mô tả.
Lời giải chi tiết:
a) Số tiền phải trả tương ứng với lượng điện 50kWh là:
\(50.1,678 = 83,9\) (nghìn đồng)
Số tiền phải trả tương ứng với lượng điện 100kWh là:
\(50.1,678 + (100 - 50).1,734 = 170,6\)(nghìn đồng)
Số tiền phải trả tương ứng với lượng điện 200kWh là:
\(50.1,678 + (100 - 50).1,734 + (200 - 100).2,014 = 372\)(nghìn đồng)
Điền vào bảng ta có:
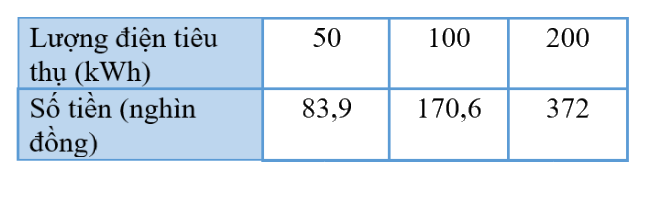
b) Công thức mô tả sự phụ thuộc y vào x khi\(0 \le x \le 50\) là:
\(y = 1,678.x\)
a) Hãy cho biết Bảng 6.4 có cho ta một hàm số hay không. Nếu có, tìm tập xác định và tập giá trị của hàm số đó.

b) Trở lại HĐ2, ta có hàm số cho bằng biểu đồ. Hãy cho biết giá trị của hàm số tại x=2018. Tìm tập xác định, tập giá trị của hàm số đó.
c) Cho hàm số \(y = f(x) = - 2{x^2}\). Tính f(1); f(2) và tìm tập xác định, tập giá trị của hàm số này.
Phương pháp giải:
Tập xác định là tập D với mỗi giá trị của x sẽ thuộc tập D
Tập tất cả giá trị y nhận được là tập giá trị của hàm số
Lời giải chi tiết:
a) Mỗi giá trị của x tương ứng sẽ có 1 giá trị của y nên Bảng 6.4 cho ta một hàm số.
Tập xác định của hàm số \(D = \left\{ {2013;2014;2015;2016;2017;2018} \right\}\)
Tập giá trị của hàm số \(\left\{ {73,1;73,2;73,3;73,4;73,5} \right\}\)
b) Giá trị của hàm số tại x=2018 là 242
Tập xác định của hàm số \(D = \left( {2013;2019} \right)\)
Tập giá trị của hàm số \(\left( {236;242} \right)\)
c)\(\)\(\begin{array}{l}f(1) = - {2.1^2} = - 2\\f(2) = - {2.2^2} = - 8\end{array}\)
Tập xác định của hàm số \(y = f(x) = - 2{x^2}\)là \(\mathbb{R}\)
Ta có \({x^2} \ge 0 \Rightarrow - 2{x^2} \le 0\) , do đó \(y \le 0\)
Tập giá trị của hàm số \(y = f(x) = - 2{x^2}\) là \(\left( { - \infty ;0} \right)\)
Mục 1 của SGK Toán 10 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Hàm số bậc hai. Đây là một phần quan trọng, nền tảng cho các kiến thức toán học nâng cao hơn. Việc nắm vững các khái niệm, tính chất và phương pháp giải bài tập trong mục này là vô cùng cần thiết.
Bài tập này yêu cầu học sinh xác định tập xác định của các hàm số được cho. Để giải bài tập này, cần nắm vững khái niệm về tập xác định của hàm số và các điều kiện để hàm số có nghĩa.
Ví dụ: Hàm số y = √(x - 2) có tập xác định là x ≥ 2.
Bài tập này yêu cầu học sinh xét tính chẵn, lẻ của các hàm số được cho. Để giải bài tập này, cần nắm vững định nghĩa về hàm số chẵn, hàm số lẻ và các phương pháp kiểm tra tính chẵn, lẻ của hàm số.
Ví dụ: Hàm số y = x2 là hàm số chẵn vì y(-x) = y(x).
Bài tập này yêu cầu học sinh tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước. Để giải bài tập này, cần nắm vững các phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, chẳng hạn như phương pháp sử dụng đạo hàm hoặc phương pháp sử dụng tính chất của hàm số.
Bài tập này yêu cầu học sinh giải các phương trình bậc hai. Để giải bài tập này, cần nắm vững công thức nghiệm của phương trình bậc hai và các phương pháp giải phương trình bậc hai, chẳng hạn như phương pháp phân tích thành nhân tử hoặc phương pháp sử dụng công thức nghiệm.
Bài tập này yêu cầu học sinh giải các bất phương trình bậc hai. Để giải bài tập này, cần nắm vững phương pháp giải bất phương trình bậc hai và các điều kiện để bất phương trình có nghiệm.
Toán 10 là một môn học quan trọng, nền tảng cho các môn học khác. Để học tốt Toán 10, cần:
Chúc bạn học tốt Toán 10!