Bất phương trình bậc nhất hai ẩn là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán học lớp 10. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, chi tiết và dễ hiểu về lý thuyết bất phương trình bậc nhất hai ẩn, giúp bạn tự tin chinh phục môn Toán.
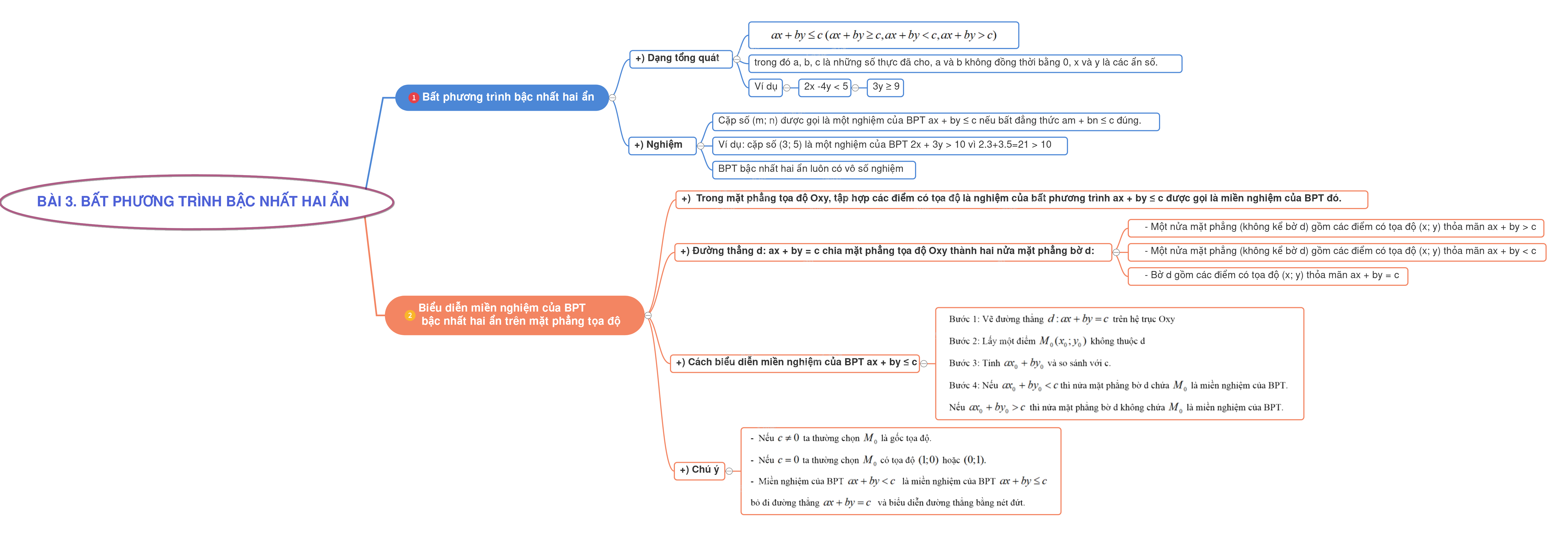
1. Bất phương trình bậc nhất hai ẩn 2. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ
1. Bất phương trình bậc nhất hai ẩn
+) Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là:
\(ax + by \le c\;(ax + by \ge c,ax + by < c,ax + by > c)\) trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.
Ví dụ: \(2x + 3y > 10\)
+) Cặp số \(({x_0};{y_0})\) được gọi là một nghiệm của BPT bậc nhất hai ẩn \(ax + by \le c\;\)nếu bất đẳng thức \(a{x_0} + b{y_0} \le c\;\)đúng.
Ví dụ: cặp số \((3;5)\) là một nghiệm của BPT \(2x + 3y > 10\) vì \(2.3 + 3.5 = 21 > 10\)
+) BPT bậc nhất hai ẩn luôn có vô số nghiệm.
2. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ
+) Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương trình \(ax + by \le c\;\)được gọi là miền nghiệm của BPT đó.
+) Đường thẳng \(d:ax + by = c\;\)chia mặt phẳng tọa độ Oxy thành hai nửa mặt phẳng bờ d:
- Một nửa mặt phẳng (không kể bờ d) gồm các điểm có tọa độ (x; y) thỏa mãn \(ax + by > c\)
- Một nửa mặt phẳng (không kể bờ d) gồm các điểm có tọa độ (x; y) thỏa mãn \(ax + by < c\)
- Bờ d gồm các điểm có tọa độ (x; y) thỏa mãn \(ax + by = c\)
+) Cách biểu diễn miền nghiệm của BPT \(ax + by \le c\;\)
Bước 1: Vẽ đường thẳng \(d:ax + by = c\;\)trên hệ trục Oxy
Bước 2: Lấy một điểm \({M_0}({x_0};{y_0})\) không thuộc d
Bước 3: Tính \(a{x_0} + b{y_0}\) và so sánh với c.
Bước 4: Nếu \(a{x_0} + b{y_0} < c\)thì nửa mặt phẳng bờ d chứa \({M_0}\) là miền nghiệm của bất phương trình. Nếu \(a{x_0} + b{y_0} > c\) thì nửa mặt phẳng bờ d không chứa \({M_0}\) là miền nghiệm của BPT.
* Chú ý:
- Nếu \(c \ne 0\) ta thường chọn \({M_0}\) là gốc tọa độ.
- Nếu \(c = 0\) ta thường chọn \({M_0}\) có tọa độ \((1;0)\) hoặc \((0;1).\)
- Miền nghiệm của BPT \(ax + by < c\;\) là miền nghiệm của BPT \(ax + by \le c\;\)bỏ đi đường thẳng \(ax + by = c\;\) và biểu diễn đường thẳng bằng nét đứt.
Bất phương trình bậc nhất hai ẩn là một công cụ toán học mạnh mẽ, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Hiểu rõ lý thuyết và cách giải các loại bất phương trình này là nền tảng quan trọng cho việc học tập và nghiên cứu toán học ở các cấp độ cao hơn.
Bất phương trình bậc nhất hai ẩn là bất phương trình có dạng:
ax + by < c (hoặc ax + by ≤ c, ax + by > c, ax + by ≥ c)Trong đó:
Tập nghiệm của bất phương trình bậc nhất hai ẩn là tập hợp tất cả các cặp số (x; y) thỏa mãn bất phương trình đã cho.
Để biểu diễn tập nghiệm trên mặt phẳng tọa độ, ta vẽ đường thẳng ax + by = c. Đường thẳng này chia mặt phẳng thành hai nửa mặt phẳng. Tập nghiệm của bất phương trình là một nửa mặt phẳng (bao gồm cả đường thẳng nếu bất phương trình có dấu bằng).
Để xác định miền nghiệm của bất phương trình ax + by < c, ta thực hiện các bước sau:
Hệ bất phương trình bậc nhất hai ẩn là tập hợp các bất phương trình bậc nhất hai ẩn được viết cùng nhau. Tập nghiệm của hệ bất phương trình là tập hợp tất cả các cặp số (x; y) thỏa mãn tất cả các bất phương trình trong hệ.
Để tìm tập nghiệm của hệ bất phương trình, ta tìm giao của các miền nghiệm của từng bất phương trình trong hệ.
Ví dụ 1: Giải bất phương trình 2x + y ≤ 4
Bước 1: Vẽ đường thẳng 2x + y = 4.
Bước 2: Chọn điểm O(0; 0). Thay vào bất phương trình, ta có 2(0) + 0 ≤ 4, bất phương trình đúng.
Bước 3: Miền nghiệm là nửa mặt phẳng chứa gốc tọa độ O(0; 0), bao gồm cả đường thẳng 2x + y = 4.
Ví dụ 2: Giải hệ bất phương trình:
Giải từng bất phương trình, ta tìm được hai miền nghiệm. Giao của hai miền nghiệm này là tập nghiệm của hệ bất phương trình.
Bất phương trình bậc nhất hai ẩn có nhiều ứng dụng trong thực tế, ví dụ:
Để nắm vững lý thuyết và kỹ năng giải bất phương trình bậc nhất hai ẩn, bạn nên luyện tập thường xuyên với các bài tập khác nhau. giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn củng cố kiến thức và tự tin hơn trong các kỳ thi.
Hy vọng với những kiến thức và ví dụ minh họa trên, bạn đã có cái nhìn tổng quan và hiểu rõ hơn về lý thuyết bất phương trình bậc nhất hai ẩn. Chúc bạn học tập tốt!