Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 3, trang 16, 17 và 18 của sách giáo khoa Toán 10 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Viết tập hợp X gồm những thành viên tham gia cả hai chuyên đề 1 và 2 trong tình huống mở đầu. Cho các tập hợp C = [1; 5], D = [-2; 3]. Hãy xác định tập hợp Trở lại tình huống mở đầu, hãy xác định tập hợp các thành viên tham gia Chuyên đề 1 hoặc Chuyên đề 2. Trở lại tình huống mở đầu, hãy xác định tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2. Tìm phần bù của các tập hợp sau trong R
Trở lại tình huống mở đầu, hãy xác định tập hợp các thành viên tham gia Chuyên đề 1 hoặc Chuyên đề 2.
Lời giải chi tiết:
Kí hiệu H là tập hợp tất cả các thành viên tham gia chuyên đề 1 hoặc chuyên đề 2.
Tập hợp các bạn tham gia chuyên đề 1: A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
Tập hợp các bạn tham gia chuyên đề 2: B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Vậy H = {Nam; Ngân; Hân; Hiền; Lam; Khánh; Bình; Hương; Chi; Tú }
Chú ý khi giải
Mỗi phần tử chỉ liệt kê một lần.
Trở lại tình huống mở đầu, hãy xác định tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2.
Lời giải chi tiết:
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
X = {Khánh; Bình; Hương; Chi; Tú }
Có Nam và Ngân chỉ tham gia chuyên đề 1.
Tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2 là
G = {Nam; Ngân}
Cho các tập hợp C = [1; 5], D = [-2; 3]. Hãy xác định tập hợp \(C \cap \;D\).
Lời giải chi tiết:
Ta có:

Giao của hai tập hợp C và D là \(C \cap \;D = \left[ {1;3} \right]\).
Hãy biểu diễn tập hợp \(A \cup \;\,B\) bằng biểu đồ Ven, với A, B được cho trong HĐ1
Lời giải chi tiết:
Ta có:
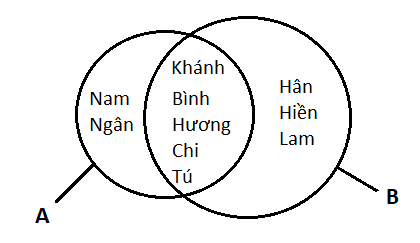
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Biểu đồ Ven
Lớp 10A có 24 bạn tham gia thi đấu bóng đá và cầu lông, trong đó có 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông. Giả sử các trận bóng đá và cầu lông không tổ chức đồng thời. Hỏi có bao nhiêu bạn lớp 10A tham gia thi đấu cả bóng đá và cầu lông?
Phương pháp giải:
Gọi x là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Sử dụng biểu đồ Ven để mô tả các tập hợp.
Lời giải chi tiết:
Gọi \(x\) là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Ta có: 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông
\( \Rightarrow \) Có \(16 - x\) bạn chỉ tham gia thi đấu bóng đá mà không thi đấu cầu lông.
Và có \(11 - x\) bạn chỉ tham gia thi đấu cầu lông mà không thi đấu bóng đá.
Ta có biểu đồ Ven như sau:
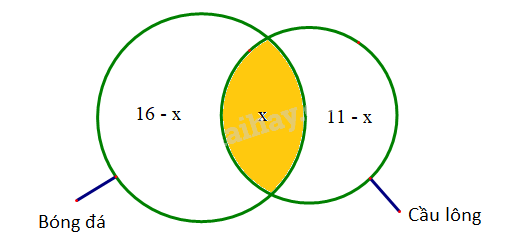
Tổng số bạn tham gia thi đấu bóng đá và cầu lông là: 16-x + x + 11-x = 24 => x=3.
Vậy lớp 10A có 3 bạn tham ggia thi đấu cả bóng đá và cầu lông.
Tìm phần bù của các tập hợp sau trong \(\mathbb{R}\):
a) \(\left( { - \infty ; - 2} \right)\)
b) \([ - 5; + \infty )\)
Phương pháp giải:
Biểu diễn các tập hợp trên trục số.
Lời giải chi tiết:
Ta có:

Suy ra phần bù của tập hợp \(\left( { - \infty ; - 2} \right)\) trong \(\mathbb{R}\) là: \(\mathbb{R}{\rm{\backslash }}\left( { - \infty ; - 2} \right) = [ - 2; + \infty )\)

Suy ra phần bù của tập hợp \([ - 5; + \infty )\) trong \(\mathbb{R}\) là: \(\mathbb{R}{\rm{\backslash }}[ - 5; + \infty ) = ( - \infty ; - 5)\)
Viết tập hợp X gồm những thành viên tham gia cả hai chuyên đề 1 và 2 trong tình huống mở đầu.
Tập X có phải là tập con của tập A không? Tập X có phải là tập con của tập B không? (A, B là các tập hợp trong HĐ1).
Lời giải chi tiết:

X = {Khánh; Bình; Hương; Chi; Tú}
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Dễ thấy: Các phần tử của X đều là phần tử của tập hợp A và tập hợp B.
Do đó \(X \subset A\) và \(X \subset B\).
Viết tập hợp X gồm những thành viên tham gia cả hai chuyên đề 1 và 2 trong tình huống mở đầu.
Tập X có phải là tập con của tập A không? Tập X có phải là tập con của tập B không? (A, B là các tập hợp trong HĐ1).
Lời giải chi tiết:

X = {Khánh; Bình; Hương; Chi; Tú}
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Dễ thấy: Các phần tử của X đều là phần tử của tập hợp A và tập hợp B.
Do đó \(X \subset A\) và \(X \subset B\).
Cho các tập hợp C = [1; 5], D = [-2; 3]. Hãy xác định tập hợp \(C \cap \;D\).
Lời giải chi tiết:
Ta có:

Giao của hai tập hợp C và D là \(C \cap \;D = \left[ {1;3} \right]\).
Trở lại tình huống mở đầu, hãy xác định tập hợp các thành viên tham gia Chuyên đề 1 hoặc Chuyên đề 2.
Lời giải chi tiết:
Kí hiệu H là tập hợp tất cả các thành viên tham gia chuyên đề 1 hoặc chuyên đề 2.
Tập hợp các bạn tham gia chuyên đề 1: A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
Tập hợp các bạn tham gia chuyên đề 2: B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Vậy H = {Nam; Ngân; Hân; Hiền; Lam; Khánh; Bình; Hương; Chi; Tú }
Chú ý khi giải
Mỗi phần tử chỉ liệt kê một lần.
Hãy biểu diễn tập hợp \(A \cup \;\,B\) bằng biểu đồ Ven, với A, B được cho trong HĐ1
Lời giải chi tiết:
Ta có:
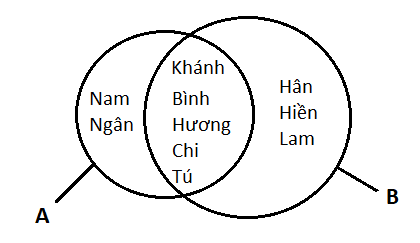
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Biểu đồ Ven
Trở lại tình huống mở đầu, hãy xác định tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2.
Lời giải chi tiết:
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
X = {Khánh; Bình; Hương; Chi; Tú }
Có Nam và Ngân chỉ tham gia chuyên đề 1.
Tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2 là
G = {Nam; Ngân}
Tìm phần bù của các tập hợp sau trong \(\mathbb{R}\):
a) \(\left( { - \infty ; - 2} \right)\)
b) \([ - 5; + \infty )\)
Phương pháp giải:
Biểu diễn các tập hợp trên trục số.
Lời giải chi tiết:
Ta có:

Suy ra phần bù của tập hợp \(\left( { - \infty ; - 2} \right)\) trong \(\mathbb{R}\) là: \(\mathbb{R}{\rm{\backslash }}\left( { - \infty ; - 2} \right) = [ - 2; + \infty )\)

Suy ra phần bù của tập hợp \([ - 5; + \infty )\) trong \(\mathbb{R}\) là: \(\mathbb{R}{\rm{\backslash }}[ - 5; + \infty ) = ( - \infty ; - 5)\)
Lớp 10A có 24 bạn tham gia thi đấu bóng đá và cầu lông, trong đó có 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông. Giả sử các trận bóng đá và cầu lông không tổ chức đồng thời. Hỏi có bao nhiêu bạn lớp 10A tham gia thi đấu cả bóng đá và cầu lông?
Phương pháp giải:
Gọi x là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Sử dụng biểu đồ Ven để mô tả các tập hợp.
Lời giải chi tiết:
Gọi \(x\) là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Ta có: 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông
\( \Rightarrow \) Có \(16 - x\) bạn chỉ tham gia thi đấu bóng đá mà không thi đấu cầu lông.
Và có \(11 - x\) bạn chỉ tham gia thi đấu cầu lông mà không thi đấu bóng đá.
Ta có biểu đồ Ven như sau:
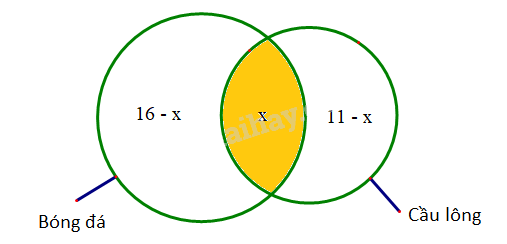
Tổng số bạn tham gia thi đấu bóng đá và cầu lông là: 16-x + x + 11-x = 24 => x=3.
Vậy lớp 10A có 3 bạn tham ggia thi đấu cả bóng đá và cầu lông.
Mục 3 trong SGK Toán 10 tập 1 - Kết nối tri thức tập trung vào các kiến thức cơ bản về tập hợp số thực, bao gồm các phép toán trên số thực, tính chất của các phép toán, và các ứng dụng của số thực trong thực tế. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia trên các số thực khác nhau. Để giải bài tập này, học sinh cần nắm vững các quy tắc về dấu của số thực, thứ tự thực hiện các phép toán, và các tính chất giao hoán, kết hợp, phân phối của các phép toán.
Bài tập này yêu cầu học sinh chứng minh các tính chất giao hoán, kết hợp, phân phối của các phép toán trên số thực. Để giải bài tập này, học sinh cần hiểu rõ định nghĩa của các tính chất này và biết cách áp dụng chúng vào các biểu thức cụ thể.
Bài tập này yêu cầu học sinh giải các bài toán thực tế liên quan đến số thực, ví dụ như tính tiền lãi, tính diện tích, tính thể tích. Để giải bài tập này, học sinh cần biết cách chuyển đổi các đơn vị đo lường, biết cách sử dụng các công thức tính toán, và biết cách phân tích bài toán để tìm ra lời giải.
| Số lượng | Giá mỗi đơn vị | Tổng giá trị |
|---|---|---|
| 5 | 10.000 VNĐ | 50.000 VNĐ |
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 3 trang 16, 17, 18 SGK Toán 10 tập 1 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức Toán học. Hãy truy cập website của chúng tôi để tìm hiểu thêm về các bài giải Toán 10 và các môn học khác.