Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Chúng tôi giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán trong sách giáo khoa.
Mục 2 trang 7 SGK Toán 10 tập 2 - Kết nối tri thức là một phần quan trọng trong chương trình học. Chúng tôi sẽ cung cấp cho bạn phương pháp giải bài tập hiệu quả và chính xác.
Quan sát Hình 6.2 và cho biết những điểm nào sau đây nằm trên đồ thị của hàm số a) Dựa vào đồ thị (H.6.2), tìm x sao cho y = 8 Nếu lượng điện tiêu thụ từ trên 50 đến 100 kWh (50 < x <= 100\)) thù công thức liên hệ giữa y và x đã thiết lập ở HĐ3 không còn đúng nữa.
a) Dựa vào đồ thị \(y = \frac{1}{2}{x^2}\) (H.6.2), tìm x sao cho \(y = 8\)
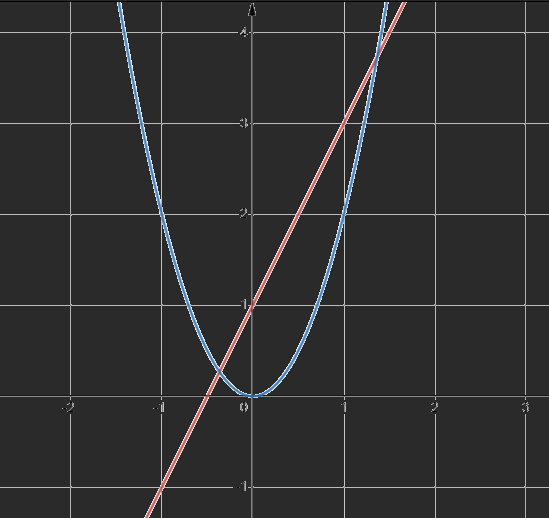
b) Vẽ đồ thị của các hàm số \(y = 2x + 1\) và \(y = 2{x^2}\) trên cùng một mặt phẳng tọa độ.
Lời giải chi tiết:
a) Để \(y = 8 \Leftrightarrow \frac{1}{2}{x^2} = 8 \Leftrightarrow {x^2} = 16 \Leftrightarrow x = 4\) hoăc \(x = - 4\)
b) Vẽ đồ thị y=2x+1:
-Là đồ thị bậc nhất nên đồ thị là đường thẳng đi qua điểm có tọa độ (0; 1) và
(-1; -1)
Vẽ đồ thị \(y = 2{x^2}\)
- Đi qua điểm (1; 2) ; (-1; 2);(0;0)
Nếu lượng điện tiêu thụ từ trên 50 đến 100 kWh (\(50 < x \le 100\)) thù công thức liên hệ giữa y và x đã thiết lập ở HĐ3 không còn đúng nữa.
Theo bảng giá bán lẻ điện sinh hoạt (Bảng 6.2) thì số tiền phải trả là:
\(y = 1,678.50 + 1,734(x - 50) = 83,9 + 1,734(x - 50)\), hay \(y = 1,734x - 2,8\)(nghìn đồng)
Vậy trên tập xác định \(D = (50;100{\rm{]}}\), hàm số y mô tả số tiền phải thanh toán có công thức là \(y = 1,734x - 2,8\); tập giá trị của nó là (83,9; 170,6].
Hãy vẽ đồ thị ở Hình 6.3 vào vở rồi vẽ tiếp đồ thị của hàm số \(y = 1,734x - 2,8\)trên tập \(D = (50;100{\rm{]}}\)
Lời giải chi tiết:
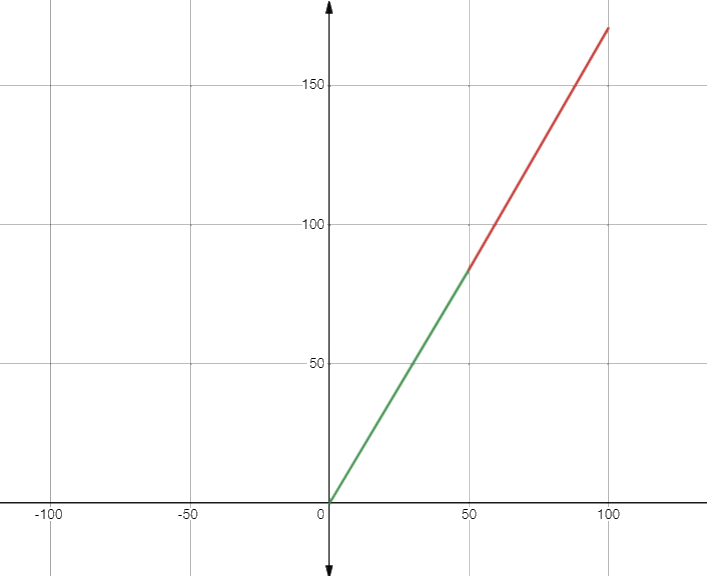
Vẽ đồ thị y =1,734x-2,8
- Là 1 đường thẳng đi qua điểm có tọa độ (55; 92,57) và (60;101,24)
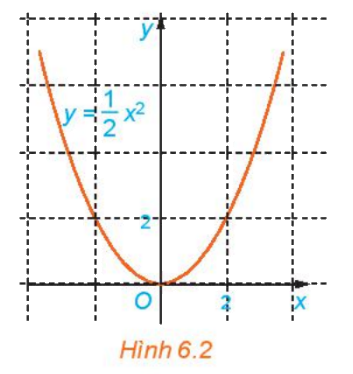
Quan sát Hình 6.2 và cho biết những điểm nào sau đây nằm trên đồ thị của hàm số \(y = \frac{1}{2}{x^2}\).
(0; 0), (2; 2), (-2; 2), (1; 2), (-1; 2).
Nêu nhận xét về mối quan hệ giữa hoành độ và tung độ của những điểm nằm trên đồ thị.
Lời giải chi tiết:
Dựa vào độ thị ta thấy (0; 0); (2; 2); (-2; 2) nằm trên đồ thị hàm số \(y = \frac{1}{2}{x^2}\)
Ta nhận ra được: \(\begin{array}{l}0 = \frac{1}{2}{.0^2}\\2 = \frac{1}{2}{.2^2}\\2 = \frac{1}{2}.{( - 2)^2}\end{array}\) Vì vậy những điểm có tọa độ \(\left( {x;\frac{1}{2}{x^2}} \right)\) sẽ nằm trên đồ thị.
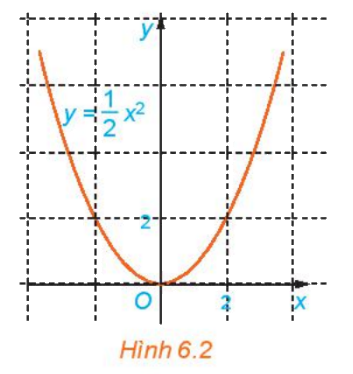
Quan sát Hình 6.2 và cho biết những điểm nào sau đây nằm trên đồ thị của hàm số \(y = \frac{1}{2}{x^2}\).
(0; 0), (2; 2), (-2; 2), (1; 2), (-1; 2).
Nêu nhận xét về mối quan hệ giữa hoành độ và tung độ của những điểm nằm trên đồ thị.
Lời giải chi tiết:
Dựa vào độ thị ta thấy (0; 0); (2; 2); (-2; 2) nằm trên đồ thị hàm số \(y = \frac{1}{2}{x^2}\)
Ta nhận ra được: \(\begin{array}{l}0 = \frac{1}{2}{.0^2}\\2 = \frac{1}{2}{.2^2}\\2 = \frac{1}{2}.{( - 2)^2}\end{array}\) Vì vậy những điểm có tọa độ \(\left( {x;\frac{1}{2}{x^2}} \right)\) sẽ nằm trên đồ thị.
a) Dựa vào đồ thị \(y = \frac{1}{2}{x^2}\) (H.6.2), tìm x sao cho \(y = 8\)
b) Vẽ đồ thị của các hàm số \(y = 2x + 1\) và \(y = 2{x^2}\) trên cùng một mặt phẳng tọa độ.
Lời giải chi tiết:
a) Để \(y = 8 \Leftrightarrow \frac{1}{2}{x^2} = 8 \Leftrightarrow {x^2} = 16 \Leftrightarrow x = 4\) hoăc \(x = - 4\)
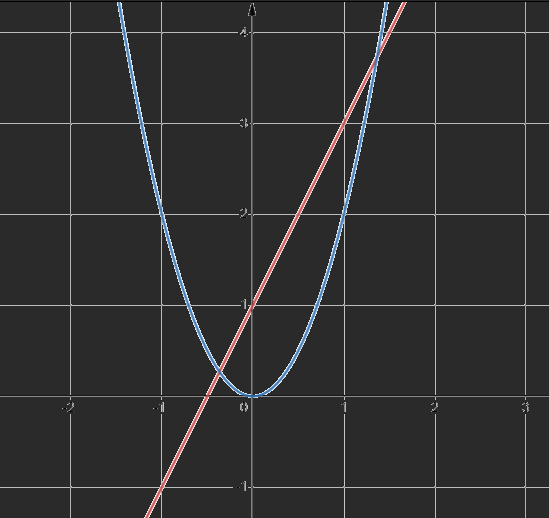
b) Vẽ đồ thị y=2x+1:
-Là đồ thị bậc nhất nên đồ thị là đường thẳng đi qua điểm có tọa độ (0; 1) và
(-1; -1)
Vẽ đồ thị \(y = 2{x^2}\)
- Đi qua điểm (1; 2) ; (-1; 2);(0;0)
Nếu lượng điện tiêu thụ từ trên 50 đến 100 kWh (\(50 < x \le 100\)) thù công thức liên hệ giữa y và x đã thiết lập ở HĐ3 không còn đúng nữa.
Theo bảng giá bán lẻ điện sinh hoạt (Bảng 6.2) thì số tiền phải trả là:
\(y = 1,678.50 + 1,734(x - 50) = 83,9 + 1,734(x - 50)\), hay \(y = 1,734x - 2,8\)(nghìn đồng)
Vậy trên tập xác định \(D = (50;100{\rm{]}}\), hàm số y mô tả số tiền phải thanh toán có công thức là \(y = 1,734x - 2,8\); tập giá trị của nó là (83,9; 170,6].
Hãy vẽ đồ thị ở Hình 6.3 vào vở rồi vẽ tiếp đồ thị của hàm số \(y = 1,734x - 2,8\)trên tập \(D = (50;100{\rm{]}}\)
Lời giải chi tiết:
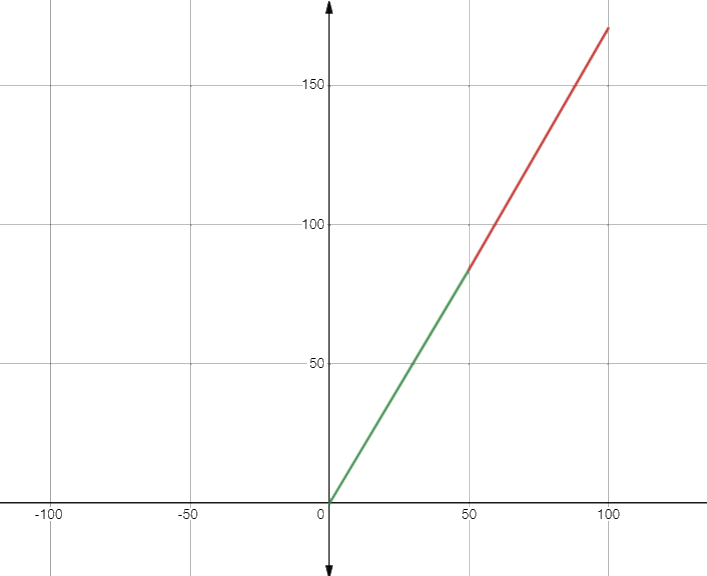
Vẽ đồ thị y =1,734x-2,8
- Là 1 đường thẳng đi qua điểm có tọa độ (55; 92,57) và (60;101,24)
Mục 2 trang 7 SGK Toán 10 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về vectơ. Cụ thể, các bài tập trong mục này thường xoay quanh các chủ đề như:
Để giải tốt các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc phép toán vectơ. Ngoài ra, việc rèn luyện kỹ năng vẽ hình và phân tích bài toán cũng rất quan trọng.
Bài 1 yêu cầu học sinh tìm vectơ chỉ phương của đường thẳng. Để làm được bài này, học sinh cần hiểu rõ khái niệm vectơ chỉ phương và cách xác định vectơ chỉ phương từ phương trình đường thẳng.
Ví dụ, cho đường thẳng có phương trình 2x + 3y - 1 = 0. Để tìm vectơ chỉ phương của đường thẳng này, ta có thể làm như sau:
Trong trường hợp này, a = 2, b = 3, c = -1. Vậy vectơ chỉ phương của đường thẳng là (3, -2).
Bài 2 yêu cầu học sinh xác định vị trí tương đối của hai đường thẳng. Để làm được bài này, học sinh cần hiểu rõ các trường hợp vị trí tương đối của hai đường thẳng: song song, cắt nhau, trùng nhau.
Để xác định vị trí tương đối của hai đường thẳng, ta có thể sử dụng các phương pháp sau:
Bài 3 yêu cầu học sinh tìm giao điểm của hai đường thẳng. Để làm được bài này, học sinh cần giải hệ phương trình gồm phương trình của hai đường thẳng.
Ví dụ, cho hai đường thẳng có phương trình:
Để tìm giao điểm của hai đường thẳng này, ta giải hệ phương trình sau:
| 2x + y = 5 | x - y = 1 | |
|---|---|---|
| Cộng hai phương trình | 3x = 6 | |
| Giải phương trình | x = 2 | |
| Thay x = 2 vào phương trình x - y = 1 | 2 - y = 1 | |
| Giải phương trình | y = 1 |
Vậy giao điểm của hai đường thẳng là (2, 1).
Hy vọng với những hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết các bài tập trong mục 2 trang 7 SGK Toán 10 tập 2 - Kết nối tri thức. Chúc bạn học tốt!