Chào mừng bạn đến với bài học lý thuyết về các khái niệm mở đầu trong Toán học tại giaitoan.edu.vn! Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản nhất, là nền tảng để bạn có thể tiếp thu và giải quyết các bài toán phức tạp hơn trong tương lai.
Chúng ta sẽ cùng nhau khám phá các khái niệm như tập hợp, số tự nhiên, số nguyên, phép toán cơ bản và các tính chất quan trọng của chúng.
1. KHÁI NIỆM VECTƠ 2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU
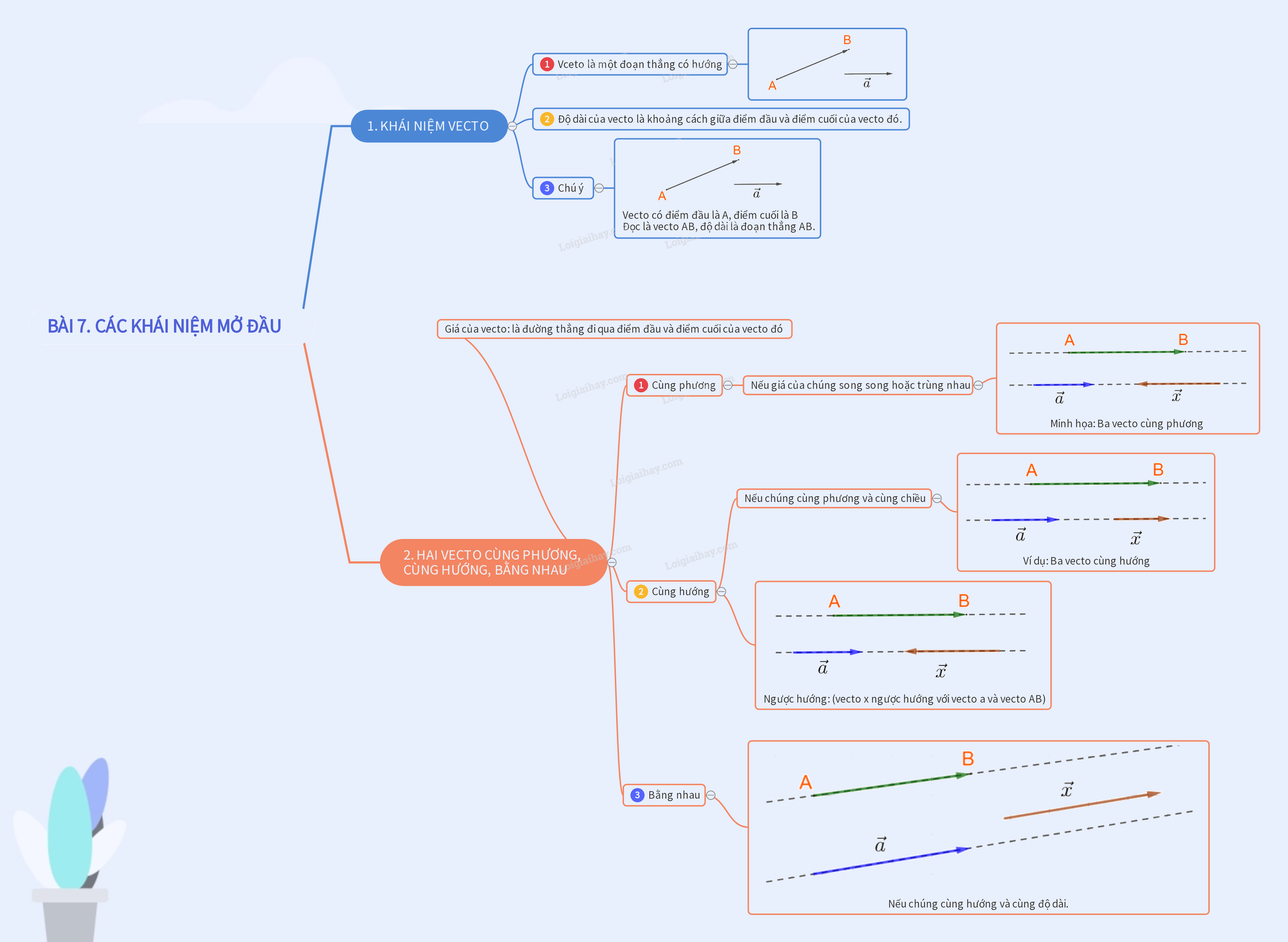
1. KHÁI NIỆM VECTƠ
+) Vectolà một đoạn thẳng có hướng.
Ví dụ 1: i) vecto \(\overrightarrow {AB} \): (đọc là vecto AB) 
ii) Vecto \(\overrightarrow {BA} \): 
iii) vecto \(\overrightarrow u \): 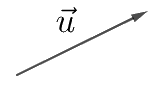
+) Độ dài của vecto là khoảng cách giữa điểm đầu và điểm cuối của vecto đó.
Kí hiệu: độ dài của vecto \(\overrightarrow {AB} \) là \(\left| {\overrightarrow {AB} } \right|\).
Ví dụ 2: \(\left| {\overrightarrow {AB} } \right| = AB;\;\left| {\overrightarrow {DE} } \right| = DE\)
+) Vecto không, là vecto có độ dài bằng 0. Ví dụ: \(\overrightarrow {AA} ,\;\overrightarrow {EE} ,...\)(điểm đầu trùng điểm cuối)
Kí hiệu chung là \(\overrightarrow 0 \).
2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU
+) Giácủa vecto: là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.
Ví dụ: Giá của vecto \(\overrightarrow {CD} \) là đường thẳng CD
+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.
Ví dụ:
Ba vecto \(\overrightarrow u ,\;\overrightarrow {CD} ,\;\overrightarrow {AB} \) cùng phương.
Trong đó 2 vecto \(\overrightarrow u ,\;\overrightarrow {CD} \) cùng hướng, còn 2 vecto \(\overrightarrow {CD} ,\;\overrightarrow {AB} \) ngược hướng.
+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.
* Chú ý:
- Chỉ khi hai vecto cùng phương ta mới nói tới chúng cùng hướng hay ngược hướng.
- Vecto \(\overrightarrow 0 \) cùng phương, cùng hướng với mọi vecto.
- Với mỗi điểm O và vecto \(\overrightarrow a \) cho trước, có duy nhất điểm A sao cho \(\overrightarrow {OA} = \overrightarrow a \)
* Nhận xét:
+) Ba điểm A, B, C thẳng hàng khi và chỉ khi \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương.
+) Ba điểm A, B, C thẳng hàng, B nằm giữa khi và chỉ khi \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng.
Toán học là môn khoa học nghiên cứu về số lượng, cấu trúc, không gian và sự thay đổi. Để bắt đầu hành trình khám phá thế giới Toán học, việc nắm vững các khái niệm mở đầu là vô cùng quan trọng. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về các khái niệm cơ bản này.
Tập hợp là một khái niệm nền tảng trong Toán học. Một tập hợp là một bộ sưu tập các đối tượng được xác định rõ ràng, được gọi là các phần tử của tập hợp. Tập hợp có thể chứa bất kỳ loại đối tượng nào, chẳng hạn như số, chữ cái, người, hoặc thậm chí các tập hợp khác.
Ví dụ:
Số tự nhiên là các số dùng để đếm. Tập hợp các số tự nhiên được ký hiệu là ℕ = {0, 1, 2, 3, ...}. Số tự nhiên được sử dụng để biểu diễn số lượng đối tượng, thứ tự, và nhiều khái niệm khác trong cuộc sống.
Các tính chất của số tự nhiên:
Số nguyên là tập hợp các số bao gồm số tự nhiên, số âm và số 0. Tập hợp các số nguyên được ký hiệu là ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}. Số nguyên được sử dụng để biểu diễn các giá trị có thể âm hoặc dương.
Các tính chất của số nguyên:
Các phép toán cơ bản trong Toán học bao gồm:
Các tính chất của phép toán:
Ngoài các tính chất của phép toán, còn có một số tính chất quan trọng khác cần lưu ý:
Các khái niệm mở đầu này có ứng dụng rộng rãi trong cuộc sống hàng ngày và trong các lĩnh vực khác của Toán học. Ví dụ:
Việc nắm vững các khái niệm mở đầu này là bước đầu tiên quan trọng để bạn có thể tiếp thu và giải quyết các bài toán phức tạp hơn trong Toán học. Hãy luyện tập thường xuyên và áp dụng các kiến thức này vào thực tế để hiểu rõ hơn về thế giới Toán học.