Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 4, trang 41 và 42 của sách giáo khoa Toán 10 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho tam giác ABC với I là tâm đường trong nội tiếp tam giác Cho tam giác ABC với đường cao BD. a) Biểu thị BD theo AB và sinA. Tính diện tích tam giác ABC có b = 2, B = 30, C = 45 Ta đã biết tính cos A theo độ dài các cạnh của tam giác ABC. Liệu sin A và diện tích S có tính theo độ dài các cạnh của tam giác ABC hay không? Công viên Hòa Bình (Hà Nội) có dạng hình ngũ giác ABCDE như hình 3.17
Tính diện tích tam giác ABC có \(b = 2,\;\widehat B = {30^o},\;\widehat C = {45^o}\).
Phương pháp giải:
\(S = \frac{1}{2}bc.\sin A.\)
Bước 1: Tính c bằng cách áp dụng định lí sin.
Bước 2: Tính góc \(\;\widehat A\), tính \(S = \frac{1}{2}bc.\sin A.\)
Lời giải chi tiết:
Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
\( \Rightarrow c = \sin C.\frac{b}{{\sin B}} = \sin {45^o}.\frac{2}{{\sin {{30}^o}}} = 2\sqrt 2 \)
Lại có: \(\;\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {30^o} - {45^o} = {105^o}\)
Do đó diện tích tích S của tam giác ABC là:
\(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.2.2\sqrt 2 .\sin {105^o} = 1 + \sqrt 3 .\)
Vậy diện tích tam giác ABC là \(1 + \sqrt 3 \).
Ta đã biết tính cos A theo độ dài các cạnh của tam giác ABC. Liệu sin A và diện tích S có tính theo độ dài các cạnh của tam giác ABC hay không?
Phương pháp giải:
Nhắc lại:
+) công thức tính diện tích tam giác ABC: \(S = \frac{1}{2}bc.\sin A.\)
+) \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Bước 1: Tính sin A theo cos A. Lưu ý: \(\sin A > 0\)
Bước 2: Thay sin A vào \(S = \frac{1}{2}bc.\sin A.\) Rút gọn biểu thức rồi kết luận.
Lời giải chi tiết:
Từ định lí cosin trong tam giác ABC, ta suy ra: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \({\sin ^2}A + {\cos ^2}A = 1\)
\( \Rightarrow \sin A = \pm \sqrt {1 - {{\cos }^2}A} \)
Do \({0^o} < \widehat A < {180^o}\) nên \(\sin A > 0\) hay \(\sin A = \sqrt {1 - {{\cos }^2}A} \)
Ta có:
\(\begin{array}{l}\sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}} = \sqrt {1 - \frac{{{{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}} \\ = \sqrt {\frac{{4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}} = \frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}}\end{array}\)
Thế vào công thức tính diện tích tam giác ABC ta được:
\(S = \frac{1}{2}bc.\frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}} = \frac{1}{4}.\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} \)
Chú ý:
Nếu tiếp tục biến đổi công thức diện tích ta được
\(\begin{array}{l}S = \frac{1}{4}.\sqrt {\left( {2bc + {b^2} + {c^2} - {a^2}} \right)\left( {2bc - {b^2} - {c^2} + {a^2}} \right)} \\ = \frac{1}{4}.\sqrt {\left[ {{{\left( {b + c} \right)}^2} - {a^2}} \right]\left[ {{a^2} - {{\left( {b - c} \right)}^2}} \right]} \\ = \frac{1}{4}.\sqrt {\left( {b + c - a} \right)\left( {b + c + a} \right)\left( {a - b + c} \right)\left( {a + b - c} \right)} \end{array}\)
Đến đây, đặt \(p = \frac{{a + b + c}}{2}\), là nửa chu vi tam giác ABC, ta suy ra:
\(\left\{ \begin{array}{l}b + c + a = 2p\\b + c - a = b + c + a - 2a = 2\left( {p - a} \right)\\a - b + c = b + c + a - 2b = 2\left( {p - b} \right)\\a + b - c = b + c + a - 2c = 2\left( {p - c} \right)\end{array} \right.\)
\(\begin{array}{l} \Rightarrow S = \frac{1}{4}\sqrt {2\left( {p - a} \right).2p.2\left( {p - b} \right).2\left( {p - c} \right)} \\ \Leftrightarrow S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \end{array}\)
(công thức Heron)
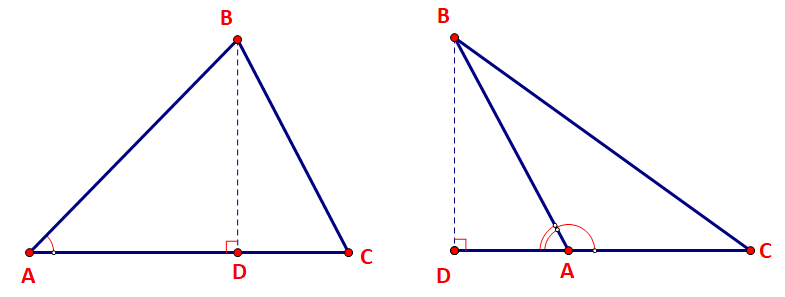
Cho tam giác ABC với đường cao BD.
a) Biểu thị BD theo AB và sinA.
b) Viết công thức tính diện tích S của tam giác ABC theo b,c, sin A.
Phương pháp giải:
a) Biểu thị BD dựa vào sin A (hoặc \(\sin \left( {{{180}^o} - {\rm{ }}A} \right)\)) trong tam giác vuông ABD.
b)
+) Tính \({S_{ABC}} = \frac{1}{2}BD.AC\)
+) Thay BD ở ý a) để suy ra công thức tính S theo b,c và sin A.
Lời giải chi tiết:
a) Xét tam giác vuông ABD vuông tại D ta có:
TH1: góc A nhọn
\(\sin A = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)
TH2: góc A tù
\(\sin A = \sin ({180^o} - A) = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)
Vậy \(BD = AB.\sin A\)
b) Ta có diện tích S của tam giác ABC là: \(S = \frac{1}{2}BD.AC\)
Mà \(BD = AB.\sin A = c.\sin A\); BC = a. Thế vào (*) ta được:
\(S = \frac{1}{2}c.\sin A.b\) hay \(S = \frac{1}{2}bc.\sin A.\)
Vậy diện tích S của tam giác ABC theo b, c, sin A là \(S = \frac{1}{2}bc.\sin A.\)
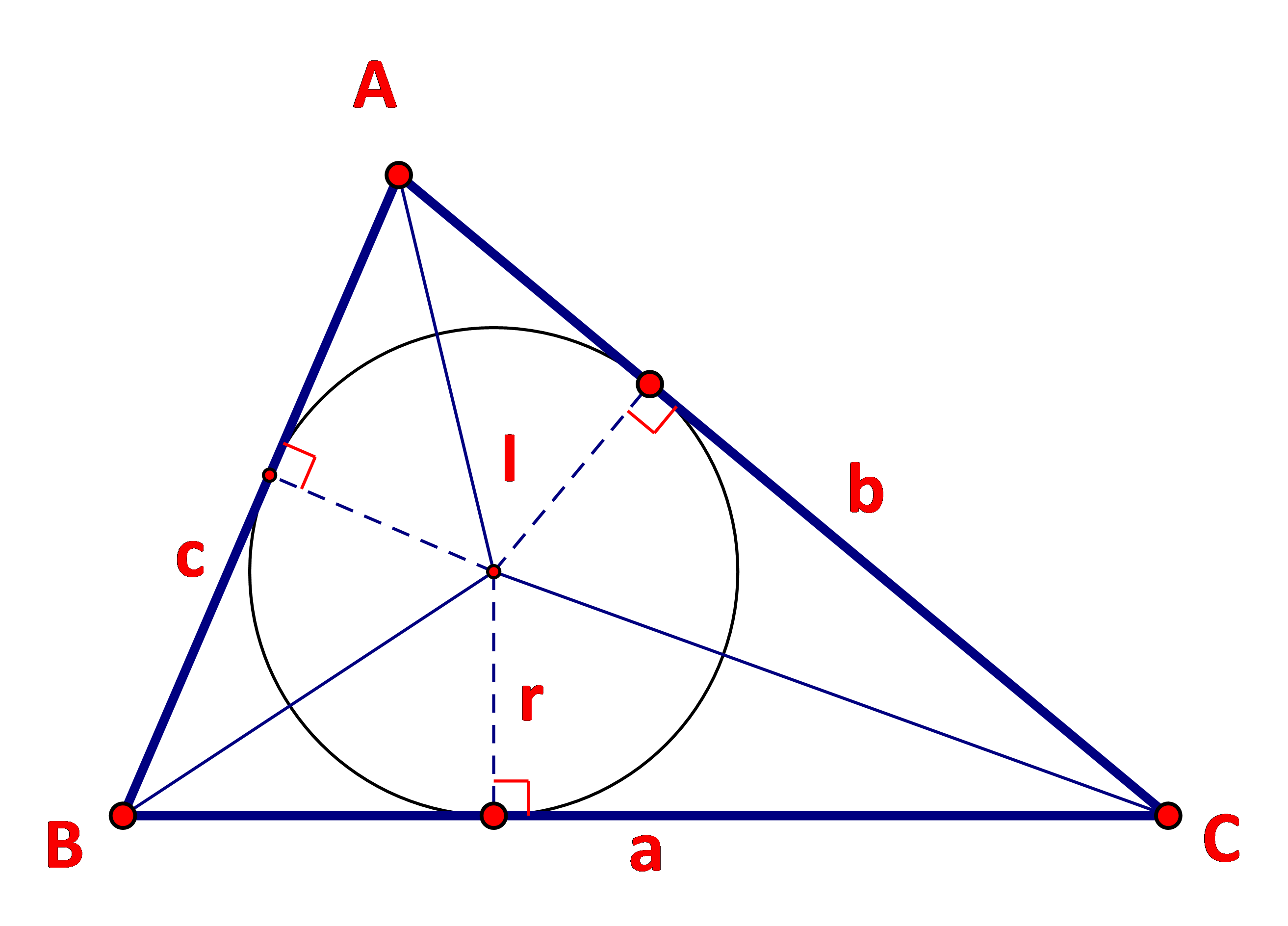
Cho tam giác ABC với I là tâm đường trong nội tiếp tam giác.
a) Nêu mối liên hệ giữa diện tích tam giác ABC và diện tích các tam giác IBC, ICA, IAB.
b) Tính diện tích tam giác ABC theo r,a,b,c.
Phương pháp giải:
a) Tính diện tích tam giác ABC theo diện tích các tam giác IBC, ICA, IAB.
b) Diện tích tam giác IBC: \({S_{IBC}} = \frac{1}{2}r.a\).
Lời giải chi tiết:
a) Diện tích tam giác ABC là: \[S = {S_{IAB}} + {S_{IBC}} + {S_{IAC}}\]
b)
Kí hiệu: D,E, F lần lượt là hình chiếu của I trên AB, BC, AC.
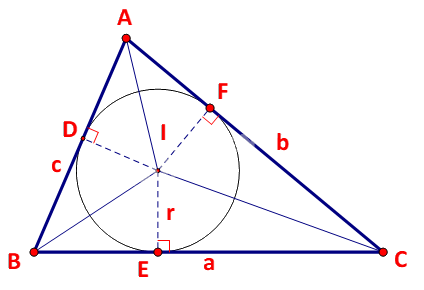
Ta có:
\(\begin{array}{l}{S_{IAB}} = \frac{1}{2}.ID.AB = \frac{1}{2}r.c\\{S_{IBC}} = \frac{1}{2}IE.BC = \frac{1}{2}r.a\\{S_{IAC}} = \frac{1}{2}IF.AC = \frac{1}{2}r.b\end{array}\)
\( \Rightarrow S = \frac{1}{2}r.c + \frac{1}{2}r.a + \frac{1}{2}r.b = \frac{1}{2}r.\left( {a + b + c} \right)\)
Vậy diện tích tam giác ABC tính theo r, a, b, c là \(S = \frac{1}{2}r.\left( {a + b + c} \right)\).
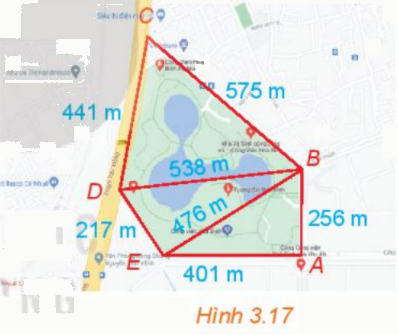
Công viên Hòa Bình (Hà Nội) có dạng hình ngũ giác ABCDE như hình 3.17. Dùng chế dộ tình khoảng cách giữa hai điểm của Google Maps, một người xác định được các khoảng cách như trong hình vẽ. Theo số liệu đó, em hãy tính diện tích của công viên hòa bình.
Phương pháp giải:
Bước 1: Tính diện tích các tam giác CBD, DBE, EBA bằng công thức Herong:
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)
Bước 2: Tính diện tích ngũ giác ABCDE, bằng tổng diện tích các tam giác CBD, DBE, EBA.
Lời giải chi tiết:
Xét tam giác CDB, ta có: CD = 441, CB = 575 và DB = 538 (đơn vị: m)
Và nửa chu vi là: \(\frac{{441 + 575 + 538}}{2} = 777(m)\)
Do đó: \({S_{CDB}} = \sqrt {777.\left( {777 - 441} \right).\left( {777 - 575} \right).\left( {777 - 538} \right)} \approx 112267,7\left( {{m^2}} \right)\)
Xét tam giác DBE, ta có: DE = 217, EB = 476 và DB = 538 (đơn vị: m)
Và nửa chu vi là: \(\frac{{217 + 476 + 538}}{2} = 615,5(m)\)
Do đó: \({S_{DBE}} = \sqrt {615,5.\left( {615,5 - 217} \right).\left( {615,5 - 476} \right).\left( {615,5 - 538} \right)} \approx 51495,13\left( {{m^2}} \right)\)
Xét tam giác ABE, ta có: AE = 401, EB = 476 và BA =256 (đơn vị: m)
Và nửa chu vi là: \(\frac{{401 + 476 + 256}}{2} = 566,5(m)\)
Do đó: \({S_{ABE}} = \sqrt {566,5.\left( {566,5 - 401} \right).\left( {566,5 - 476} \right).\left( {566,5 - 256} \right)} \approx 51327,97\left( {{m^2}} \right)\)
Vậy diện tích S của ngũ giác ABCDE là: \(S = {S_{CDB}} + {S_{DBE}} + {S_{ABE}} \approx 112267,7 + 51495,13 + 51327,97 = 215090,8\left( {{m^2}} \right)\)
Chú ý
+) Để tính diện tích ngũ giác ABCDE thông qua các tam giác nhỏ, ta cần chọn các tam giác thỏa mãn: “phần trong của chúng không đè lên nhau” và “ghép lại vừa khít tạo thành ngũ giác ABCDE”
+) Ưu tiên tính thông qua các tam giác đã biết đủ các cạnh.
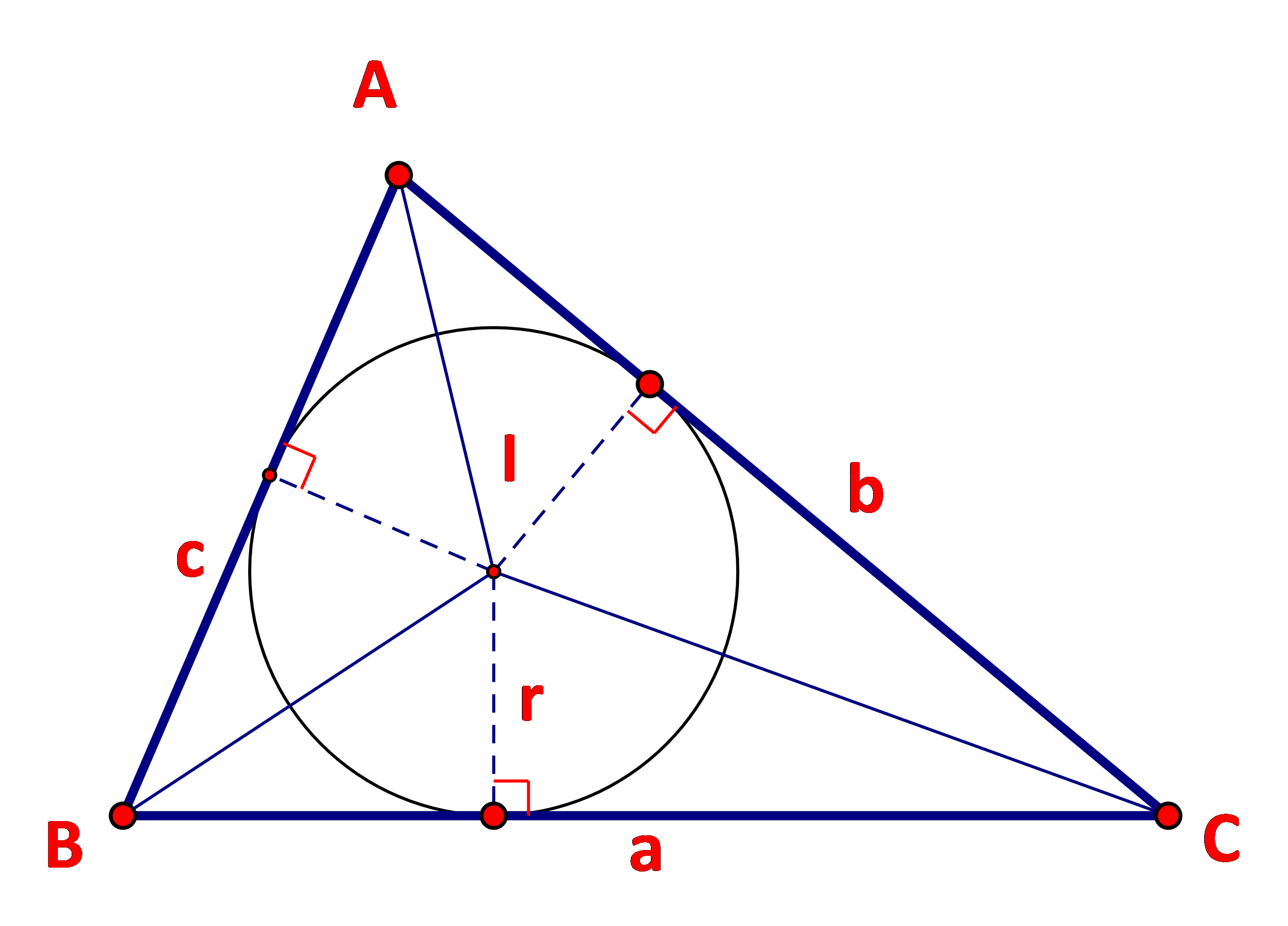
Cho tam giác ABC với I là tâm đường trong nội tiếp tam giác.
a) Nêu mối liên hệ giữa diện tích tam giác ABC và diện tích các tam giác IBC, ICA, IAB.
b) Tính diện tích tam giác ABC theo r,a,b,c.
Phương pháp giải:
a) Tính diện tích tam giác ABC theo diện tích các tam giác IBC, ICA, IAB.
b) Diện tích tam giác IBC: \({S_{IBC}} = \frac{1}{2}r.a\).
Lời giải chi tiết:
a) Diện tích tam giác ABC là: \[S = {S_{IAB}} + {S_{IBC}} + {S_{IAC}}\]
b)
Kí hiệu: D,E, F lần lượt là hình chiếu của I trên AB, BC, AC.
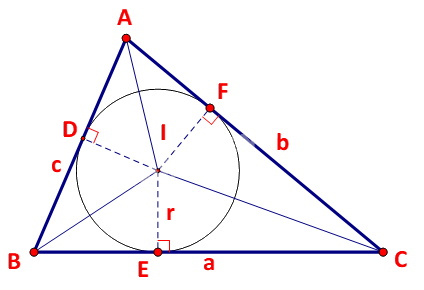
Ta có:
\(\begin{array}{l}{S_{IAB}} = \frac{1}{2}.ID.AB = \frac{1}{2}r.c\\{S_{IBC}} = \frac{1}{2}IE.BC = \frac{1}{2}r.a\\{S_{IAC}} = \frac{1}{2}IF.AC = \frac{1}{2}r.b\end{array}\)
\( \Rightarrow S = \frac{1}{2}r.c + \frac{1}{2}r.a + \frac{1}{2}r.b = \frac{1}{2}r.\left( {a + b + c} \right)\)
Vậy diện tích tam giác ABC tính theo r, a, b, c là \(S = \frac{1}{2}r.\left( {a + b + c} \right)\).
Cho tam giác ABC với đường cao BD.
a) Biểu thị BD theo AB và sinA.
b) Viết công thức tính diện tích S của tam giác ABC theo b,c, sin A.
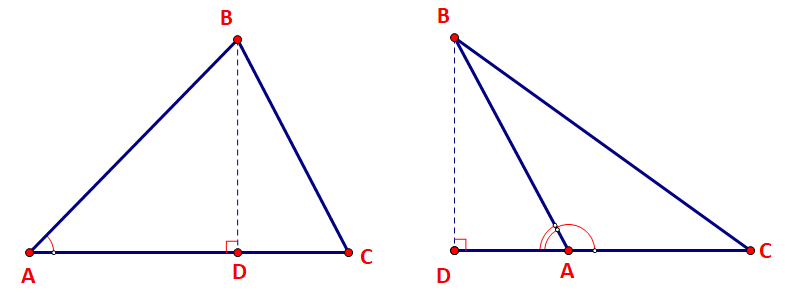
Phương pháp giải:
a) Biểu thị BD dựa vào sin A (hoặc \(\sin \left( {{{180}^o} - {\rm{ }}A} \right)\)) trong tam giác vuông ABD.
b)
+) Tính \({S_{ABC}} = \frac{1}{2}BD.AC\)
+) Thay BD ở ý a) để suy ra công thức tính S theo b,c và sin A.
Lời giải chi tiết:
a) Xét tam giác vuông ABD vuông tại D ta có:
TH1: góc A nhọn
\(\sin A = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)
TH2: góc A tù
\(\sin A = \sin ({180^o} - A) = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)
Vậy \(BD = AB.\sin A\)
b) Ta có diện tích S của tam giác ABC là: \(S = \frac{1}{2}BD.AC\)
Mà \(BD = AB.\sin A = c.\sin A\); BC = a. Thế vào (*) ta được:
\(S = \frac{1}{2}c.\sin A.b\) hay \(S = \frac{1}{2}bc.\sin A.\)
Vậy diện tích S của tam giác ABC theo b, c, sin A là \(S = \frac{1}{2}bc.\sin A.\)
Tính diện tích tam giác ABC có \(b = 2,\;\widehat B = {30^o},\;\widehat C = {45^o}\).
Phương pháp giải:
\(S = \frac{1}{2}bc.\sin A.\)
Bước 1: Tính c bằng cách áp dụng định lí sin.
Bước 2: Tính góc \(\;\widehat A\), tính \(S = \frac{1}{2}bc.\sin A.\)
Lời giải chi tiết:
Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
\( \Rightarrow c = \sin C.\frac{b}{{\sin B}} = \sin {45^o}.\frac{2}{{\sin {{30}^o}}} = 2\sqrt 2 \)
Lại có: \(\;\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {30^o} - {45^o} = {105^o}\)
Do đó diện tích tích S của tam giác ABC là:
\(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.2.2\sqrt 2 .\sin {105^o} = 1 + \sqrt 3 .\)
Vậy diện tích tam giác ABC là \(1 + \sqrt 3 \).
Ta đã biết tính cos A theo độ dài các cạnh của tam giác ABC. Liệu sin A và diện tích S có tính theo độ dài các cạnh của tam giác ABC hay không?
Phương pháp giải:
Nhắc lại:
+) công thức tính diện tích tam giác ABC: \(S = \frac{1}{2}bc.\sin A.\)
+) \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Bước 1: Tính sin A theo cos A. Lưu ý: \(\sin A > 0\)
Bước 2: Thay sin A vào \(S = \frac{1}{2}bc.\sin A.\) Rút gọn biểu thức rồi kết luận.
Lời giải chi tiết:
Từ định lí cosin trong tam giác ABC, ta suy ra: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \({\sin ^2}A + {\cos ^2}A = 1\)
\( \Rightarrow \sin A = \pm \sqrt {1 - {{\cos }^2}A} \)
Do \({0^o} < \widehat A < {180^o}\) nên \(\sin A > 0\) hay \(\sin A = \sqrt {1 - {{\cos }^2}A} \)
Ta có:
\(\begin{array}{l}\sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}} = \sqrt {1 - \frac{{{{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}} \\ = \sqrt {\frac{{4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}} = \frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}}\end{array}\)
Thế vào công thức tính diện tích tam giác ABC ta được:
\(S = \frac{1}{2}bc.\frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}} = \frac{1}{4}.\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} \)
Chú ý:
Nếu tiếp tục biến đổi công thức diện tích ta được
\(\begin{array}{l}S = \frac{1}{4}.\sqrt {\left( {2bc + {b^2} + {c^2} - {a^2}} \right)\left( {2bc - {b^2} - {c^2} + {a^2}} \right)} \\ = \frac{1}{4}.\sqrt {\left[ {{{\left( {b + c} \right)}^2} - {a^2}} \right]\left[ {{a^2} - {{\left( {b - c} \right)}^2}} \right]} \\ = \frac{1}{4}.\sqrt {\left( {b + c - a} \right)\left( {b + c + a} \right)\left( {a - b + c} \right)\left( {a + b - c} \right)} \end{array}\)
Đến đây, đặt \(p = \frac{{a + b + c}}{2}\), là nửa chu vi tam giác ABC, ta suy ra:
\(\left\{ \begin{array}{l}b + c + a = 2p\\b + c - a = b + c + a - 2a = 2\left( {p - a} \right)\\a - b + c = b + c + a - 2b = 2\left( {p - b} \right)\\a + b - c = b + c + a - 2c = 2\left( {p - c} \right)\end{array} \right.\)
\(\begin{array}{l} \Rightarrow S = \frac{1}{4}\sqrt {2\left( {p - a} \right).2p.2\left( {p - b} \right).2\left( {p - c} \right)} \\ \Leftrightarrow S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \end{array}\)
(công thức Heron)
Công viên Hòa Bình (Hà Nội) có dạng hình ngũ giác ABCDE như hình 3.17. Dùng chế dộ tình khoảng cách giữa hai điểm của Google Maps, một người xác định được các khoảng cách như trong hình vẽ. Theo số liệu đó, em hãy tính diện tích của công viên hòa bình.
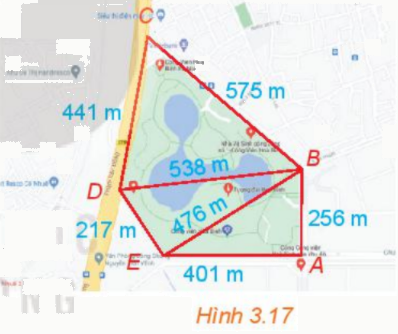
Phương pháp giải:
Bước 1: Tính diện tích các tam giác CBD, DBE, EBA bằng công thức Herong:
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)
Bước 2: Tính diện tích ngũ giác ABCDE, bằng tổng diện tích các tam giác CBD, DBE, EBA.
Lời giải chi tiết:
Xét tam giác CDB, ta có: CD = 441, CB = 575 và DB = 538 (đơn vị: m)
Và nửa chu vi là: \(\frac{{441 + 575 + 538}}{2} = 777(m)\)
Do đó: \({S_{CDB}} = \sqrt {777.\left( {777 - 441} \right).\left( {777 - 575} \right).\left( {777 - 538} \right)} \approx 112267,7\left( {{m^2}} \right)\)
Xét tam giác DBE, ta có: DE = 217, EB = 476 và DB = 538 (đơn vị: m)
Và nửa chu vi là: \(\frac{{217 + 476 + 538}}{2} = 615,5(m)\)
Do đó: \({S_{DBE}} = \sqrt {615,5.\left( {615,5 - 217} \right).\left( {615,5 - 476} \right).\left( {615,5 - 538} \right)} \approx 51495,13\left( {{m^2}} \right)\)
Xét tam giác ABE, ta có: AE = 401, EB = 476 và BA =256 (đơn vị: m)
Và nửa chu vi là: \(\frac{{401 + 476 + 256}}{2} = 566,5(m)\)
Do đó: \({S_{ABE}} = \sqrt {566,5.\left( {566,5 - 401} \right).\left( {566,5 - 476} \right).\left( {566,5 - 256} \right)} \approx 51327,97\left( {{m^2}} \right)\)
Vậy diện tích S của ngũ giác ABCDE là: \(S = {S_{CDB}} + {S_{DBE}} + {S_{ABE}} \approx 112267,7 + 51495,13 + 51327,97 = 215090,8\left( {{m^2}} \right)\)
Chú ý
+) Để tính diện tích ngũ giác ABCDE thông qua các tam giác nhỏ, ta cần chọn các tam giác thỏa mãn: “phần trong của chúng không đè lên nhau” và “ghép lại vừa khít tạo thành ngũ giác ABCDE”
+) Ưu tiên tính thông qua các tam giác đã biết đủ các cạnh.
Mục 4 của chương trình Toán 10 tập 1 - Kết nối tri thức tập trung vào các khái niệm và ứng dụng của vectơ trong mặt phẳng. Các bài tập trang 41 và 42 SGK Toán 10 tập 1 yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học và đại số. Việc nắm vững các định nghĩa, tính chất và phép toán vectơ là rất quan trọng để giải quyết thành công các bài tập này.
Bài tập này yêu cầu học sinh tìm tọa độ của một vectơ dựa trên tọa độ của các điểm đầu và điểm cuối của vectơ đó. Để giải bài tập này, học sinh cần nắm vững công thức tính tọa độ của vectơ: Nếu A(xA, yA) và B(xB, yB) thì vectơ AB có tọa độ là (xB - xA, yB - yA).
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân với một số thực trên các vectơ. Để giải bài tập này, học sinh cần nắm vững các quy tắc thực hiện các phép toán vectơ:
Bài tập này yêu cầu học sinh chứng minh một đẳng thức vectơ. Để giải bài tập này, học sinh cần sử dụng các tính chất của phép toán vectơ và các quy tắc biến đổi vectơ để đưa đẳng thức về dạng đơn giản nhất.
Bài tập này yêu cầu học sinh sử dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học, chẳng hạn như chứng minh hai đường thẳng song song, vuông góc, hoặc tìm tọa độ của một điểm.
Ví dụ: Cho A(1, 2) và B(3, 4). Tìm tọa độ của vectơ AB.
Giải: Tọa độ của vectơ AB là (3 - 1, 4 - 2) = (2, 2).
Khi giải bài tập về vectơ, cần chú ý đến dấu của tọa độ và các quy tắc biến đổi vectơ. Ngoài ra, việc vẽ hình minh họa sẽ giúp học sinh hiểu rõ hơn về bài toán và tìm ra hướng giải quyết hiệu quả.
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 4 trang 41, 42 SGK Toán 10 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!