Chào mừng bạn đến với bài học lý thuyết Phương trình quy về phương trình bậc hai trong chương trình Toán 10 Kết nối tri thức. Đây là một phần kiến thức quan trọng, giúp bạn xây dựng nền tảng vững chắc cho các bài toán phức tạp hơn về phương trình sau này.
Chúng tôi sẽ cung cấp một cách tiếp cận rõ ràng, dễ hiểu về các khái niệm, định lý và phương pháp giải quyết các phương trình đặc biệt này. Hãy cùng giaitoan.edu.vn khám phá!
A. Lý thuyết 1. Phương trình dạng \(\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \)
A. Lý thuyết
1. Phương trình dạng \(\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \)
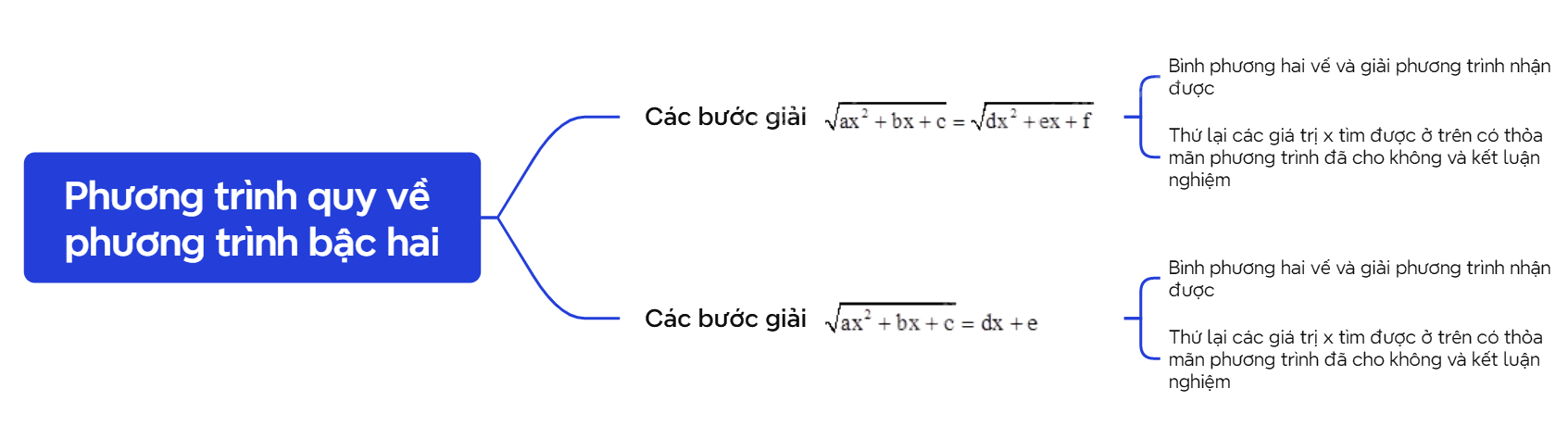
Để giải phương trình \(\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \), ta thực hiện như sau: - Bình phương hai vế và giải phương trình nhận được. - Thứ lại các giá trị x tìm được ở trên có thỏa mãn phương trình đã cho không và kết luận nghiệm. |
2. Phương trình dạng \(\sqrt {a{x^2} + bx + c} = dx + e\)
Để giải phương trình \(\sqrt {a{x^2} + bx + c} = dx + e\), ta thực hiện như sau: - Bình phương hai vế và giải phương trình nhận được. - Thứ lại các giá trị x tìm được ở trên có thỏa mãn phương trình đã cho không và kết luận nghiệm. |
B. Bài tập
Bài 1: Giải phương trình \(\sqrt {2{x^2} - 4x - 2} = \sqrt {{x^2} - x - 2} \).
Giải:
Bình phương hai vế của phương trình, ta được \(2{x^2} - 4 - 2 = {x^2} - x - 2\).
Sau khi thu gọn, ta được \({x^2} - 3x = 0\). Từ đó tìm được x = 0 hoặc x = 3.
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta chỉ thấy có x = 3 thỏa mãn.
Vậy nghiệm của phương trình đã cho là x = 3.
Bài 2: Giải phương trình \(\sqrt {2{x^2} - 5x - 9} = x - 1\).
Giải:
Bình phương hai vế của phương trình, ta được \(2{x^2} - 5x - 9 = {x^2} - 2x + 1\).
Sau khi thu gọn, ta được \({x^2} - 3x - 10 = 0\). Từ đó tìm được x = -2 hoặc x = 5.
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta chỉ thấy có x = 5 thỏa mãn.
Vậy nghiệm của phương trình đã cho là x = 5.

Trong chương trình Toán 10 Kết nối tri thức, phương trình quy về phương trình bậc hai đóng vai trò quan trọng trong việc rèn luyện kỹ năng giải toán và tư duy logic. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết này, bao gồm định nghĩa, các dạng phương trình thường gặp, và phương pháp giải.
Phương trình quy về phương trình bậc hai là phương trình có thể được biến đổi về dạng ax2 + bx + c = 0, với a ≠ 0. Các dạng phương trình thường gặp bao gồm:
Để giải các phương trình này, chúng ta thường thực hiện các bước sau:
Ví dụ 1: Giải phương trình (x - 2)(x + 3) = 0
Phương trình tích này có hai nghiệm: x = 2 và x = -3.
Ví dụ 2: Giải phương trình √(2x + 1) = x - 1
Bước 1: Bình phương hai vế: 2x + 1 = (x - 1)2
Bước 2: Khai triển và biến đổi về dạng bậc hai: x2 - 4x = 0
Bước 3: Giải phương trình bậc hai: x(x - 4) = 0, suy ra x = 0 hoặc x = 4.
Bước 4: Kiểm tra lại các nghiệm với phương trình ban đầu. Chỉ x = 4 là nghiệm của phương trình.
Khi giải phương trình chứa căn thức hoặc phân thức, cần đặc biệt chú ý đến điều kiện xác định của phương trình. Việc kiểm tra lại nghiệm sau khi giải là vô cùng quan trọng để đảm bảo tính chính xác của kết quả.
Để củng cố kiến thức, bạn có thể thực hành giải các bài tập sau:
Phương trình quy về phương trình bậc hai có nhiều ứng dụng trong thực tế, chẳng hạn như:
Lý thuyết Phương trình quy về phương trình bậc hai là một phần kiến thức cơ bản nhưng vô cùng quan trọng trong chương trình Toán 10. Việc nắm vững lý thuyết và rèn luyện kỹ năng giải bài tập sẽ giúp bạn tự tin hơn trong các kỳ thi và ứng dụng kiến thức vào thực tế.
Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn hiểu rõ hơn về chủ đề này. Chúc bạn học tập tốt!