Bài 9.21 trang 89 SGK Toán 10 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.21 này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ quá trình học tập của các em.
Gieo một đồng xu cân đối liên tiếp bốn lần. a) Vẽ sơ đồ hình cây mô tả không gian mẫu. b) Tính xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa.
Đề bài
Gieo một đồng xu cân đối liên tiếp bốn lần.
a) Vẽ sơ đồ hình cây mô tả không gian mẫu.
b) Tính xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa.
Lời giải chi tiết
a) Kí hiệu S là đồng xu ra mặt sấp và N là đồng xu ra mặt ngửa. Ta có sơ đồ cây:
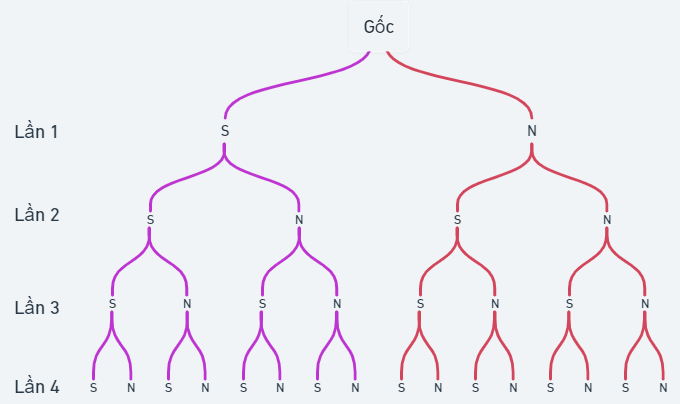
Dựa vào sơ đồ cây ta suy ra \(n\left( \Omega \right) = 16\).
b) Gọi A là biến cố: “Gieo đồng xu 4 lần có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”.
Suy ra A = {SSNN; SNSN; SNNS; NSSN; NSNS; NNSS}. Suy ra n(A) = 6. Vậy\(P\left( A \right) = \frac{6}{{16}} = \frac{3}{8}\).
Bài 9.21 SGK Toán 10 Kết nối tri thức yêu cầu chúng ta sử dụng kiến thức về tích vô hướng của hai vectơ để chứng minh một đẳng thức hình học. Để giải bài này một cách hiệu quả, chúng ta cần nắm vững định nghĩa tích vô hướng, các tính chất của tích vô hướng và cách áp dụng chúng vào việc giải quyết các bài toán liên quan đến vectơ.
Trước khi đi vào giải bài tập, hãy cùng ôn lại một số kiến thức lý thuyết quan trọng:
Bài 9.21 thường yêu cầu chứng minh một đẳng thức liên quan đến các vectơ trong một hình học cụ thể (ví dụ: tam giác, hình bình hành, hình chữ nhật). Để giải bài này, chúng ta thường sử dụng các bước sau:
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, giải thích rõ ràng và các phép tính chính xác. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu chứng minh \vec{AB} \cdot \vec{AC} = \frac{1}{2} (AB^2 + AC^2 - BC^2)".
Chúng ta sẽ sử dụng định lý cosin trong tam giác ABC: BC^2 = AB^2 + AC^2 - 2AB \cdot AC \cos(\angle BAC)".
Từ đó, ta có \cos(\angle BAC) = \frac{AB^2 + AC^2 - BC^2}{2AB \cdot AC}".
Sử dụng định nghĩa tích vô hướng, ta có \vec{AB} \cdot \vec{AC} = AB \cdot AC \cos(\angle BAC)".
Thay giá trị của \cos(\angle BAC)" vào, ta được \vec{AB} \cdot \vec{AC} = AB \cdot AC \cdot \frac{AB^2 + AC^2 - BC^2}{2AB \cdot AC} = \frac{1}{2} (AB^2 + AC^2 - BC^2)".
Vậy, đẳng thức được chứng minh.
Sau khi nắm vững lời giải của bài 9.21, các em có thể tự giải các bài tập tương tự để củng cố kiến thức. Một số bài tập gợi ý:
Bài 9.21 trang 89 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về tích vô hướng và ứng dụng của nó trong hình học. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.