Bài 6.23 trang 27 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.23 trang 27 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa điểm B. cách mình một đoạn 200m thì Minh bắt đầu đi bộ ra lề đường để bắt kịp xe.
Đề bài
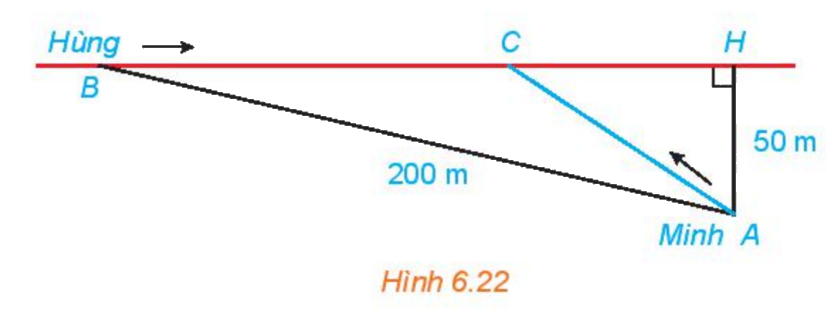
Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa điểm B. cách mình một đoạn 200m thì Minh bắt đầu đi bộ ra lề đường để bắt kịp xe. Vận tốc đi bộ của Minh là 5 km/h, vận tốc xe đạp của Hùng là 15 km/h. Hãy xác định vị trí C trên lề đường (H.6.22) để hai bằng gặp nhau mà không bạn nào phải chờ người kia (làm tròn kết quả đến hàng phần mười)
Phương pháp giải - Xem chi tiết
Bước 1: Đặt CH=x (km) (x>0)
Bước 2: Tính quãng đường Minh di chuyển, Hùng di chuyển
Bước 3: Để hai người không phải chờ nhau thì thời gian đi của 2 bạn phải bằng nhau nên ta lập được phương trình:
\(\frac{{\sqrt {0,0025 + {x^2}} }}{5} = \frac{{\sqrt {15} - 20x}}{{300}}\)
Giải phương trình tìm được x là tìm được vị trí điểm C
Lời giải chi tiết
Đổi: 200m=0,2 km
50m=0,05km
Đặt CH=x (km) (x>0)
Xét tam giác CHA vuông ở H, ta có:
\(C{A^2} = C{H^2} + A{H^2} = {x^2} + 0,0025\)
=> Quãng đường Minh di chuyển là \(CA = \sqrt {{x^2} + 0,0025} \)
Vận tốc đi bộ của Minh là 5km/h nên thời gian di chuyển của Minh là:
\(\frac{{\sqrt {{x^2} + 0,0025} }}{5}\) (giờ)
Xét tam giác AHB xuông tại H, ta có:
\(\begin{array}{l}H{B^2} = A{B^2} - A{H^2} = {(0,2)^2} - {(0,05)^2} = 0,0375\\ \Rightarrow HB = \frac{{\sqrt {15} }}{{20}}\end{array}\)
=> Quãng đường mà Hùng di chuyển là: \(BC = HB - HC = \frac{{\sqrt {15} }}{{20}} - x\)
Vận tốc đạp xe của Hùng là 15km/h nên thời gian di chuyển của Hùng là:
\(\frac{{\frac{{\sqrt {15} }}{{20}} - x}}{{15}} = \frac{{\sqrt {15} - 20x}}{{300}}\) (giờ)
Để hai bạn không phải chờ nhau thì:
\(\begin{array}{l}\frac{{\sqrt {{x^2} + 0,0025} }}{5} = \frac{{\sqrt {15} - 20x}}{{300}}\\ \Leftrightarrow 60\sqrt {{x^2} + 0,0025} = \sqrt {15} - 20x\end{array}\)
Bình phương hai vế của phương trình trên ta được:
\(\begin{array}{l}3600\left( {{x^2} + 0,0025} \right) = 15 - 40\sqrt {15} x + 400{x^2}\\ \Leftrightarrow 3200{x^2} + 40\sqrt {15} x - 6 = 0\end{array}\)
\( \Leftrightarrow x = \frac{{ - \sqrt {15} - 3\sqrt 7 }}{{160}}\) hoặc \(x = \frac{{ - \sqrt {15} + 3\sqrt 7 }}{{160}}\)
Thay lần lượt các giá trị này vào phương trình đầu, ta thấy cả 2 giá trị đều thỏa mãn
Do x>0 nên ta chọn \(x = \frac{{ - \sqrt {15} + 3\sqrt 7 }}{{160}}\)
\( \Rightarrow BC = BH - CH = \frac{{\sqrt {15} }}{{20}} - \frac{{ - \sqrt {15} + 3\sqrt 7 }}{{160}} \approx 0,1682(km) = 168,2(m)\)
Vậy vị trí C thỏa mãn đề bài là điểm cách B khoảng 168,2 m
Bài 6.23 thuộc chương trình học Toán 10 Kết nối tri thức, tập trung vào việc vận dụng kiến thức về vectơ để giải quyết các bài toán hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Để giải bài 6.23, chúng ta cần phân tích đề bài một cách cẩn thận và xác định các yếu tố quan trọng. Sau đó, áp dụng các kiến thức và công thức đã học để tìm ra lời giải chính xác.
Đề bài: (Giả sử đề bài cụ thể của bài 6.23 được đưa ra ở đây. Ví dụ: Cho tam giác ABC, tìm vectơ AB + AC)
Lời giải:
(Tiếp tục trình bày lời giải chi tiết, bao gồm các bước giải, công thức sử dụng và kết quả cuối cùng. Cần giải thích rõ ràng từng bước để học sinh dễ hiểu.)
Để giúp học sinh hiểu rõ hơn về cách giải bài 6.23, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập tương tự.
Ví dụ 1: (Đưa ra một ví dụ tương tự bài 6.23 và giải chi tiết)
Bài tập 1: (Đưa ra một bài tập tương tự bài 6.23 để học sinh tự luyện tập)
Kiến thức về vectơ và các phép toán vectơ có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, bao gồm vật lý, kỹ thuật, khoa học máy tính và kinh tế. Việc nắm vững kiến thức này sẽ giúp học sinh có lợi thế trong học tập và làm việc sau này.
Bài 6.23 trang 27 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và các phép toán vectơ. Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa, các em học sinh sẽ hiểu rõ hơn về bài tập này và có thể tự tin giải quyết các bài tập tương tự.