Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 1 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 1 trang 51 và 52, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các giải thích rõ ràng, giúp bạn hiểu được bản chất của vấn đề.
Cho hình thoi ABCD cới cạnh có độ dài bằng 1 và BAD = 120 Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ Trong hình 4.14a, hãy chỉ ra vectơ Với hai vectơ a, b cho trước, lấy một điểm A vẽ các vectơ
Cho hình thoi ABCD cới cạnh có độ dài bằng 1 và \(\widehat {BAD} = {120^o}\). Tính độ dài của các vectơ \(\overrightarrow {CB} + \overrightarrow {CD} ,\;\overrightarrow {DB} + \overrightarrow {CD} + \overrightarrow {BA} .\)
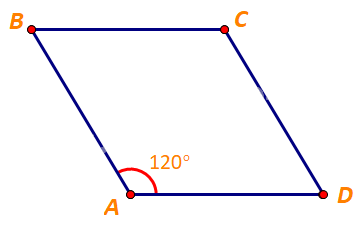
Lời giải chi tiết:
\(\overrightarrow {CD} = \overrightarrow {BA} \) do hai vectơ \(\overrightarrow {CD} ,\;\overrightarrow {BA} \) cùng hướng và \(CD = BA\).
\(\begin{array}{l} \Rightarrow \overrightarrow {CB} + \overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} \\ \Leftrightarrow \left| {\overrightarrow {CB} + \overrightarrow {CD} } \right| = \left| {\overrightarrow {CA} } \right| = CA\end{array}\)
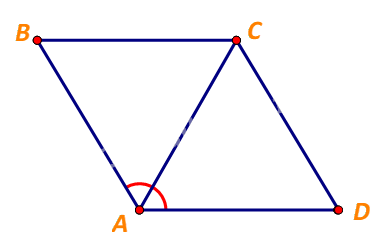
Xét tam giác ABC, ta có:
\(BA = BC\) và \(\widehat {BAC} = \frac{1}{2}.\widehat {BAD} = {60^o}\)
\( \Rightarrow \Delta ABC\) đều, hay \(CA = BC = 1\)
Vậy \(\left| {\overrightarrow {CB} + \overrightarrow {CD} } \right| = 1.\)
Dựa vào tính chất kết hợp, ta có:
\(\begin{array}{l}\overrightarrow {DB} + \overrightarrow {CD} + \overrightarrow {BA} = \left( {\overrightarrow {DB} + \overrightarrow {CD} } \right) + \overrightarrow {BA} \\ = \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right) + \overrightarrow {BA} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} .\\ \Rightarrow \left| {\overrightarrow {DB} + \overrightarrow {CD} + \overrightarrow {BA} } \right| = \left| {\overrightarrow {CA} } \right| = CA = 1.\end{array}\)
Với hai vectơ \(\overrightarrow a ,\overrightarrow b \) cho trước, lấy một điểm A vẽ các vectơ \(\overrightarrow {AB} = \overrightarrow a ,\;\overrightarrow {BC} = \overrightarrow b \). Lấy điểm A’ khác A và cũng vẽ các vectơ \(\overrightarrow {A'B'} = \overrightarrow a ,\;\overrightarrow {B'C'} = \overrightarrow b \). Hỏi hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {A'C'} \) có mối quan hệ gì?
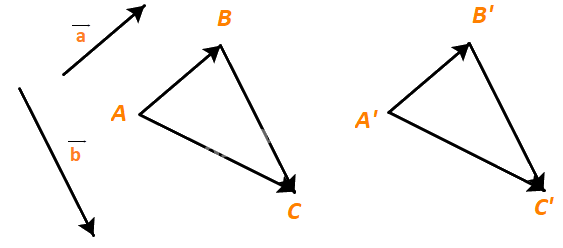
Phương pháp giải:
Hai vectơ bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Xét độ dài và hướng của hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {A'C'} \) để suy ra mối quan hệ của chúng.
Lời giải chi tiết:
\(\overrightarrow {AB} = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}AB//\;a\\AB = a\end{array} \right.\) và \(\overrightarrow {A'B'} = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}A'B'\;//\;a\\A'B' = a\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}AB//\;A'B'\\AB = A'B'\end{array} \right.\)
Tương tự, ta cũng suy ra \(\left\{ \begin{array}{l}BC//\;B'C'\\BC = B'C'\end{array} \right.\)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c-g-c)
\(\left\{ \begin{array}{l}AC//\;A'C'\\AC = A'C'\end{array} \right.\)
Dễ dàng suy ra \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \)
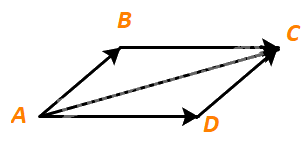
Phương pháp giải:
Bước 1: Xác định vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) bằng cách thay vectơ \(\overrightarrow {AD} \) bởi vectơ bằng nó mà có điểm đầu là B.
Bước 2: So sánh với vectơ \(\overrightarrow {AC} \)
Lời giải chi tiết:
Vì ABCD là hình bình hành nên \(\left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\), hay \(\overrightarrow {AD} = \overrightarrow {BC} \).
Do đó \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
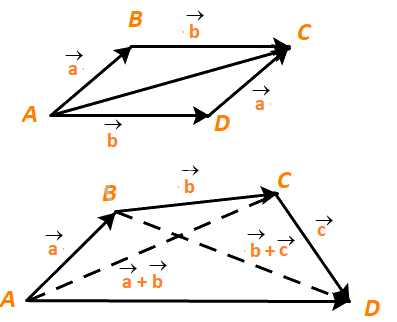
a) Trong hình 4.14a, hãy chỉ ra vectơ \(\overrightarrow a + \overrightarrow b \)và vectơ \(\overrightarrow b + \overrightarrow a \).
b) Trong hình 4.14b, hãy chỉ ra vectơ \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c \)và vectơ \(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\).
Phương pháp giải:
Nếu \(\overrightarrow {AB} = \overrightarrow a ,\;\overrightarrow {BC} = \overrightarrow b \) thì \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {AB} = \overrightarrow a ,\;\overrightarrow {BC} = \overrightarrow b \) nên \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Mặt khác: \(\overrightarrow {AD} = \overrightarrow b ,\;\overrightarrow {DC} = \overrightarrow a \) nên \(\overrightarrow b + \overrightarrow a = \overrightarrow {AD} + \overrightarrow {DC} = \overrightarrow {AC} \)
Do đó \(\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \).
b) Theo câu a) ta có \(\overrightarrow a + \overrightarrow b = \overrightarrow {AC} \) và \(\overrightarrow {CD} = \overrightarrow c \) nên \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \).
Mặt khác: \(\overrightarrow {BC} = \overrightarrow b ,\;\overrightarrow {CD} = \overrightarrow c \) nên \(\overrightarrow b + \overrightarrow c = \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {BD} \)
Và \(\overrightarrow a = \overrightarrow {AB} \) nên \(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
Vậy \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)
Với hai vectơ \(\overrightarrow a ,\overrightarrow b \) cho trước, lấy một điểm A vẽ các vectơ \(\overrightarrow {AB} = \overrightarrow a ,\;\overrightarrow {BC} = \overrightarrow b \). Lấy điểm A’ khác A và cũng vẽ các vectơ \(\overrightarrow {A'B'} = \overrightarrow a ,\;\overrightarrow {B'C'} = \overrightarrow b \). Hỏi hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {A'C'} \) có mối quan hệ gì?
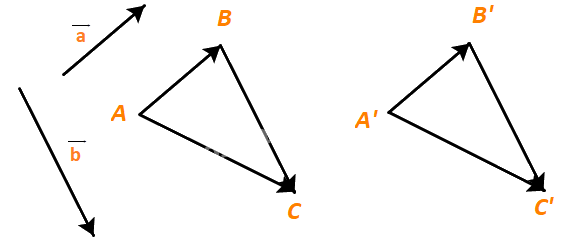
Phương pháp giải:
Hai vectơ bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Xét độ dài và hướng của hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {A'C'} \) để suy ra mối quan hệ của chúng.
Lời giải chi tiết:
\(\overrightarrow {AB} = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}AB//\;a\\AB = a\end{array} \right.\) và \(\overrightarrow {A'B'} = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}A'B'\;//\;a\\A'B' = a\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}AB//\;A'B'\\AB = A'B'\end{array} \right.\)
Tương tự, ta cũng suy ra \(\left\{ \begin{array}{l}BC//\;B'C'\\BC = B'C'\end{array} \right.\)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c-g-c)
\(\left\{ \begin{array}{l}AC//\;A'C'\\AC = A'C'\end{array} \right.\)
Dễ dàng suy ra \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \)
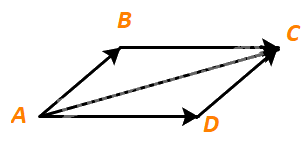
Phương pháp giải:
Bước 1: Xác định vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) bằng cách thay vectơ \(\overrightarrow {AD} \) bởi vectơ bằng nó mà có điểm đầu là B.
Bước 2: So sánh với vectơ \(\overrightarrow {AC} \)
Lời giải chi tiết:
Vì ABCD là hình bình hành nên \(\left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\), hay \(\overrightarrow {AD} = \overrightarrow {BC} \).
Do đó \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
a) Trong hình 4.14a, hãy chỉ ra vectơ \(\overrightarrow a + \overrightarrow b \)và vectơ \(\overrightarrow b + \overrightarrow a \).
b) Trong hình 4.14b, hãy chỉ ra vectơ \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c \)và vectơ \(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\).
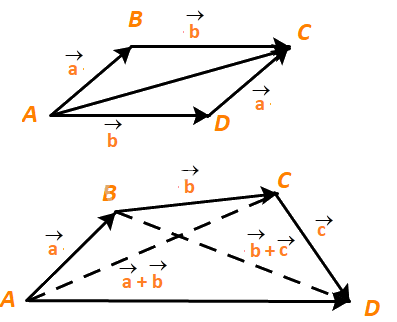
Phương pháp giải:
Nếu \(\overrightarrow {AB} = \overrightarrow a ,\;\overrightarrow {BC} = \overrightarrow b \) thì \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {AB} = \overrightarrow a ,\;\overrightarrow {BC} = \overrightarrow b \) nên \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Mặt khác: \(\overrightarrow {AD} = \overrightarrow b ,\;\overrightarrow {DC} = \overrightarrow a \) nên \(\overrightarrow b + \overrightarrow a = \overrightarrow {AD} + \overrightarrow {DC} = \overrightarrow {AC} \)
Do đó \(\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \).
b) Theo câu a) ta có \(\overrightarrow a + \overrightarrow b = \overrightarrow {AC} \) và \(\overrightarrow {CD} = \overrightarrow c \) nên \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \).
Mặt khác: \(\overrightarrow {BC} = \overrightarrow b ,\;\overrightarrow {CD} = \overrightarrow c \) nên \(\overrightarrow b + \overrightarrow c = \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {BD} \)
Và \(\overrightarrow a = \overrightarrow {AB} \) nên \(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
Vậy \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)
Cho hình thoi ABCD cới cạnh có độ dài bằng 1 và \(\widehat {BAD} = {120^o}\). Tính độ dài của các vectơ \(\overrightarrow {CB} + \overrightarrow {CD} ,\;\overrightarrow {DB} + \overrightarrow {CD} + \overrightarrow {BA} .\)
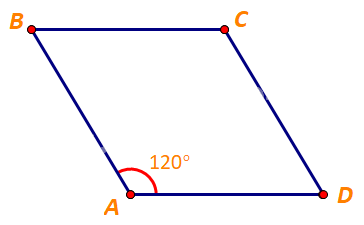
Lời giải chi tiết:
\(\overrightarrow {CD} = \overrightarrow {BA} \) do hai vectơ \(\overrightarrow {CD} ,\;\overrightarrow {BA} \) cùng hướng và \(CD = BA\).
\(\begin{array}{l} \Rightarrow \overrightarrow {CB} + \overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} \\ \Leftrightarrow \left| {\overrightarrow {CB} + \overrightarrow {CD} } \right| = \left| {\overrightarrow {CA} } \right| = CA\end{array}\)
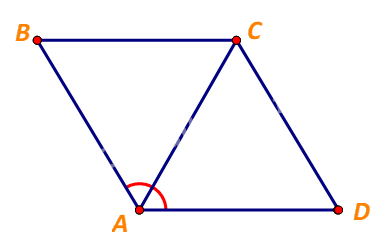
Xét tam giác ABC, ta có:
\(BA = BC\) và \(\widehat {BAC} = \frac{1}{2}.\widehat {BAD} = {60^o}\)
\( \Rightarrow \Delta ABC\) đều, hay \(CA = BC = 1\)
Vậy \(\left| {\overrightarrow {CB} + \overrightarrow {CD} } \right| = 1.\)
Dựa vào tính chất kết hợp, ta có:
\(\begin{array}{l}\overrightarrow {DB} + \overrightarrow {CD} + \overrightarrow {BA} = \left( {\overrightarrow {DB} + \overrightarrow {CD} } \right) + \overrightarrow {BA} \\ = \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right) + \overrightarrow {BA} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} .\\ \Rightarrow \left| {\overrightarrow {DB} + \overrightarrow {CD} + \overrightarrow {BA} } \right| = \left| {\overrightarrow {CA} } \right| = CA = 1.\end{array}\)
Mục 1 của chương trình Toán 10 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và mở rộng kiến thức về tập hợp, các phép toán trên tập hợp, và các khái niệm cơ bản về số thực. Việc nắm vững những kiến thức này là nền tảng quan trọng cho việc học các chương tiếp theo.
Mục 1 bao gồm các nội dung sau:
Để giải tốt các bài tập trong Mục 1, bạn cần:
(Đề bài: Liệt kê các phần tử của tập hợp A = {x | x là số tự nhiên nhỏ hơn 10})
Giải: Tập hợp A bao gồm các số tự nhiên nhỏ hơn 10, tức là A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
(Đề bài: Cho hai tập hợp B = {1, 2, 3} và C = {2, 4, 6}. Tìm B ∪ C và B ∩ C)
Giải:
(Đề bài: Giải bất đẳng thức 2x + 3 > 7)
Giải:
Vậy, nghiệm của bất đẳng thức là x > 2.
(Đề bài: Tìm giá trị tuyệt đối của -5 và 3)
Giải:
Hy vọng rằng với những giải thích chi tiết và phương pháp giải bài tập được trình bày ở trên, bạn sẽ tự tin hơn trong việc học Toán 10 tập 1 - Kết nối tri thức. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình. Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán!