Lý thuyết Hệ thức lượng trong tam giác là một phần quan trọng của chương trình Hình học lớp 10, cung cấp các công cụ mạnh mẽ để giải quyết các bài toán liên quan đến tam giác.
Tại giaitoan.edu.vn, chúng tôi cung cấp một lộ trình học tập bài bản, từ các định nghĩa cơ bản đến các ứng dụng nâng cao, giúp bạn nắm vững kiến thức một cách dễ dàng.
1. Định lí cosin 2. Định lí sin 3. Giải tam giác và ứng dụng thực tế
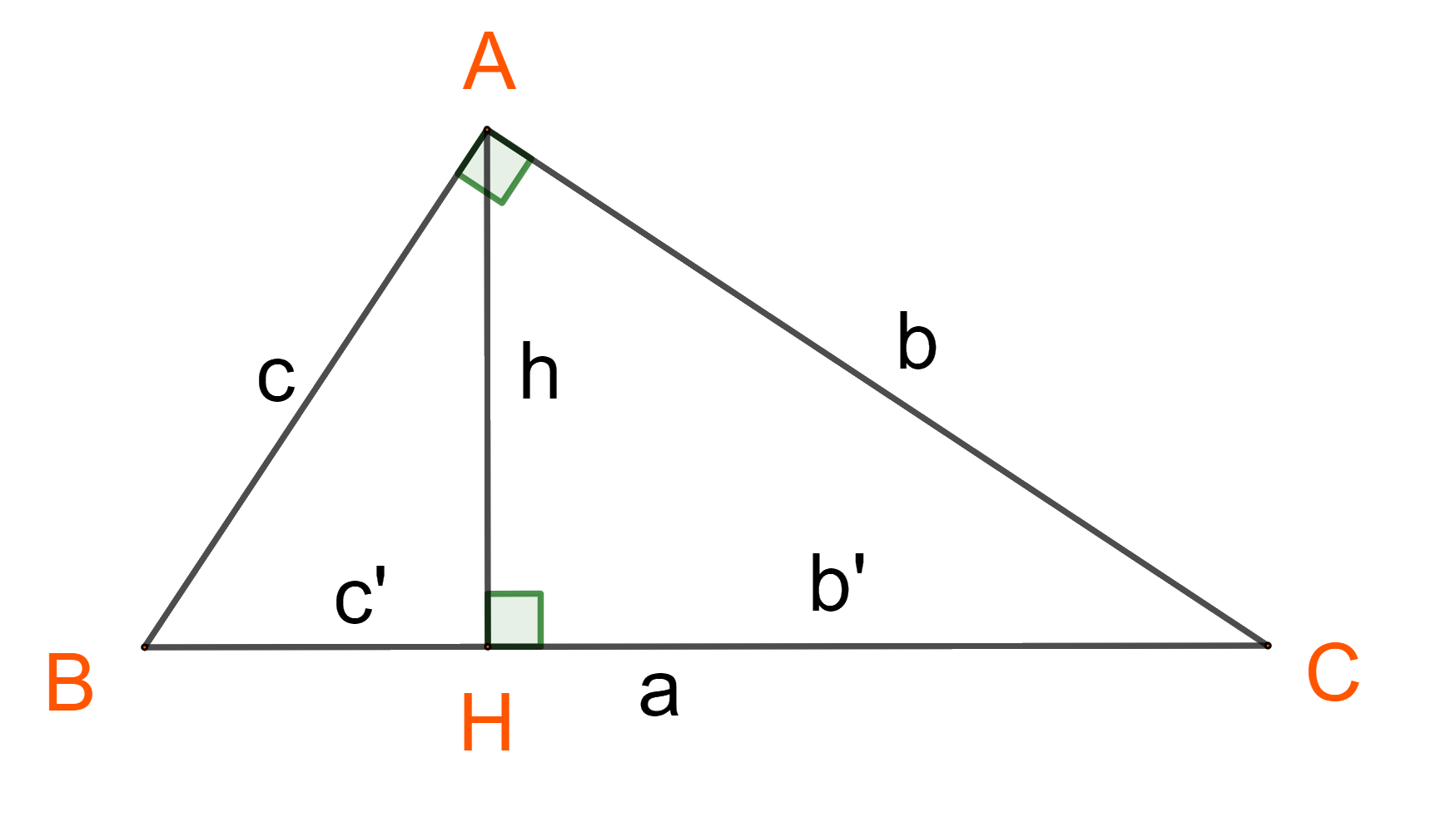
Nhắc lại hệ thức lượng trong tam giác vuông.
Cho tam giác \(ABC\) vuông góc tại đỉnh \(A\) (\(\widehat{A} = 90^0\)), ta có:
1. \({b^2} = ab';{c^2} = a.c'\)
2. Định lý Pitago : \({a^2} = {b^2} + {c^2}\)
3. \(a.h = b.c\)
4. \(h^2= b’.c’\)
5. \(\dfrac{1}{h^{2}}\) = \(\dfrac{1}{b^{2}}\) + \(\dfrac{1}{c^{2}}\)
1. Định lý cosin
Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với \(cosin\) của góc xen giữa chúng.
Ta có các hệ thức sau:
$$\eqalign{& {a^2} = {b^2} + {c^2} - 2bc.\cos A \, \, (1) \cr& {b^2} = {a^2} + {c^2} - 2ac.\cos B \, \, (2) \cr& {c^2} = {a^2} + {b^2} - 2ab.\cos C \, \, (3) \cr} $$
Hệ quả của định lí cosin:
\(\cos A = \dfrac{b^{2}+c^{2}-a^{2}}{2bc}\)
\(\cos B = \dfrac{a^{2}+c^{2}-b^{2}}{2ac}\)
\(\cos C = \dfrac{a^{2}+b^{2}-c^{2}}{2ab}\)
Áp dụng: Tính độ dài đường trung tuyến của tam giác:
Cho tam giác \(ABC\) có các cạnh \(BC = a, CA = b\) và \(AB = c\). Gọi \(m_a,m_b\) và \(m_c\) là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh \(A, B, C\) của tam giác. Ta có
\({m_{a}}^{2}\) = \(\dfrac{2.(b^{2}+c^{2})-a^{2}}{4}\)
\({m_{b}}^{2}\) = \(\dfrac{2.(a^{2}+c^{2})-b^{2}}{4}\)
\({m_{c}}^{2}\) = \(\dfrac{2.(a^{2}+b^{2})-c^{2}}{4}\)
2. Định lí sin
Định lí: Trong tam giác \(ABC\) bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là
\(\dfrac{a}{\sin A}= \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R\)
với \(R\) là bán kính đường tròn ngoại tiếp tam giác
Công thức tính diện tích tam giác
Diện tích \(S\) của tam giác \(ABC\) được tính theo một trong các công thức sau
\(S = \dfrac{1}{2} ab \sin C= \dfrac{1}{2} bc \sin A \) \(= \dfrac{1}{2}ca \sin B \, \,(1)\)
\(S = \dfrac{abc}{4R}\, \,(2)\)
\(S = pr\, \,(3)\)
\(S = \sqrt{p(p - a)(p - b)(p - c)}\) (công thức Hê - rông) \((4)\)
Trong đó:\(BC = a, CA = b\) và \(AB = c\); \(R, r\) là bán kính đường tròn ngoại tiếp, bk đường tròn nội tiếp và \(S\) là diện tích tam giác đó.
3. Giải tam giác và ứng dụng vào việc đo đạc
Giải tam giác : Giải tam giác là đi tìm các yếu tố (góc, cạnh) chưa biết của tam giác khi đã biết một số yếu tố của tam giác đó.
Muốn giải tam giác ta cần tìm mối liên hệ giữa các góc, cạnh đã cho với các góc, các cạnh chưa biết của tam giác thông qua các hệ thức đã được nêu trong định lí cosin, định lí sin và các công thức tính diện tích tam giác.
Các bài toán về giải tam giác: Có 3 bài toán cơ bản về gỉải tam giác:
a) Giải tam giác khi biết một cạnh và hai góc.
=> Dùng định lí sin để tính cạnh còn lại.
b) Giải tam giác khi biết hai cạnh và góc xen giữa
=> Dùng định lí cosin để tính cạnh thứ ba.
Sau đó dùng hệ quả của định lí cosin để tính góc.
c) Giải tam giác khi biết ba cạnh
Đối với bài toán này ta sử dụng hệ quả của định lí cosin để tính góc:
\(\cos A = \dfrac{b^{2}+c^{2}-a^{2}}{2bc}\)
\(\cos B = \dfrac{a^{2}+c^{2}-b^{2}}{2ac}\)
\(cos C = \dfrac{a^{2}+b^{2}-c^{2}}{2ab}\)
Chú ý:
1. Cần lưu ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài (tức là yếu tố góc không được quá 2)
2. Việc giải tam giác được sử dụng vào các bài toán thực tế, nhất là các bài toán đo đạc.
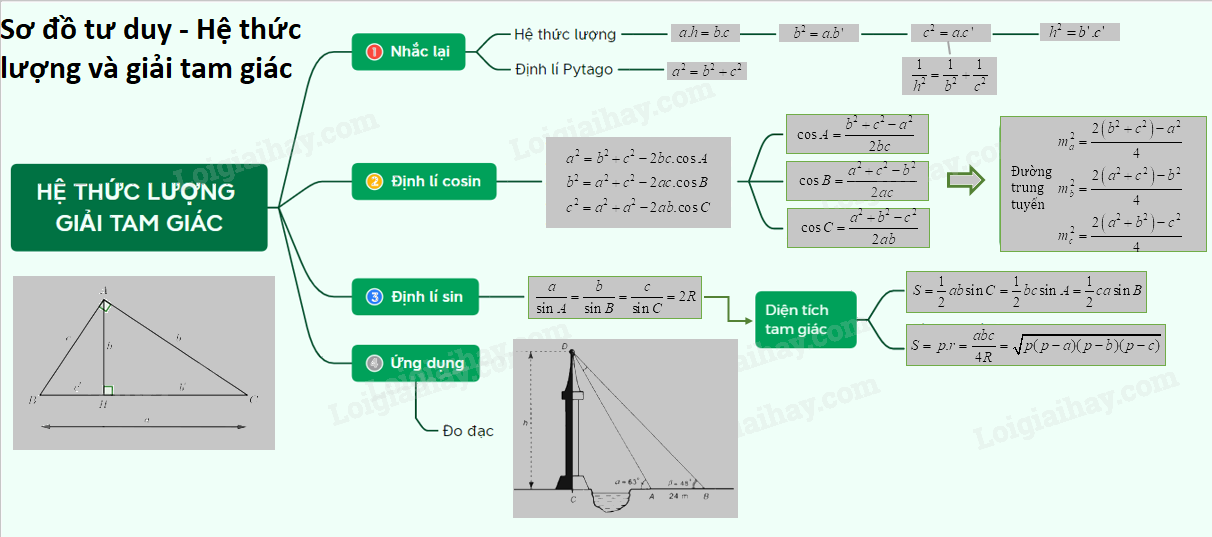
Lý thuyết Hệ thức lượng trong tam giác nghiên cứu mối quan hệ giữa các cạnh và các góc của một tam giác. Nó là nền tảng để giải quyết nhiều bài toán hình học phức tạp, đặc biệt trong các kỳ thi quan trọng như THPT Quốc gia.
Có ba hệ thức lượng cơ bản cần nắm vững:
Đối với tam giác thường, chúng ta có các hệ thức lượng sau:
Lý thuyết Hệ thức lượng có rất nhiều ứng dụng trong thực tế và trong các lĩnh vực khác của toán học:
Ví dụ 1: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính BC và sinB.
Giải:
Áp dụng định lý Pytago, ta có: BC2 = AB2 + AC2 = 32 + 42 = 25 => BC = 5cm.
sinB = AC/BC = 4/5 = 0.8
Ví dụ 2: Cho tam giác ABC có AB = 5cm, BC = 7cm, CA = 8cm. Tính góc A.
Giải:
Áp dụng định lý Cosin, ta có: BC2 = AB2 + CA2 - 2.AB.CA.cosA
=> 72 = 52 + 82 - 2.5.8.cosA
=> 49 = 25 + 64 - 80.cosA
=> cosA = (25 + 64 - 49)/80 = 40/80 = 0.5
=> A = 60o
Lý thuyết Hệ thức lượng trong tam giác là một công cụ quan trọng trong toán học. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết nhiều bài toán hình học một cách hiệu quả và tự tin. Hãy luyện tập thường xuyên và áp dụng kiến thức vào thực tế để đạt được kết quả tốt nhất.