Lý thuyết Nhị thức Newton là một trong những kiến thức quan trọng của chương trình Toán 10 Kết nối tri thức. Nó cung cấp công cụ mạnh mẽ để khai triển các biểu thức đại số, đặc biệt là các biểu thức có dạng (a + b)^n.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập vận dụng đa dạng, giúp bạn nắm vững lý thuyết và kỹ năng giải bài tập liên quan đến Nhị thức Newton.
1. Một số công thức khai triển
A. Lý thuyết
1. Một số công thức khai triển
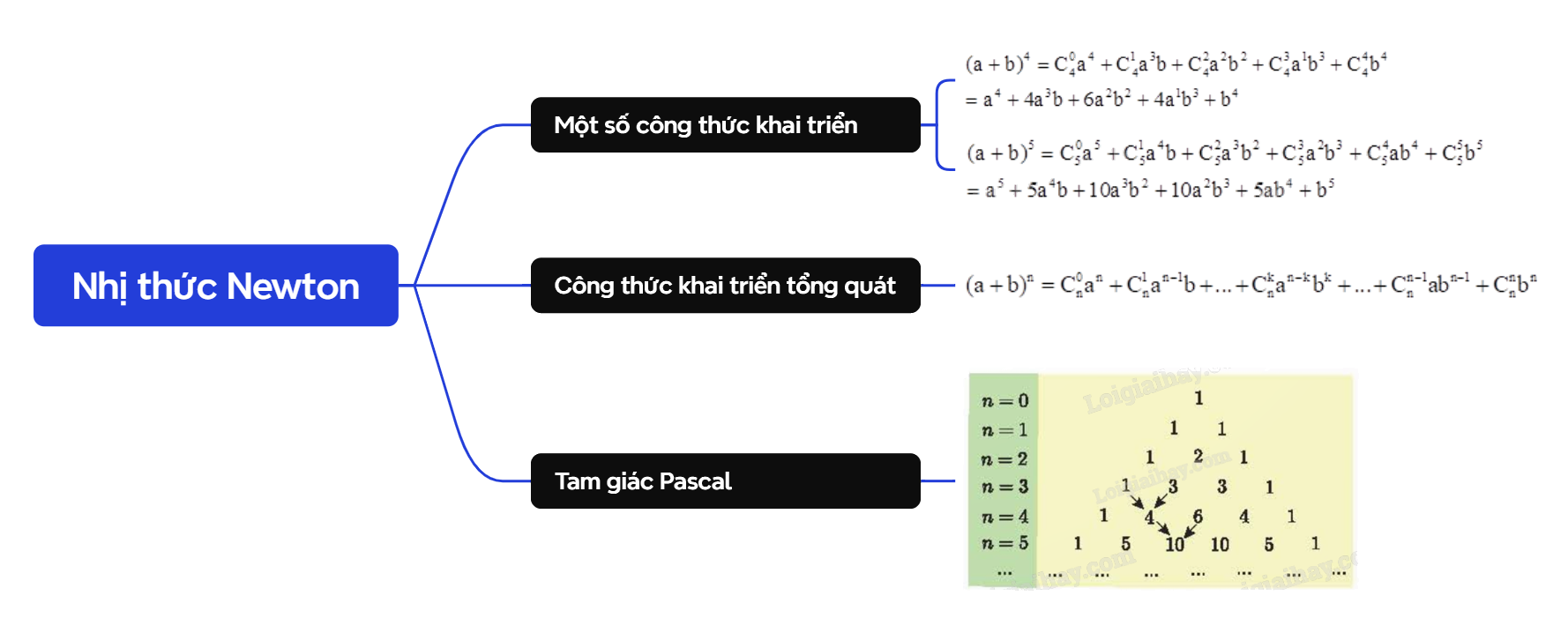
\({(a + b)^4} = C_4^0{a^4} + C_4^1{a^3}b + C_4^2{a^2}{b^2} + C_4^3{a^1}{b^3} + C_4^4{b^4} \) \(= {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4{a^1}{b^3} + {b^4}\). \({(a + b)^5} = C_5^0{a^5} + C_5^1{a^4}b + C_5^2{a^3}{b^2} + C_5^3{a^2}{b^3} + C_5^4a{b^4} + C_5^5{b^5}\) \( = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\). |
Những công thức khai triển nói trên là công thức nhị thức Newton \({(a + b)^n}\) ứng với n = 4 và n = 5.
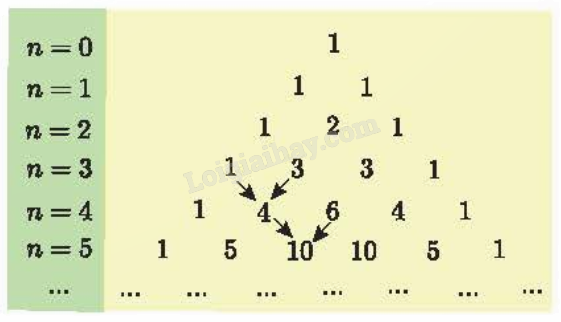
Chú ý: Các hệ số trong khai triển nhị thức Newton \({(a + b)^n}\) với n = 0; 1; 2; 3;… được viết thành từng hàng và xếp thành bảng số dưới đây. Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của hai số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũ tên trên bảng). Bảng số này được gọi là tam giác Pascal.
2. Công thức khai triển tổng quát
| \({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n - 1}}b + ... + C_n^k{a^{n - k}}{b^k} + ... + C_n^{n - 1}a{b^{n - 1}} + C_n^n{b^n}\). |
Nhận xét:
- Số hạng tổng quát trong khai triển của \({(a + b)^n}\) đều có dạng \(C_n^k{a^{n - k}}{b^k}\) \((0 \le k \le n)\).
- Từ công thức nhị thức Newton nói trên, ta có khai triển của \({(a - b)^n}\) như sau:
\({(a - b)^n} = C_n^0{a^n} - C_n^1{a^{n - 1}}b + C_n^2{a^{n - 2}}{b^2} - C_n^3{a^{n - 3}}{b^3} + ...\), ở đó các dấu “+”, “-“ xen kẽ nhau.
Ví dụ: \({(a - b)^3} = C_3^0{a^3} - C_3^1{a^{3 - 1}}b + C_3^2{a^{3 - 2}}{b^2} - C_3^3{a^{3 - 3}}{b^3}\)
\(= C_3^0{a^3} - C_3^1{a^2}b + C_3^2a{b^2} - C_3^3{b^3}\).
Có thể xem thêm trong Chuyên đề học tập Toán 10.
B. Bài tập
Bài 1: Khai triển biểu thức \({(x + 1)^4}\).
Giải:
Xác định số hạng: a = x, b = 1.
\({(x + 1)^4} = C_4^0{x^4} + C_4^1{x^3}.1 + C_4^2{x^2}{.1^2} + C_4^3{x^1}{.1^3} + C_4^4{.1^4} \)
\(= {a^4} + 4{x^3} + 6{x^2} + 4x + 1\).
Bài 2: Khai triển biểu thức \({(x - 1)^4}\).
Giải:
Có hai cách khai triển, tùy thuộc vào việc đặt b = -1 hay b = 1.
Nếu coi a = x, b = -1:
\({(x - 1)^4} = C_4^0{x^4} + C_4^1{x^3}.( - 1) + C_4^2{x^2}.{( - 1)^2} + C_4^3{x^1}.{( - 1)^3} + C_4^4.{( - 1)^4}\)
\(= {a^4} - 4{x^3} + 6{x^2} - 4x + 1\).
Hoặc có thể coi a = x, b = 1 và áp dụng công thức khai triển tổng quát:
\({(a - b)^n} = C_n^0{a^n} - C_n^1{a^{n - 1}}b + C_n^2{a^{n - 2}}{b^2} - C_n^3{a^{n - 3}}{b^3} + ...\), khi đó sẽ nhận được kết quả như trên (xen kẽ dấu).
Bài 3:
a) Khai triển biểu thức \({(x - 2y)^4}\) và tìm hệ số của số hạng chứa \({y^4}\).
b) Khai triển biểu thức \({(3x - y)^5}\).
Giải:
a) Coi a = x, b = -2y.
\({(x - 2y)^4} = {\left[ {x + ( - 2y)} \right]^4} = {x^4} + 4{x^3}( - 2y) + 6{x^2}{( - 2y)^2} + 4x{( - 2y)^3} + {( - 2y)^4}\)
\( = {x^4} - 8{x^3}y + 24{x^2}{y^2} - 32x{y^3} + 16{y^4}\).
Số hạng chứa \({y^4}\) là \(16{y^4}\), hệ số là 16.
b) Coi a = 3x, b = -y.
\({(3x - y)^5} = {\left[ {3x + ( - y)} \right]^5}\)
\( = {\left( {3x} \right)^5} + 5.{(3x)^4}.( - y) + 10{(3x)^3}.{( - y)^2} + 10{(3x)^2}.{( - y)^3} + 5.(3x).{( - y)^4} + {( - y)^5}\)
\( = 243{x^5} - 405{x^4}y + 270{x^3}{y^2} - 90{x^2}{y^3} + 15x{y^4} - {y^5}\).
Bài 4:
a) Xác định hệ số của \({x^6}\) trong khai triển \({\left( {2x + 1} \right)^{12}}\).
b) Xác định hệ số của \({x^9}\) trong khai triển \({\left( {3x - 2} \right)^{18}}\).
Giải:
a) Số hạng chứa \({x^6}\) là \(C_{12}^6.{\left( {2x} \right)^6} = C_{12}^6{.2^6}{x^6}\). Hệ số của \({x^6}\) là \(C_{12}^6{.2^6}\).
b) Số hạng chứa \({x^9}\) là \(C_{18}^9.{\left( {3x} \right)^9}.{( - 2)^9} = C_{18}^9.{( - 2)^9}{3^9}{x^9} = - C_{18}^9{.2^9}{3^9}{x^9}\). Hệ số của \({x^9}\) là \( - C_{18}^9{.2^9}{3^9} = - C_{18}^9{.6^9}\).
Bài 5: Cho tập hợp A = { a; b; c; d; e }. Tập hợp A có bao nhiêu tập hợp con?
Giải:
Tập hợp A có 5 phần tử. Mỗi tập con của A có k phần tử (1 ≤ k ≤ 5) là một tổ hợp chập k của A. Do đó, số tập con như vậy bằng \(C_5^k\). Mặt khác, có một tập con của A không có phần tử nào (tập rỗng), tức có \(C_5^0 = 1\) tập con như vậy. Do đó, số tập con của A bằng \(C_5^0 + C_5^1 + C_5^2 + C_5^3 + C_5^4 + C_5^5\). Theo công thức nhị thức Newton, ta có \(C_5^0 + C_5^1 + C_5^2 + C_5^3 + C_5^4 + C_5^5 = {(1 + 1)^5} = {2^5}\).
Vậy A có \({2^5} = 32\) tập con.
Lý thuyết Nhị thức Newton là một công cụ quan trọng trong đại số, cho phép chúng ta khai triển biểu thức (a + b)^n với n là một số nguyên dương. Nó có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật.
Hệ số nhị thức, ký hiệu là Ckn (đọc là "C k trên n"), được định nghĩa là số cách chọn k phần tử từ một tập hợp gồm n phần tử. Công thức tính hệ số nhị thức là:
Ckn = n! / (k! * (n - k)!)
Trong đó:
Công thức Nhị thức Newton phát biểu rằng:
(a + b)^n = Σnk=0 Ckn * an-k * bk
Trong đó:
Tam giác Pascal là một công cụ hữu ích để tính toán các hệ số nhị thức. Mỗi hàng của tam giác Pascal tương ứng với một giá trị của n, và các số trong hàng đó là các hệ số nhị thức Ckn với k từ 0 đến n.
Ví dụ:
| n | Hệ số nhị thức |
|---|---|
| 0 | C00 = 1 |
| 1 | C01 = 1, C11 = 1 |
| 2 | C02 = 1, C12 = 2, C22 = 1 |
| 3 | C03 = 1, C13 = 3, C23 = 3, C33 = 1 |
Nhị thức Newton có nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Ví dụ 1: Khai triển (x + 2)^3
(x + 2)^3 = C03 * x3 * 20 + C13 * x2 * 21 + C23 * x1 * 22 + C33 * x0 * 23
= 1 * x3 * 1 + 3 * x2 * 2 + 3 * x * 4 + 1 * 1 * 8
= x3 + 6x2 + 12x + 8
Ví dụ 2: Tìm hệ số của x2 trong khai triển (x - 1)^5
Hệ số của x2 là C35 * x2 * (-1)3 = 10 * x2 * (-1) = -10x2. Vậy hệ số của x2 là -10.
Khi áp dụng công thức Nhị thức Newton, cần lưu ý:
Hy vọng với những kiến thức và ví dụ trên, bạn đã hiểu rõ hơn về Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức này nhé!